Learn more: PMC Disclaimer | PMC Copyright Notice
Predicting Intra-Urban Variation in Air Pollution Concentrations with Complex Spatio-Temporal Dependencies
Abstract
We describe a methodology for assigning individual estimates of long-term average air pollution concentrations that accounts for a complex spatio-temporal correlation structure and can accommodate spatio-temporally misaligned observations. This methodology has been developed as part of the Multi-Ethnic Study of Atherosclerosis and Air Pollution (MESA Air), a prospective cohort study funded by the U.S. EPA to investigate the relationship between chronic exposure to air pollution and cardiovascular disease. Our hierarchical model decomposes the space-time field into a “mean” that includes dependence on covariates and spatially varying seasonal and long-term trends and a “residual” that accounts for spatially correlated deviations from the mean model. The model accommodates complex spatio-temporal patterns by characterizing the temporal trend at each location as a linear combination of empirically derived temporal basis functions, and embedding the spatial fields of coefficients for the basis functions in separate linear regression models with spatially correlated residuals (universal kriging). This approach allows us to implement a scalable single-stage estimation procedure that easily accommodates a significant number of missing observations at some monitoring locations. We apply the model to predict long-term average concentrations of oxides of nitrogen (NOx) from 2005–2007 in the Los Angeles area, based on data from 18 EPA Air Quality System regulatory monitors. The cross-validated R2 is 0.67. The MESA Air study is also collecting additional concentration data as part of a supplementary monitoring campaign. We describe the sampling plan and demonstrate in a simulation study that the additional data will contribute to improved predictions of long-term average concentrations.
1 Introduction
There is a growing understanding in the literature that exposure to air pollution is associated with adverse health outcomes. The early epidemiological evidence was based on assigning exposures using area-wide monitored concentrations in different geographic regions (Dockery et al. 1993; Pope et al. 2002) or at different times within the same region (Samet et al. 2000). A weakness of area-wide monitoring approaches is that they fail to take advantage of variation between individuals living in the same geographic region. In addition, depending on the study design, there is the potential for unmeasured confounding by region or by time.
More recent cohort studies have assigned individual concentrations based on estimates of intra-urban variations in ambient concentrations. Prediction approaches have included assigning the value measured at the nearest monitor to the participant’s residential location (Miller et al. 2007; Basu et al. 2000; Ritz et al. 2006); using “land use regression” estimates based on Geographic Information System (GIS) covariates (Hoek et al. 2008; Brauer et al. 2003; Jerrett et al. 2005a); and interpolating concentrations by a geostatistical method such as kriging (Jerrett et al. 2005b; Kunzli et al. 2005) or semi-parametric smoothing (Kunzli et al. 2005). These studies and others like them have used relatively simple spatial statistical techniques for exposure assignment based on monitoring data from existing regulatory networks. Our objective is a flexible and practical methodology that accounts for the complex structure of the ambient spatio-temporal concentration field and can take full advantage of regulatory and other monitoring data to more accurately predict concentrations for individual cohort members.
The work described in this paper is motivated by the Multi-Ethnic Study of Atherosclerosis and Air Pollution (MESA Air). MESA Air is a cohort study funded by the U.S. Environmental Protection Agency (EPA) that emphasizes accurate prediction of individual exposures in order to accomplish its primary aim of assessing the relationship between chronic exposure to air pollution and sub-clinical cardiovascular disease. The MESA Air cohort is comprised of 6226 male and female subjects in six major U.S. metropolitan areas (Los Angeles, CA; New York, NY; Chicago, IL; Minneapolis-St. Paul, MN; Winston-Salem, NC; and Baltimore, MD). Although it is possible to estimate health effects based on variations in concentrations between these regions, a major thrust in MESA Air is to develop accurate exposure predictions for individuals that also incorporate intra-urban difference in ambient concentrations in order to reduce exposure misclassification, increase the study power, and obviate possible confounding by region. The primary MESA Air hypotheses relate to exposure to particulate matter of ambient origin with aerodynamic diameter less than 2.5 µm (PM2.5). Gaseous oxides of nitrogen (NOx) demonstrate more intra-urban heterogeneity and are also considered as a marker for traffic-related air pollution. In this paper we present examples of modeling outdoor NOx concentrations in the Los Angeles area, but the statistical methodology is equally applicable to other regions and to PM2.5 and will ultimately be applied in all of these settings. We also note that final exposure estimates in MESA Air will integrate predictions of outdoor concentrations with additional subject-level data, including time-activity patterns, home infiltration characteristics, address history, and employment address.
A primary source of concentration data for estimating exposures is the EPA’s regulatory Air Quality System (AQS) repository of ambient monitoring data. The AQS network includes a number of fixed site monitors in each region, each of which measures ambient air pollution levels on a regular basis, typically hourly for NOx and less frequently for PM2.5. Although there are some missing data and variations between sites, most AQS sites provide nearly complete NOx concentration time series over several years at their spatial locations. MESA Air is also engaged in a supplementary measurement campaign to provide additional concentration data. The objective of the MESA Air monitoring is to more completely sample a design space that emphasizes traffic-related pollution and to capture data at actual subject home locations. For logistical reasons, the supplementary monitoring data are sampled as two-week averages based on a design with spatio-temporal misalignment that results in significant amounts of missing data at some measurement locations (Cohen et al. 2009).
Although the primary interest in MESA Air and similar cohort studies is in predicting spatial variation of long-term average concentrations to estimate exposures, our statistical modeling approach needs to account for spatio-temporal variability and correlation structures in the data. For an overview of techniques for modeling correlated spatio-temporal data, see Banerjee et al. (2004). A recent paper by Fanshawe et al. (2008) emphasizes the role of carefully chosen covariates in obviating the need to accommodate spatio-temporal correlation in the residuals, but the model in that paper assumes a uniform time trend across locations. Paciorek et al. (2008) and Sahu et al. (2006) model particulate matter using techniques that allow for more complex spatio-temporal dependencies, however their estimation and prediction procedures are applicable only with relatively well aligned monitoring data. Smith et al. (2003) uses an expectation-maximization (EM) algorithm to allow for arbitrary missing data patterns, but their model does not accommodate complex spatio-temporal dependencies. We describe a new modeling and prediction procedure that includes sufficiently complex spatio-temporal dependencies to accurately account for variation in seasonal patterns at different locations and that naturally allows for significant amounts of missing data.
In Section 2, we describe the available AQS monitoring data as well as the sampling pattern for the MESA Air supplementary monitoring campaign. We also describe the geographic covariates that are used in this paper. In Section 3, we specify our hierarchical spatio-temporal model and discuss techniques for efficient estimation. In Section 4, we apply the model to the AQS data from the Los Angeles region and assess the quality of predictions by cross-validation. In Section 5, we conduct a simulation study to assess the added benefit of including data from the supplementary MESA Air monitoring campaign. (The MESA Air supplementary monitoring campaign and quality control process are ongoing, so these concentration measurements are not included in the present paper.) We conclude in Section 6 with a discussion.
2 Description of Data
2.1 AQS Data
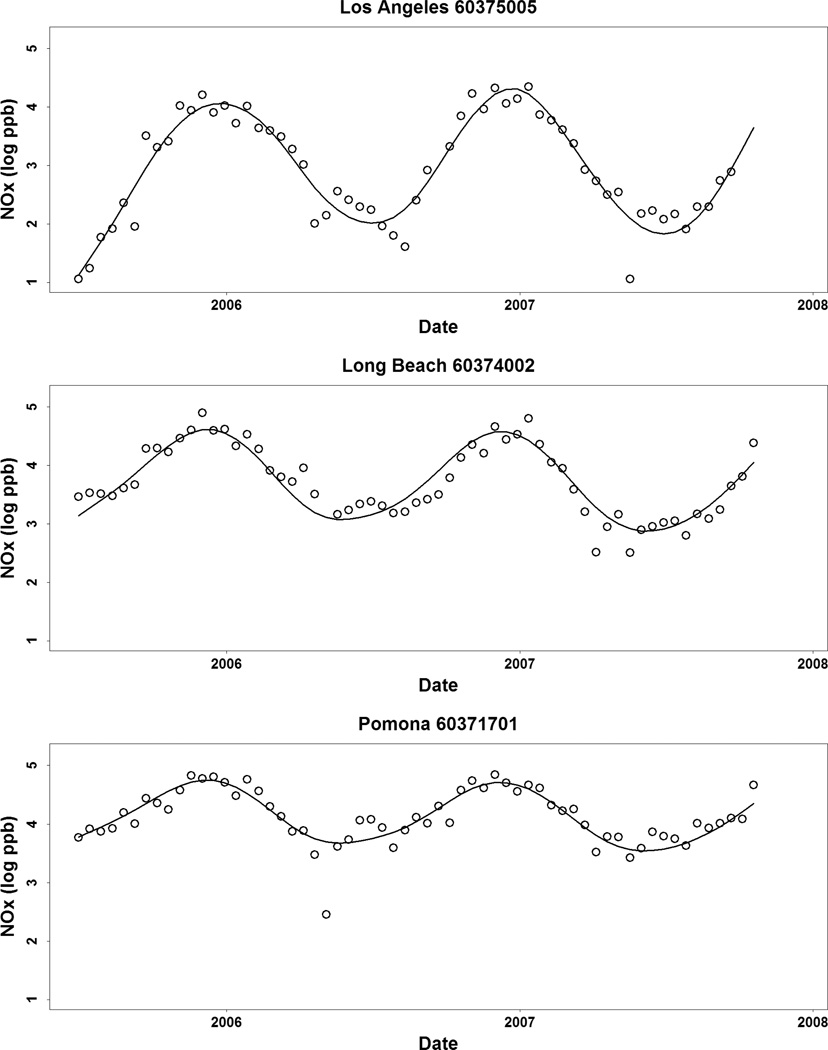
The EPA manages the national AQS network of regulatory monitors. Many AQS sites report NOx concentrations on an ongoing basis, most typically as hourly averages. For this study we are including data from 18 AQS monitors in the Los Angeles region that cover most of the area in which MESA Air cohort members reside. The monitor locations are shown on the map in Figure 1. Because the MESA Air supplementary monitoring is done at the two-week average time scale, we also aggregate the AQS monitoring data to two-week averages. There is a small amount of variability in the number of AQS measurements that contribute to each two-week average, which can result in variable amounts of measurement error. The current model assumes a common variance for the measurement error of all AQS and MESA Air two-week average concentrations. Since the data are skewed, we log-transform two-week average NOx concentrations. Example time series for the period from July 2005 through December 2007 are shown in Figure 2. The locations of these three sites in Los Angeles, Long Beach, and Pomona are highlighted on the map in Figure 1. Notice that the time series have different mean levels as well as different patterns of seasonal variation.
AQS and MESA Air monitoring locations in Los Angeles, and the 200 cohort residence locations used for validation in simulation scenario. (All home locations jittered on map to protect confidentiality)
2.2 MESA Air Monitoring
A major focus of the MESA Air project is to provide improved individual exposure prediction, relative to what has been used in previous air pollution cohort studies. To this end, additional monitoring data are being collected in each of the study’s six geographic regions. One of the problems with basing exposure estimates entirely on AQS monitoring data is that the AQS system is designed for regulatory rather than epidemiology study purposes. It is not intended to resolve small scale differences in pollution levels for individuals living in the same general area, and there are siting restrictions that limit the characterization of roadway effects on concentration levels. Therefore, the aim of the MESA Air supplementary monitoring campaign is to provide increased diversity in geographic sampling locations and to systematically span a design space based on proximity to traffic. In addition, the supplementary monitoring campaign involves collecting samples at a subset of the actual cohort home addresses (approximately one in ten cohort members) in order to more realistically characterize the pollution to which these cohort members are actually exposed. The sampling strategy and measurement methodology are described below and in more detail by Cohen et al. (2009).
The MESA Air supplementary monitoring for NOx in each of the six study areas involves collecting two-week average concentrations in three sub-campaigns: “fixed sites”, “home outdoor”, and “community snapshot”. All of the locations at which data had been collected in the Los Angeles region as of July 13, 2007 are shown on the map in Figure 1. Since the measurement and quality control processes are ongoing, measured concentrations are not used in the present paper, rather our simulation study is based on the actual locations and times of the MESA Air supplementary monitoring prior to July 13, 2007.
There are a total of seven MESA Air “fixed sites” in the Los Angeles area, one of which is colocated with an AQS monitor to allow for instrument calibration. These “fixed sites” began measuring two-week average concentrations in November 2005. There were approximately 40 measurements per site and a total of 264 “fixed site” measurements during this timeframe. A total of 73 “home outdoor” monitoring locations in Los Angeles are also included, and these were sampled during two-week periods starting in May 2006. The plan calls for each home to be sampled two times, in different seasons. As of the cutoff date for inclusion in this paper, a total of 103 “home outdoor” measurements were completed. The final component of supplemental monitoring is the “community snapshot” sub-campaign that consists of three separate rounds of spatially rich sampling during single two-week periods. In the downtown and coastal Los Angeles area, a total of 433 “community snapshot” measurements were made during three two-week periods in June 2006, October 2006, and January 2007. The sampling was done at different times in the Riverside area, with a total of 130 measurements from January 2007, April 2007, and June 2007. In each round of “community snapshot” monitoring, the majority of monitors were arranged in clusters of six, with three on either side of a major road at distances of approximately 50, 100, and 300 meters. In addition, the locations were chosen to characterize different land use categories and to cover the geographic region as broadly as possible.
2.3 Geographic Information System (GIS)
Part of our strategy for predicting concentrations at locations and times where there are no measurements is to use a regression model with geographic covariates. This approach is often termed “land use regression” because some of the geographic variables relate to local land utilization (Jerrett et al. 2005a). We embed this regression in a hierarchical spatio-temporal model that incorporates flexible correlation structures. In this paper, we consider a limited set of geographic covariates: (i) distance to the coast, (ii) distance to a major road (major road defined as census feature class code A1–A3, with distance truncated at 300 meters), and (iii) average population density in a 2000 meter buffer. These are all derived using the ArcGIS (ESRI, Redlands, CA) software package. The distance to coast variable is based on the Tele Atlas (Lebanon, NH) Dynamap 2000 County Boundary defined border of the Pacific Ocean, the population density is calculated from publicly available U.S. Census Bureau data, and the roadway variable is derived from the proprietary Tele Atlas Dynamap 2000 roadway network. The choice of these variables is based on preliminary exploratory analysis of the AQS monitoring data using linear regression (results not shown). In our final prediction model we plan to incorporate a much broader set of geographic covariates, including new covariates under development to account for local traffic patterns (Wilton et al. 2008).
3 Model and Estimation
3.1 Spatio-Temporal Framework
We are primarily interested in predicting long-term average concentrations at subject home locations, but certain features of the application and the data necessitate modeling the two-week average spatio-temporal field rather than pre-averaging the data for a purely spatial analysis. First, the long-term average time period of interest is not fixed, and it may vary between subjects based on the hypothesized time scale for the effect of air pollution exposure. We can easily accommodate the need for averages over arbitrary time periods by predicting a spatio-temporal field of two-week average concentrations.
Second, as we have seen in Figure 2, there are important spatio-temporal dependencies in the measured concentration field that manifest in varying seasonal patterns at different spatial locations. Given the spatio-temporal misalignment in the MESA Air supplementary monitoring, this suggests that we need to accurately account for space and time in order to optimally use these data. As a notional example, with only two concentration measurements at a particular home, the only way to determine if these data suggest that the home has long-term average concentrations that are relatively high or low compared to other locations in the same region is to calibrate the two measurements by comparing them to an estimate of the seasonal trend at the home location.
We define here the overall spatio-temporal modeling framework. Denote by Yst a set of known observations from a space-time field of log-transformed two-week average concentration measurements with indices st ∈ W, where the cardinality of W is
Define the set of all times at which there are measurements
the set of all locations at which there are measurements
and the total number of spatial locations
Also define the set of times for which there are measurements at location s ∈ S
and the set of locations for which there are measurements at time t ∈ T
Let be a set of values from the same space-time field at which we are interested in making predictions, and similarly define W*, N*, n*, T*, S*, , and . The space-time indices in Yst and may overlap, in which case the predicted value could differ from the colocated observations due to the potential for measurement error and process noise that we do not want to include in the health effect analysis.
We assume that Yst and can be modeled jointly as a Gaussian random field with a multi-dimensional parameter Ψ
Our strategy is to first estimate Ψ and then use the estimated along with the known values of Yst to predict . Specifically, we estimate Ψ by the method of maximum-likelihood
where the density for Yst is
In the above expression, ΣY (Ψ) and μY (Ψ) are sub-matrices of ΣYY* (Ψ) and μYY* (Ψ). We then predict as the conditional mean of from equation (1)
We can also compute uncertainty estimates for the that incorporate the covariance from equation (1) and the uncertainty in estimating Ψ. We do not present these here as they do not add any new insight over the cross-validatory assessments of prediction accuracy in Section 4 and because such individual uncertainty estimates are not helpful when using the predicted concentrations to estimate exposure in a health effects analysis; see the discussion in Section 6.
Suppose that we are interested in long-term average concentrations over a time interval (τ1, τ2) at a set of locations S*. We can obtain the spatial field of long-term average predictions by defining W* such that for each location s ∈ S*, consists of a non-overlapping sequence of two-week periods ranging from (τ1, τ2) and then computing the average back-transformed concentration
We have defined to average over the same time period at each location s, but this is only for notational convenience. In practice, we can easily predict averages over different time periods for different subjects’ home locations.
3.2 Hierarchical Model
We now describe the hierarchical structure for the multivariate Gaussian model in equation (1). To ease the notation we describe the model as it applies to Yst, but it is easy to expand it to the pair . We decompose the field into
where μst and νst will be defined below. The idea is that μst represents a smooth spatio-temporal mean field that incorporates dependence on geographic covariates along with seasonal and long-term trends, and νst represents the space-time residual field with primarily spatial correlation structure.
Take as given for now a set of m smooth temporal basis functions f1(t), …, fm(t), where m is typically a small number. We assume that each of the fi(t) has mean zero over the interval (τ1, τ2), and we also define the constant basis function f0(t) ≡ 1. Following Fuentes et al. (2006), we write the spatio-temporal mean field as
where for each i, we regard βi· as a spatial field on S of coefficients for fi(t). For each location s, the smooth function of time μs· represents the seasonal and long-term trend, which is essentially a projection of the time series at location s onto the space spanned by the fi(t).
Each of the spatial fields βi· is modeled by linear regression with geographic covariates and spatial correlation following a geostatistical structure, which amounts to embedding several instances of universal kriging (Cressie 1993) in our overall hierarchical model. In particular, we assume that for each i = 0, …, m
where Xi is an n × pi design matrix, αi is the corresponding pi-vector of unknown regression coefficients, and ΣS(θi) is obtained by plugging the unknown multi-dimensional parameter θi into a common n × n geostatistical covariance matrix function ΣS(·). Note that the design matrices Xi can incorporate intercept terms and may include different geographic covariates for the different spatial fields.
What remains is to specify a model for the residual space-time field νst. We will show (Section 4.1) that our modeling μst with seasonal basis functions leaves residuals that are essentially uncorrelated in time at the two-week average time scale. So we define νst as a mean-zero, separable space-time process, such that for each time t the spatial field ν·t is distributed as
and there is no temporal autocorrelation. The matrix function ΣSt(·) is defined to be the sub-matrix of ΣS(·) corresponding to the subset St ⊂ S, i.e., the set of locations with monitoring data at time t, and θν is a multi-dimensional geostatistical covariance parameter.
Notice that we have assumed a common family of spatial covariance functions for νst and the various spatial fields embedded in μst. We do this for notational convenience, but in practice it is not necessary. In particular, while we do not explore the possibility here, the residual field may have a non-stationary correlation structure that could be accommodated with a deformation model (Sampson 2002; Damian et al. 2003).
We still need to define the spatial covariance matrix function ΣS(·). Any of the common geostatistical forms would be appropriate, and the decision of which to use should be based on the data. In this paper, we focus on exponential covariance matrices that can be characterized by a range ϕ, partial sill σ2, and nugget τ2. For the βsi fields we assume that the nugget term is zero, implying that the mean value and seasonal trend are each highly correlated at adjacent locations. Thus, the parameter Ψ is composed of “land use regression” coefficients
along with spatial covariance parameters for the βsi fields
where
and spatial covariance parameters for the space-time residual field
The hierarchical model we have described in this subsection completely specifies the mean and covariance functions μY (Ψ) and ΣY (Ψ) of Section 3.1.
3.3 Unified Estimation
The first step in predicting is to find a parameter estimate by maximum-likelihood, as in equation (2). We use the constrained L-BFGS-B algorithm implemented in the optim() function in R (Byrd et al. 1995; R Development Core Team 2008), first log-transforming the variance parameters to make the optimization easier. The dimension of ΣY (Ψ) is N × N, where N is the total number of space-time concentration measurements in Yst. As such, the time consuming step in the optimization procedure is evaluating
For the simulation scenario we consider in Section 5 with n = 346 monitoring sites and a total of N = 2011 observations, one such evaluation takes 4.34 seconds running as a single thread in the default installation of R version 2.6.0 on a Dell workstation with two quad-core Intel Xeon processors running at 2.33 GHz processor (Red Hat Linux Enterprise Linux Server release 5.2, 64 bit). Linking R to the Goto implementation of a Basic Linear Algebra System (BLAS) in the identical setting reduces the computation time to 0.84 seconds (Goto 2008).
Although using R linked to the Goto BLAS results in reasonable computation times for our simulation scenario, we note that longer time series of measurements (which are available from the AQS monitors) would result in N being substantially larger than 2011, which could make direct evaluation of the term in (8) impractical on current generation computers. Fortunately an alternative method of calculating the likelihood is available that scales well for large N when the number of spatial locations n is held fixed.
We have already decomposed
To facilitate algebraic manipulations rewrite equation (9) in the form
with vectors Y = (Yst) and V = (νst) defined by varying s and then t, the vector B = (βis) defined by varying s and then i, and the matrix F = (fst,is′) with similar indexing defined by
We have
where ΣV is an N × N matrix with block diagonal structure, and we have
where
The likelihood for Y can be restated such that
where μB|Y and ΣB|Y are given by
This decomposition of the likelihood is convenient because the only N × N matrix to solve is ΣV, the covariance for the space-time residual field. This matrix is block-diagonal if we assume temporally uncorrelated residuals, and even if we were to assume an AR(1) or similar structure this matrix would be significantly more tractable than the full covariance ΣY. See Lindstrom and Lindgren (2008) for some related manipulations.
3.4 Temporal Basis Functions
Up to now we have regarded the fi(t) as pre-specified seasonal trend functions. In practice we follow an approach similar to Fuentes et al. (2006) and estimate empirical orthogonal basis functions from the data at locations where there are nearly complete time series for the dates of interest. If we restrict to the set of concentration measurements at such locations (e.g., the AQS sites) then we can regard Yst as a |T| × n matrix where T consists of a non-overlapping sequence of two-week periods ranging from (τ1, τ2) and n is the number of monitoring locations. For pre-specified m ≥ 1, if there were no missing data in Yst we would adopt the following procedure
- Construct Ỹst by normalizing the columns to have mean zero and variance one.
- Extract 1, …, m as the first m left singular vectors from a singular value decomposition (SVD) of Ỹst.
- Use smoothing splines to derive smooth temporal basis functions f1(t), …, fm(t) on the interval (τ1, τ2).
Recall that we always take f0(t) ≡ 1. The idea is that the first few singular vectors will span the range of seasonal trends observed in the data, but that they will be noisy representations so the smoothing is used to approximate the truly seasonal piece. Even the AQS time series have some missing values, so there are missing observations in Yst and the procedure described above cannot be applied directly. We modify step 2 of the procedure by using an algorithm similar to expectation-maximization (EM) to approximate the SVD using imputed values. See Fuentes et al. (2006) for further details on this algorithm.
4 Los Angeles AQS Data
We now apply the hierarchical model from Section 3 to make predictions based on two-week average log-transformed NOx concentrations from 18 monitoring locations of AQS network in the Los Angeles area for the time period from July 2005 through December 2007. This involves estimating the model parameters and then assessing prediction accuracy for long-term average concentrations by means of cross-validation. As previously noted, the locations of the monitors we consider are shown in Figure 1, and several example time series are shown in Figure 2.
Since there are essentially complete time series of data at each location, we can conduct a multistep exploratory analysis that will validate the appropriateness of the hierarchical model described in Section 3. This multi-step analysis gives estimates for all of the parameters in the hierarchical model, and we can compare these to the estimates obtained by the unified maximum-likelihood estimation procedure of Section 3.3.
4.1 Seasonal Trends and Residual Autocorrelation
We follow the methodology described in Section 3.4 to extract m = 2 smooth temporal basis functions that are intended to capture the range of seasonal variation in the region. After determining the first two singular vectors of the observed data matrix, we smooth them using smoothing splines as implemented in the R function smooth.spline() with four degrees of freedom per year (R Development Core Team 2008). The two seasonal trend functions are shown in Figure 3, and an additional basis function that is not shown is f0(t) ≡ 1. For each AQS monitoring location s, we estimate values 0s, 1s, and 2s by fitting
with ordinary least squares.
Smoothed (line) and unsmoothed (points) empirical orthogonal basis functions based on AQS NOx two-week averages in Los Angeles area (centered and normalized to SD=0.707 for smooth version).
For each location s, the residuals from this linear model constitute a time series. Our objective in using the basis functions to model seasonal variability is to simplify the structure of the residual field νst, ideally allowing us to treat it as having no temporal correlation. This corresponds to the residual time series being uncorrelated. Autocorrelation plots are shown in Figure 4 for the residuals at each of the 18 AQS sites. While there is a small amount of variability between sites, these plots taken as a group validate our assumption that there is no temporal correlation at the two-week time scale.
Empirical autocorrelation functions for two-week average residuals after fitting to empirical orthogonal basis functions. (18 AQS monitors in Los Angeles area.)
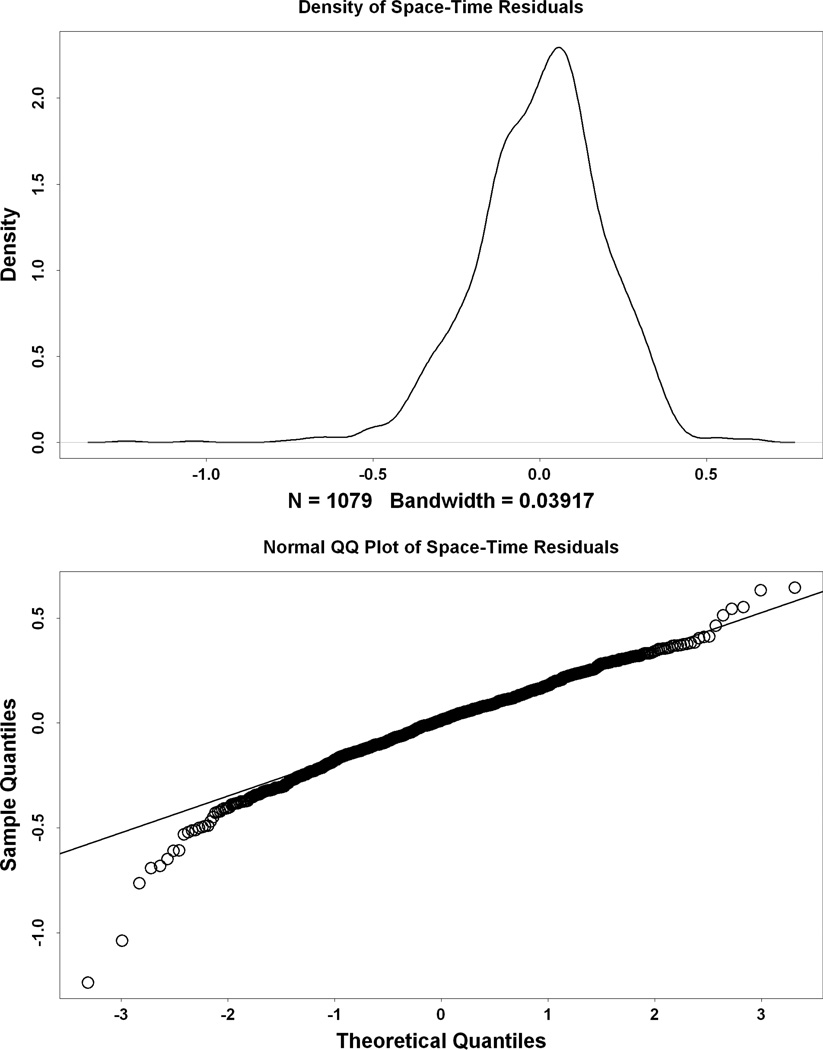
In order to assess the Normality assumption for the residual field, we show smoothed density and Normal Q-Q plots for the combined distribution of residuals from the 18 AQS sites in Figure 5. There is evidence of skewness in the distribution and a heavy left tail, but overall the Normality assumption seems like a reasonable approximation. In principle, our spatio-temporal model could be modified to make the residual distribution closer to Normal, potentially by using a generalized logarithm transformation (Durbin and Rocke 2003) or by formulating the model on a finer time scale (e.g., daily average concentrations). However, either of these approaches would entail a significant increase in the computational burden.
4.2 is Spatial Fields
For each i = 0, 1, 2 we analyze the estimated spatial field is in terms of its relationship with geographic covariates and its residual spatial structure. The three geographic covariates considered in this analysis are: (i) distance to the coast, (ii) distance to a major road (major road is defined by census feature class code A1–A3, with distance truncated at 300 meters), and (iii) average population density in a 2000 meter buffer. These variables were extracted using GIS, as described in Section 2.3.
The results of separate linear regression model fits for each of the is fields are shown in Table 1. As expected, the estimated long-term averages 0s tend to be lower for locations that are farther from roads and higher in areas of higher population density. In addition, the long-term averages tend to be higher further from the coast, which is broadly consistent with the notion that the prevailing wind concentrates pollution on the west side of the coastal mountains in the Los Angeles basin. The two sets of estimated seasonal basis function coefficients 1s and 2s do not have statistically significant relationships with the roadway or population variables, but both are associated with distance to the coast, indicating that the effect of meteorology varies by geography in this region.
Table 1
Linear regression parameter estimates (standard errors) for empirical orthogonal basis function coefficients of AQS monitors in Los Angeles area. Distance to nearest A1, A2, or A3 class road truncated at 300 meters. Population density based on a buffer with 2000 meter radius.
| β0 | β1 | β2 | ||||
|---|---|---|---|---|---|---|
| Intercept | 3.05 | (0.22) | 1.10 | (0.17) | −0.39 | (0.14) |
| Distance to road (km) | −1.37 | (0.57) | −0.62 | (0.43) | −0.19 | (0.35) |
| Distance to coast (km) | 0.012 | (0.003) | −0.009 | (0.002) | 0.006 | (0.002) |
| Population density (per m2) | 41.04 | (10.76) | −7.89 | (8.24) | 9.81 | (6.67) |
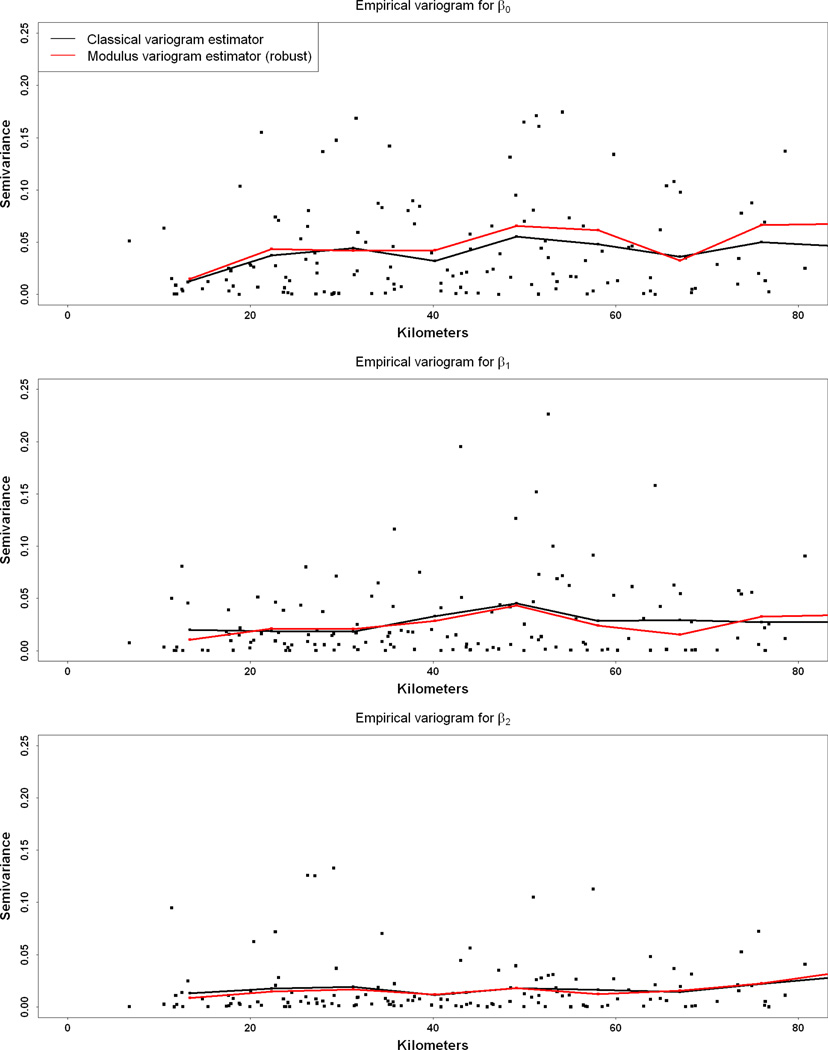
We expect there to be spatial correlation in the is fields. To assess the degree of spatial correlation, we examine empirical variograms for the residuals from regression on the spatial covariates. For 1s and 2s, only the distance to coast covariate is included in the regression since the other two covariates do not appear to be important. Empirical variogram clouds and binned values calculated using the GeoR package in R (Ribeiro and Diggle 2001) are shown in Figure 6. The variograms suggest that there is significant spatial correlation in 0s, modest correlation in 1s, but limited correlation in 2s. We quantify this by fitting universal kriging models with exponential variograms and no nugget to each of the three fields using the likfit() function in GeoR. The resulting parameter estimates are shown in the first column of Table 2.
Empirical variograms for the estimated spatial fields of long-term averages (0s) and coefficients of seasonal basis functions (1s, 2s). The black curve represents a classical variogram estimate, and the red curve is derived using the robust modulus method. (18 AQS monitors in Los Angeles area.)
Table 2
Hierarchical model parameter estimates for AQS data in Los Angeles area. The values in the first column are obtained by first estimating the βis at each site s and then fitting a universal kriging model to each estimated spatial field is. An estimated field of residuals st is then derived and fit to a separate ordinary kriging model to get the parameter estimates for ν. The values in the second column are obtained by a single step maximum-likelihood estimation for the full model as described in Section 3.3.
| Multi-step estimation | Full maximum-likelihood | |||||
|---|---|---|---|---|---|---|
| β0s | Intercept | 3.04 | 3.04 | |||
| Distance to road (km) | −1.63 | −1.62 | ||||
| Distance to coast (km) | 0.013 | 0.013 | ||||
| Population density (m−1) | 34.5 | 34.3 | ||||
| Sill | 0.049 | 0.049 | ||||
| Range (km) | 27.1 | 27.8 | ||||
| β1s | Intercept | 0.96 | 0.97 | |||
| Distance to coast (km) | −0.009 | −0.010 | ||||
| Sill | 0.031 | 0.032 | ||||
| Range (km) | 19.73 | 22.2 | ||||
| β2s | Intercept | −0.21 | −0.21 | |||
| Distance to coast (km) | 0.0052 | 0.0053 | ||||
| Sill | 0.017 | 0.017 | ||||
| Range (km) | 4.15 | 5.05 | ||||
| νst | Sill | 0.031 | 0.033 | |||
| Range (km) | 107.11 | 106.11 | ||||
| Nugget | 0.0095 | 0.0100 | ||||
4.3 Spatio-Temporal Residuals
The last part of the model to be estimated is the spatial structure of the spatio-temporal residual νst defined by equation (5). We can construct an estimate st by taking residuals from separately fitting the linear model in equation (12) at each location s. Then assuming an exponential form in equation (7) we jointly estimate the range, nugget, and sill parameters by maximum-likelihood using the likfit() function in GeoR. The estimated parameter values are shown in the first column of Table 2.
4.4 Full Model Estimation
In the previous subsections, we estimated the model parameters using a multi-step procedure. This is feasible for the AQS data because there are long time series with few missing values at each location, so it is possible to estimate the βis fields directly. If there were significant missing data (as in the MESA Air supplementary monitoring), it would be necessary to jointly estimate the model parameters using the full hierarchical form, and in any case a unified estimation procedure is preferable for estimating uncertainty in the health effect analyses (Szpiro et al. 2008; Gryparis et al. 2009; Madsen et al. 2008). Unified estimation of all of the parameters is accomplished by maximum-likelihood using the methodology describe in Section 3.3. Results for the AQS data are shown in the second column of Table 2, and there is very good agreement with estimates from the multi-step approach.
4.5 Prediction Accuracy
Using the parameter estimates derived above, it is straightforward to follow the procedure in Section 3.1 and predict long-term average concentrations at locations where measurements are not available. This amounts to predicting log-concentration values as the conditional mean of the latent Gaussian random field at locations without data, and then back-transforming to obtain concentrations as in equation (4).
We assess the accuracy of the prediction model by leave-one-out cross-validation. For each corresponding to the spatial location of one of the 18 AQS monitoring sites, we predict the long-term average concentration by applying the model from Section 3 as above, replacing Yst by the set of observations that excludes all measurements at location
This procedure yields a cross-validated spatial field of predicted long-term average concentrations , where s ranges over the 18 AQS monitoring locations. A scatter-plot of cross-validated pre-dictions is shown in Figure 7. The plot suggests that the model fits well since there are no noticeable outliers. The root mean square error (RMSE) is 4.21 parts per billion (ppb), corresponding to an R2 of 0.67. The formula used to compute R2 is
where is the spatial field of true long-term average concentrations that could be defined by replacing by in equation (4).
5 Simulation Study in Los Angeles
In order to evaluate the added value of the MESA Air supplementary monitoring campaign, we conducted a simulation study based on sampling Yst at all of the AQS and MESA Air sites described in Section 2 (N = 2011, n = 346). We simulated log-transformed two-week average concentrations using the hierarchical model of Section 3 with temporal basis functions and parameters as estimated from the AQS data in Section 4. We also simulated time series of concentrations at 200 additional randomly selected subject home addresses. The approximate locations are shown in Figure 1. We calculated the long-term average concentration values at each home address from July 2005 through December 2007 and regard these as a validation set for evaluating prediction performance.
We simulated 48 random realizations and then estimated the parameters using maximum-likelihood as in Section 3.3. Mean estimated parameter values are shown in the second column of Table 3 along with the standard deviation of estimates and the mean standard errors (calculated based on the Hessian of the likelihood function). The estimates are generally very close to the assumed values (first column), although we note that the range and sill tend to be underestimated for the β0s field. The sampling standard deviations are also reasonably well aligned with the standard error estimates. The standard errors are calculated by inverting the Hessian of the likelihood function at its mode. In future work, we will investigate alternative approaches such as Bayesian and empirical Bayesian calculations that may provide improved standard error estimates. The third column contains analogous values when the maximum-likelihood estimation is based only on simulated observations at the AQS and MESA Air “fixed sites” (N = 1343, n = 25). The mean values are very close to the ones obtained by using all monitoring locations, with a modest amount of additional variability. This suggests that the additional sampling at the “home outdoor” and “community snapshot” locations adds little value for parameter estimation.
Table 3
Mean, standard deviation, and expected standard errors of maximum-likelihood estimates of model parameters in 48 simulated realizations. The first column is the assumed values used to generate the data. The second column contains estimates based on values at all monitoring locations, and the third column contains estimates based on values at the AQS and MESA Air fixed sites only.
| Assumed values | ML with all locations | ML with AQS and fixed sites only | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | SD | E(SE) | Mean | SD | E(SE) | |||
| β0s | Intercept | 3.04 | 3.04 | 0.18 | 0.11 | 3.03 | 0.18 | 0.13 |
| Distance to road (km) | −1.62 | −1.62 | 0.049 | 0.046 | −1.64 | 0.21 | 0.22 | |
| Distance to coast (km) | 0.013 | 0.013 | 0.0037 | 0.0023 | 0.013 | 0.0039 | 0.0027 | |
| Population density (m−2) | 34.3 | 34.6 | 2.47 | 2.11 | 36.0 | 4.87 | 5.50 | |
| Log Sill | −3.02 | −3.61 | 0.50 | 0.39 | −3.71 | 0.54 | 0.42 | |
| Log Range (km) | 3.32 | 2.68 | 0.54 | 0.47 | 2.41 | 0.80 | 0.70 | |
| β1s | Intercept | 0.97 | 0.98 | 0.13 | 0.09 | 0.97 | 0.13 | 0.09 |
| Distance to coast (km) | −0.010 | −0.010 | 0.0024 | 0.0020 | −0.10 | 0.0025 | 0.0020 | |
| Log Sill | −3.45 | −3.88 | 0.36 | 0.38 | −3.94 | 0.35 | 0.40 | |
| Log Range (km) | 3.09 | 2.57 | 0.48 | 0.49 | 2.44 | 0.51 | 0.66 | |
| β2s | Intercept | −0.21 | −0.22 | 0.057 | 0.059 | −0.22 | 0.064 | 0.061 |
| Distance to coast (km) | 0.0053 | 0.0054 | 0.0013 | 0.0013 | 0.053 | 0.0016 | 0.0014 | |
| Log Sill | −4.07 | −4.13 | 0.23 | 0.27 | −4.22 | 0.31 | 0.33 | |
| Log Range (km) | 1.62 | 1.43 | 0.48 | 0.45 | 1.11 | 0.78 | 1.16 | |
| νst | Sill | −3.42 | −3.41 | 0.11 | 0.11 | −3.41 | 0.11 | 0.11 |
| Log Range (km) | 4.67 | 4.67 | 0.16 | 0.16 | 4.66 | 0.19 | 0.18 | |
| Log Nugget | −4.61 | −4.61 | 0.050 | 0.055 | −4.63 | 0.087 | 0.081 | |
However, our interest is in predicting the long-term average concentrations at subject home locations (), not just in estimating the model parameters. Scatterplots of predicted values for the first twelve Monte Carlo simulations in each of two scenarios are shown: (i) using the AQS and all MESA Air monitoring sites in Figure 8, and (ii) using only the AQS and MESA Air “fixed sites” in Figure 9. The predictions obtained by using information from all of the MESA Air monitoring sites are better than those using only the MESA Air “fixed sites”, with a lower average RMSE (4.02 compared to 6.24), and a higher average R2 (0.95 compare to 0.88). Since the parameter estimates are very close, this result suggests that there is significant benefit from having additional monitoring locations for the prediction step of equation (3), even though the measurements at the MESA Air “home outdoor” and “community snapshot” sites are temporally sparse.
Simulation study results for the first twelve Monte-Carlo realizations. Scatter plots of predicted vs. true long-term average NOx concentrations at 200 subject homes in validation set. Results based on using all AQS and MESA Air monitoring locations for parameter estimation and prediction.
Simulation study results for the first twelve Monte-Carlo realizations. Scatter plots of predicted vs. true long-term average NOx concentrations at 200 subject homes in validation set. Results based on using only AQS and MESA Air “fixed sites” for parameter estimation and prediction.
To further evaluate this potential benefit, we consider two additional prediction scenarios: (iii) all of the monitoring locations are used for parameter estimation but only the AQS and MESA Air “fixed sites” are used for prediction, and (iv) only the AQS and MESA Air “fixed sites” are used for parameter estimation but all of the monitoring locations are used for prediction. The results are shown in the red curves of Figures 10 and and11,11, and they validate the hypothesis that for this simulation scenario the primary benefit from including the “home outdoor” and “community snapshot” monitoring campaigns is for prediction rather than for parameter estimation. We also show analogous results for the incremental value of adding the “home outdoor” or “community snapshot” monitoring locations (green and blue curves, respectively, in Figures 10 and and11).11). The same pattern persists, with incremental benefit from each set of additional monitoring locations.
Simulation study results for 48 Monte-Carlo realizations. Average root mean squared error for predicted vs. true long-term average NOx concentrations at 200 subject homes in validation set. Results based on using different subsets of the AQS and MESA Air monitoring locations for parameter estimation and prediction in the spatio-temporal hierarchical model.
Simulation study results for 48 Monte-Carlo realizations. Average R2 for predicted vs. true long-term average NOx concentrations at 200 subject homes in validation set. Results based on using different subsets of the AQS and MESA Air monitoring locations for parameter estimation and prediction in the spatio-temporal hierarchical model. The formula used to compute R2 is given in Section 4.5.
We note that this simulation study demonstrates the benefit of having additional sampling from the “home outdoor” and “community snapshot” campaigns in the prediction step. In addition to the simulation study findings, there may turn out to be additional benefit for parameter estimation in the actual MESA Air study. This will be determined by the final choice of geographic covariates and how well the various sampling campaigns span the range of values for those covariates. The “community snapshot” campaign was specifically designed to capture near-road effects, and as we develop more refined traffic-related covariates we expect the data from this sub-campaign to be particularly important for estimating the relevant regression coefficients (Wilton et al. 2008).
In addition to the simulation scenario described above, we have also considered a second set of simulations in which we assume that there is greater variability in the temporal trend at a fine spatial scale. This additional variability is induced by allowing the β1s and β2s fields to be dependent on the distance to a major road covariate. The results are very similar, so we do not show them here.
6 Discussion
The methodology described in this paper has two features that make it attractive for exposure prediction in environmental epidemiology, and more generally for applications that benefit from accurate prediction using spatio-temporal data. First, our model has a very flexible correlation structure that allows for non-separability of space and time by modeling seasonal and long-term trends using empirical orthogonal basis functions with spatially correlated random fields of coefficients. Second, the unified estimation approach can be implemented with standard software and accommodates arbitrary missing data patterns, as long as there are sufficiently rich time series at a subset of locations to derive temporal basis functions.
An important consideration in implementing this model is determining what covariates are helpful for modeling the spatial fields of temporal basis function coefficients (recall that one of the temporal basis functions is the constant function, representing the long-term average). In this paper we have restricted our attention to a relatively small number of covariates that are easy to calculate using GIS. However, as part of our work on the MESA Air project, we are developing a more comprehensive set of spatial covariates, and we expect that these will be very valuable for making predictions at subject homes. In particular, we are investigating more complex covariates to account for the influence of local traffic patterns. This includes estimating actual traffic densities on the road network and incorporating the results of meteorology through physics-based plume modeling. Preliminary exploratory analysis in the Los Angeles region indicates that accounting for meteorology and traffic patterns will contribute significantly to improved predictions (Wilton et al. 2008).
One of our key findings in the simulation study is that the temporally sparse components of the MESA Air monitoring campaign (“home outdoor” and “community snapshot”) contribute to improved predictions, but that this improvement is primarily through better interpolation in the prediction step and not through improved parameter estimation. The details of this finding are likely connected to the choice of geographic covariates. For example, when we use more refined covariates to represent traffic density, we expect that the “community snapshot” monitoring will prove important for accurate estimation of the regression coefficients for these covariates. This is because the “community snapshot” monitoring includes extensive sampling at gradients within a few hundred meters of major roads in multiple directions corresponding to up- and down-wind locations. Thus, our expectation is that the benefit of MESA Air monitoring data in the prediction step will persist when we use additional covariates, and that additional gains in prediction accuracy will be realized through more accurate parameter estimation based on these data.
We have focused on making point predictions and evaluating the accuracy of these predictions compared to true values. It would be straightforward to also calculate a prediction variance at each location, taking a similar approach to Fanshawe et al. (2008). We do not pursue this here, however, because separate uncertainty estimates for each location are not helpful if the objective is to use the predicted concentrations to estimate the health effect in an environmental epidemiology study. To obtain valid health effect standard errors, we need to properly account for the uncertainty in the exposure prediction surface taken as a whole, including correlations between locations. In a future paper we will adapt recently developed measurement error correction procedures to accomplish this objective (Szpiro et al. 2008). Standard errors for the spatio-temporal model parameter estimates like those reported in Table 3 play an important role in the applicable measurement error correction procedures.
Footnotes
*Although the research described in this presentation has been funded wholly or in part by the United States Environmental Protection Agency through R831697 to the University of Washington, it has not been subjected to the Agency’s required peer and policy review and therefore does not necessarily reflect the views of the Agency and no official endorsement should be inferred.
References
- Banerjee S, Carlin BP, Gelfand AE. Hierarchical Modeling and Analysis for Spatial Data. Chapman and Hall: CRC; 2004. [Google Scholar]
- Basu R, Woodruff TJ, Parker JD, Saulnier L, Schoendorf KC. Particulate air pollution and mortality: Findings from 20 U.S. cities. New England Journal of Medicine. 2000;343(24):1742–1749. [PubMed] [Google Scholar]
- Brauer M, Hoek G, van Vliet P, Meliefste K, Fischer P, Gehring U, Heinrich J, Cyrys J, Bellander T, Lewne M, Brunekreef B. Estimating long-term average particulate air pollution concentrations: Application of traffic indicators and geographic information systems. Epidemiology. 2003;14(2):228–239. [PubMed] [Google Scholar]
- Byrd RH, Lu P, Nocedal J, Zhu C. A limited memory algorithm for bound constrained optimization. SIAM Journal on Scientific Computing. 1995;16:1190–1208. [Google Scholar]
- Cohen MA, Adar SD, Allen RW, Avol E, Curl CL, Gould T, Hardie D, Ho A, Kinney P, Larson TV, Sampson PD, Sheppard L, Stukovsky KD, Swan SS, Liu L-JS, Kaufman JD. Approach to estimating participant pollutant exposures in the Multi-Ethnic Study of Atherosclerosis and Air Pollution (MESA Air) Environmental Science and Technology. 2009 In Press. [PMC free article] [PubMed] [Google Scholar]
- Cressie NAC. Statistics for Spatial data. New York: John Wiley and Sons; 1993. [Google Scholar]
- Damian D, Sampson PD, Guttorp P. Variance modeling for nonstationary processes with temporal replications. Journal of Geophysical Research - Atmosphere. 2003;108(D24) [Google Scholar]
- Dockery DW, Pope CA, Xu X, Spangler JD, Ware JH, Fay ME, Ferris BG, Speizer FE. An association between air pollution and mortality in six cities. New England Journal of Medicine. 1993;329(24):1753–1759. [PubMed] [Google Scholar]
- Durbin B, Rocke DM. Estimation of transformation parameters for microarray data. Bioinformatics. 2003;19(11):1360–1367. [PubMed] [Google Scholar]
- Fanshawe TR, Diggle PJ, Rushton S, Sanderson R, Lurz PWW, Glinianaia SV, Pearce MS, Parker L, Charlton M, Pless-Mulloli T. Modelling spatio-temporal variation in exposure to particulate matter: a two-stage approach. Environmetrics. 2008;19(6):549–566. [Google Scholar]
- Fuentes M, Guttorp P, Sampson PD. Using transforms to analyze space-time processes. In: Finkenstadt B, Held L, Isham V, editors. Statistical Methods for Spatio-Temporal Systems. CRC/Chapman and Hall; 2006. pp. 77–150. [Google Scholar]
- Goto K. Gotoblas. 2008 http://www.tacc.utexas.edu/resources/software. [Google Scholar]
- Gryparis A, Paciorek CJ, Zeka A, Schwartz J, Coull BA. Measurement error caused by spatial misalignment in environmental epidemiology. Biostatistics. 2009;10(2):258. [PMC free article] [PubMed] [Google Scholar]
- Hoek G, Beelena R, de Hoogh K, Vienneaub D, Gulliverc J, Fischer P, Briggs D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmospheric Environment. 2008;42(3):7561–7578. [Google Scholar]
- Jerrett M, Arain A, Kanaroglou P, Beckerman B, Potoglou D, Sahsuvaroglu T, Morrison J, Giovis C. A review and evaluation of intraurban air pollution exposure models. Journal of Exposure Analysis and Environmental Epidemiology. 2005a;15:185–204. [PubMed] [Google Scholar]
- Jerrett M, Burnett RT, Ma R, Pope CA, Krewski D, Newbold KB, Thurston G, Shi Y, Finkelstein N, Calle EE, Thun MJ. Spatial analysis of air pollution mortality in Los Angeles. Epidemiology. 2005b;16(6):727–736. [PubMed] [Google Scholar]
- Kunzli N, Jerrett M, Mack WJ, Beckerman B, LaBree L, Gilliland F, Thomas D, Peters J, Hodis HN. Ambient air pollution and atherosclerosis in Los Angeles. Environmental Health Perspectives. 2005;113(2):201–206. [PMC free article] [PubMed] [Google Scholar]
- Lindstrom J, Lindgren F. A Gaussian Markov random field model for total yearly precipitation over the African Sahel. Lund University Mathematical Statistics Series. 2008 [Google Scholar]
- Madsen L, Ruppert D, Altman NS. Regression with spatially misaligned data. Environmetrics. 2008;19(5):453. [Google Scholar]
- Miller KA, Sicovick DS, Sheppard L, Shepherd K, Sullivan JH, Anderson GL, Kaufman JD. Long-term exposure to air pollution and incidence of cardiovascular events in women. New England Journal of Medicine. 2007;356(5):447–458. [PubMed] [Google Scholar]
- Paciorek CP, Yanosky JD, Suh HH. Practical large-scale spatio-temporal moeling of particulate matter concentrations. Harvard University Biostatistics Working Paper Series. 2008;(76) [Google Scholar]
- Pope CA, Burnett RT, Thun MJ, Calle EE, Ito K, Krewski D, Thurston GD. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution. Journal of the American Medical Association. 2002;9(287):1132–1141. [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2008. URL http://www.R-project.org ISBN 3-900051-07-0. [Google Scholar]
- Ribeiro PJ, Diggle PJ. geoR: A package for geostatistical analysis. 2001;1(2) [Google Scholar]
- Ritz B, Wilhelm M, Zhao Y. Air pollution and infant death in southern California, 19892000. Pediatrics. 2006;118(2):493–502. [PMC free article] [PubMed] [Google Scholar]
- Sahu SK, Gelfand AE, Holland DM. Spatio-temporal modeling of fine particulate matter. Journal of Agricultural, Biological, and Environmental Statistics. 2006;11(1):61–86. [Google Scholar]
- Samet JM, Dominici F, Curriero F, Coursac I, Zeger SL. Particulate air pollution and mortality: Findings from 20 U.S. cities. New England Journal of Medicine. 2000;343(24):1742–1749. [PubMed] [Google Scholar]
- Sampson PD. Spatial covariance. In: El-Shaarawi AH, Pierorcsh WW, editors. Encyclopedia of Environmetrics. ume 4. Wiley; 2002. pp. 2059–2067. [Google Scholar]
- Smith RL, Kolenikov S, Cox LH. Spatio-temporal modeling of pm2.5 data with missing values. Journal of Geophysical Research. 2003;108(D24):9004. [Google Scholar]
- Szpiro A, Sheppard L, Lumley T. Accounting for errors from predicting exposures in environmental epidemiology and environmental statistics. UW Biostatistics Working Paper Series. 2008 (Working Paper 330) [Google Scholar]
- Wilton D, Larson T, Gould T, Szpiro A. Including Caline3 dispersion model predictions into a land use regression model for NOx in Los Angeles, California and Seattle, Washington; In ISEE/ISEA Conference; 2008. [Google Scholar]