Have you noticed that the Internet can seem slow? Sometimes it takes a long time for web pages to load. It would really be better if they would just snap up instantly on the screen.

In practice, “instant” response occurs if the latency is less than ~1/30th of a second, or ~30 msec. Animation at thirty frames per second looks smooth. Only a small minority of the population has the retinal read-out frequency required to see that the Crab pulsar is flashing at 33.5 msec intervals.

Coincidently, the speed-of-light travel time along the (almost entirely overland) great circle route between Tokyo and New York is (to within a millisecond) the same as the Crab Pulsar’s current spin period. In theory, it should possible to load Japanese-sourced web pages with barely perceptible latency, as the service of a request involves a round-trip.

The fastest communication between Japan and the West Coast of the United States is via NTT’s PC-1 cable, which runs between cable landings at Ajigaura (near Tokyo) and Harbour Pointe (near Seattle). Round-trip communication on the cable takes 80 msec, which, given that the speed of light in optical fiber is ~1.44x slower than the speed of light in vacuum, indicates that cable must adhere fairly closely to the great circle route beneath the Pacific.

Here’s an interesting paper by Ankit Singla and his collaborators which explores the various drag terms that keep the Internet from actually running at the speed of light. As part of their research, they report on 20+ million measurements of 28,000 web urls served from 120+ countries. The cumulative distribution function of all that pinging points to a median latency for loading html that is ~40x slower than if the message was covering the inferred great circle distance at the speed of light in vacuum.

Singla et al. argue that the speed doesn’t have to be so slow:

A parallel low-latency infrastructure: Most flows on the Internet are small in size, with most of the bytes being carried in a small fraction of flows. Thus, it is conceivable that we could improve latency for the large fraction of small-sized flows by building a separate low-latency low-bandwidth infrastructure to support them. Such a network could connect major cities along the shortest paths on the Earth’s surface (at least within the continents) using a c-speed medium, such as either microwave or potentially hollow fiber. Such a vision may not be far-fetched on the time horizon of a decade or two.

Even a decade might be an overestimate. As oklo.org readers know, during the past several years, a secretive fleet of microwave networks have sprung up to transfer information between the Chicago and New York metro areas at as close to the speed of light as possible. The fastest of these networks now transmit within ~2% of the physical minimum. Tremendous efforts have gone into squeezing out every last source of delay.

It’s thus interesting to look at what a national low-latency microwave backbone might look like. To optimize on costs, and to minimize connection times, one wishes to connect a number of nodes (metropolitan areas) with the minimal complement of route segments. This task, known as the Steiner tree problem has an interesting history, and computationally, is non-deterministic polynomial-time (NP) hard. One can get analog solutions by placing a board with pegs representing the nodes into soapy water. The connective soap bubble films are physical representations of the Steiner trees:

I coded up a Steiner tree finder using an incremental optimization algorithm, and ran it on the top 20 metro areas in the US by populations, which (ranked according to distance from their centroid) are:

1 DFW
2 MSP
3 ORD
4 IAH
5 DIA
6 ATL
7 COL
8 DTW
9 DCA
10 PHX
11 TPA
12 PHL
13 NYC
14 MIA
15 SAN
16 LAX
17 BOS
18 SFO
19 PDX
20 SEA

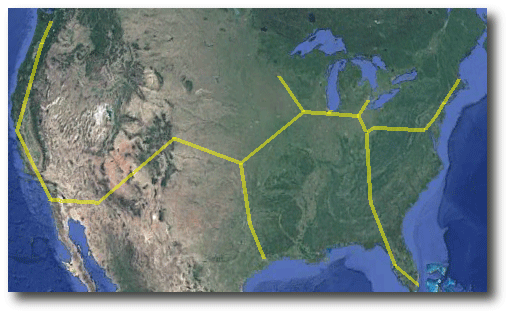
The algorithm, which employs the Vicenty distance formula between points on the Earth’s surface, and which is not guaranteed to find the absolute shortest route, links the 20 cities with a total path length of 9,814km, about 10x the length of a NYC-CHI route:

The added interconnecting nodes on the tree are the Steiner points. A prominent example on the map above connects Dallas and Denver with the Minneapolis-Chicago interconnect point, and lies in an obscure field a few miles south of Haven, Kansas.

Remarkably, when one zooms in on the exact spot, and settles into street view, there’s a red and white microwave tower a hundred meters or so from the actual Steiner point.

Rather fittingly, the tower has three dishes, indeed, pre-aligned and pointing in what appears to be the requisite directions…

The Gaia hypothesis, was introduced by James Lovelock in the 1970s and “proposes that organisms interact with their inorganic surroundings on Earth to form a self-regulating, complex system that contributes to maintaining the conditions for life on the planet.”

As the planet wires itself and its computers ever more tightly together in an ever-lower latency web of radio links and optical fiber, it no longer seems like a particular stretch to float an Electra hypothesis in which computational nodes and their interconnections assume a global role comparable to that now filled by the biological organisms.

In looking through oklo’s activity logs, it is evident that many of the visitors are not from the audience that I have in mind as I write the posts. The site is continually accessed from every corner of the planet by robots, harvesters, spamdexing scripts, and viral entities that attempt to lodge links into the blog.

A common strategy consists of attempts to ingratiate with generically vague comments of praise:

The Turing test was envisioned as a text-only conversation with a machine. The machine passes the test if it can’t be distinguished from a real person. In Alan Turning’s Computing Machinery and Intelligence, he asks, “Are there imaginable digital computers which could do well in the imitation game?”

For now, the general consensus seems to be no. Machines can’t consistently pass the test (and the test itself seems increasingly dated), but their moment is approaching fast. Judith Newman’s recent NYT article about interaction with the iPhone’s Siri telegraphs the stirrings of the current zeitgeist.

The economics of comment spam must be relatively minor. Were serious money was at stake, a Nice Post! robot armed with state-of-the-art-2015 natural language processing skills and tuned to the universe of text strings and facts could almost certainly pull the wool over my eyes.

In early 2001, I was working at NASA Ames Research Center. The first Internet Bubble hadn’t quite ended. Highway 101 was a near-continual traffic jam. Narrow billboard trucks advertising this or that dot com were still cycling aimlessly up and down the Peninsula. We had just published our plan to move the Earth in response to the gradually brightening Sun.

I got an e-mail with a stanford.edu address from someone named John McCarthy, who asked if he could come to NASA Ames to talk with us about astronomical engineering. This was before the Wikipedia, and for me, at least, before the ingrained reflex to turn to the web for information about someone one doesn’t know. I just wrote back, “Sure!”

I recall McCarthy in person as a rather singular character, with a bushy white beard surrounding thick black glasses. He had a rattletrap car with a bulky computer-like device somehow attached next to the steering wheel. My co-author, Don Korycansky, was there. I remember that the conversation was completely focused on the details of the orbits and the energy budgets that would be required. We didn’t engage in any of the far-out speculations or wide-eyed ramifications that thrust us, as a result of my ill-advised conversation with a reporter a few weeks later, into a terrifying worldwide media farce.

Only later did I realize that John McCarthy was one of the founding giants of computer science. He coined the term Artificial Intelligence, invented Lisp, and was famous for his Usenet .sig, “He who refuses to do arithmetic is doomed to talk nonsense.”

McCarthy’s Progress and Sustainability web pages (online at http://www-formal.stanford.edu/jmc/progress/index.html) are dedicated to the thesis of optimism — that human progress is desirable and sustainable. He wrote, “There are no apparent obstacles even to billion year sustainability.” In essence, the argument is that the Anthropocene epoch, which began at 05:29:21 MWT on July 16, 1945, will stretch to become an eon on par in duration with the Archean or the Proterozoic.

Optimistic is definitely the operative word. It’s also possible that the computational innovations that McCarthy had a hand in ushering in will consign the Anthropocene epoch to be the shortest — rather than one of the longest — periods in Earth’s geological history. Hazarding a guess, the Anthropocene might end not with the bang with which it began, but rather with the seemingly far more mundane moment when it is no longer possible to draw a distinction between the real visitors and the machine visitors to a web site.