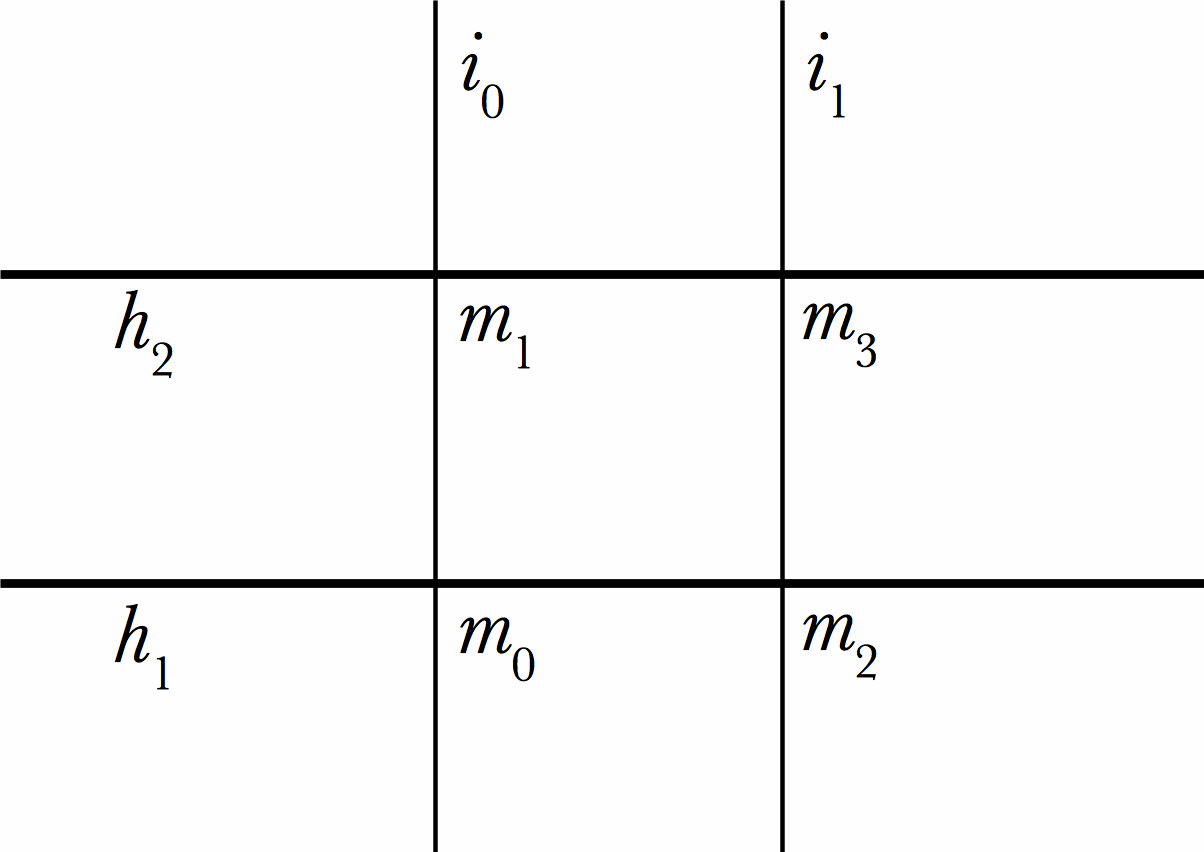Future Contingents

The riddle of the future bewilders human beings. On the one hand, we are inclined to think that future events are real in some sense, because we ask questions and make assertions about them. On the other hand, we are inclined to think that future events may depend on our choices, because we conceive of ourselves as free agents. These two inclinations seem to clash. If an event belongs to the future, then it is a fact that it will occur, and we cannot prevent it from occurring. Inversely, if we can prevent an event from occurring, then it cannot be a fact that it will occur. This apparent conflict is at the core of the debate on future contingents, a philosophical dispute that goes back to antiquity. Future contingents are sentences that concern future events that can occur or not occur. The question that started the debate—whether future contingents are true or false—is a question that has no clear answer, given that one may have different views about the truth and falsity of a sentence about the future. Yet an answer must be provided, and it cannot be just any answer. The constraints that define the problem of future contingents determine a restricted set of admissible answers, each of which gives rise to doubts, troubles, and complications.

The Problem
Three Logical Options
Three Metaphysical Views
The Open Future
References and Further Reading

1. The Problem

a. Speaking about the Future

Tomorrow many things will happen. Some of them are things of which it seems correct to assert that they will happen, others are things of which it does not seem correct to assert that they will happen. For example, it seems correct to assert that the sun will rise. Alternatively, it does not seem correct to assert that exactly 3,245 pigeons will walk in Piazza San Marco.

The reason why in certain cases it seems correct to assert that things will go a certain way is that in those cases we take it to be true that things will go that way. As far as we know, the sun will rise tomorrow. Of course, we are not absolutely certain that it will. We might be wrong, due to unforeseen circumstances. However, the evidence that supports our prediction is solid.

Similarly, the reason why in certain cases it does not seem correct to assert that things will go a certain way is that in those cases we do not know whether things will go that way; that is, it may easily be false that things will go that way. We are not in a position to tell whether exactly 3,245 pigeons will walk in Piazza San Marco. As far as we know, the number of pigeons that will walk in Piazza San Marco may easily be bigger or smaller.

In this respect, assertions about the future resemble assertions about the past. The cases in which it seems correct to assert that things went a certain way are cases in which we take it to be true that things went that way. For example, it seems correct to assert that dinosaurs disappeared long time ago. Conversely, the cases in which it does not seem correct to assert that things went a certain way are cases in which we do not know whether things went that way. For example, it does not seem correct to assert that Caesar was annoyed by a mosquito while crossing the Rubicon.

More generally, the ordinary use of language suggests that assertions about the future, just like assertions about the past, can be correct or incorrect. Therefore, this suggests that future-tense sentences, like past-tense sentences, can be true or false. For example, “The sun will rise tomorrow” seems true. Conversely, “The sun will not rise tomorrow” seems false. Note that “The sun will rise tomorrow” does not express a necessary truth, that is, it is not a sentence such as “2+2=4.” Although unlikely, it is possible that it is false. Similarly, “The sun will not rise tomorrow” does not express a necessary falsity, that is, it is not a sentence such as “2+2=5.”

The problem discussed above, and that this article addresses, concerns future contingents; that is, sentences about future events that can occur or not occur. According to a line of thought that goes back to Aristotle, these sentences cannot be true or false. Hence, the linguistic analogy just considered is misleading: Assertions about the future are not like assertions about the past.

b. The Sea Battle

In chapter 9 of De Interpretatione, Aristotle asks whether it makes sense to say that a sentence about a future event that can occur or not occur is true or false. His answer is that it does not make sense, for if the sentence were true or false, then the event would be necessary or impossible:

Let us take, for example, a sea battle. It is requisite on our hypothesis that it should neither take place nor fail to take place tomorrow. These and other strange consequences follow, provided we assume in the case of a pair of contradictory opposites having universals for subjects and being themselves universal or having an individual subject, that one must be true, the other false, that there can be no contingency and that all things that are or take place come about in the world by necessity. (Aristotle, De interpretatione 18b23 ff)

Aristotle’s reasoning seems to be the following. Consider the sentences (1) and (2) as uttered today:

(1) There will be a sea battle tomorrow.

(2) There will not be a sea battle tomorrow.

If (1) were true, and (2) were false, then it would be settled today that there will be a sea battle tomorrow, so the sea battle would be necessary. Similarly, if (2) were true, and (1) were false, then it would be settled today that there will not be a sea battle tomorrow, so the sea battle would be impossible. Since the sea battle is contingent, that is, it is neither necessary nor impossible, this shows that (1) and (2) are neither true nor false.

For Aristotle, the claim that (1) and (2) are neither true nor false is consistent with the plausible assumption that the disjunction formed by (1) and (2) is true:

(3) Either there will be a sea battle tomorrow or there will not.

Aristotle seems to think that (3) expresses a necessary truth, although the same does not hold for (1) and (2) taken separately:

That every thing is or is not is necessary, and also that it will be or it will not be; however, certainly not that, taken separately, one or the other is necessary. I say for example that it is necessary that either there will be a sea battle tomorrow or there will not be a sea battle tomorrow, but it is neither necessary that a sea battle will occur tomorrow nor that it will not occur. Rather, it is necessary that it will occur or not. (Aristotle, De Interpretatione, 19a25-30)

Another aspect of Aristotle’s point is that the claim that (1) and (2) are neither true nor false does not reduce to the observation that we do not know whether there will be a sea battle tomorrow. Of course, we do not know whether there will be a sea battle tomorrow. The absence of truth or falsity that Aristotle ascribes to (1) and (2), however, is independent of our epistemic condition. The problem of future contingents concerns truth rather than knowledge. Compare (1) with “There was a sea battle yesterday.” We can easily imagine a situation in which one does not know whether a sea battle occurred the day before. Despite this, independently of whether one knows it or not, it seems right to say that “There was a sea battle yesterday” is either true or false. Its truth or falsity depends on what happened the day before. Aristotle suggests that (1) differs in this respect, because there is nothing that can make it true or false.

c. Bivalence, Excluded Middle, Fatalism

The problem of future contingents stems from the combination of three ingredients. Two of them are fundamental logical principles, namely, bivalence and excluded middle. The third is a controversial metaphysical doctrine, namely, fatalism.

Bivalence is the principle according to which truth and falsity are reciprocally exclusive and jointly exhaustive values. Classical logic relies on bivalence, in that it assumes that every sentence is true or false. If the letter p is used as a schematic expression that stands for any sentence, this assumption can be stated as follows:

(B) Either “p” is true or “p” is false.

For example, “p” can be replaced with “Snow is white,” “Snow is green,” or any other sentence.

Here, “any other sentence” includes not only simple sentences, such as those just considered, but also complex sentences, such as “Snow is not white,” “If snow is green, then it is not white,” and “Either snow is white or it is green.” The last three sentences are respectively a negation, a conditional, and a disjunction, in that they are formed by means of the connectives “not,” “if/then,” and “or.” In classical logic, complex sentences formed in this way are treated as truth functions of their constituents, which means that their truth or falsity is determined by the truth and falsity of their constituents. More precisely, the negation of a sentence is true if and only if the sentence is false, a conditional is true if and only if it is not the case that its antecedent is true and its consequent is false, and a disjunction is true if and only if at least one of its disjuncts is true. Thus, bivalence is consistent with the assumption that some connectives—such as “not,” “if/then,” and “or”—are truth-functional, that is, that the complex sentences formed by means of these connectives are truth functions of their constituents.

Excluded middle is the principle according to which every disjunction formed by a sentence and its negation is true. For instance:

(E) Either p or not-p

Classical logic justifies (E) in that it assumes that negation and disjunction are defined in the way explained. From that definition, it turns out that, no matter whether it is the case that p, one of the disjuncts of (E) must be true.

Finally, fatalism is the doctrine according to which nothing is contingent, that is, everything is either necessary or impossible:

(F) Either it is necessary that p or it is impossible that p

From (F) we get that if p, then it is necessary that p, and if not-p, then it is impossible that p. Suppose that p. Then the second disjunct of (F) is false, and hence the first must be true. Suppose that not-p. Then the first disjunct of (F) is false, and hence the second must be true. Note that here “necessary” and “impossible” are understood as “necessary given our past and our present” and “impossible given our past and our present,” that is, without taking into account what could happen if our past and our present were different. The problem of future contingents concerns future possibilities. It does not concern past or present possibilities.

The thesis that nothing is contingent is sometimes called “necessitarianism,” and the term “fatalism” often expresses the view that no one has free will, understood as the ability to do otherwise than what one actually does. However, even when a distinction is drawn between necessitarianism and fatalism, it is usually taken for granted that there is a close connection between them: If we are unable to do otherwise than we actually do, it is because what we do is necessary. In any case, independently of what “fatalism” means, (F) is controversial because it is at odds with free will. If nothing is contingent, then it is hard to see how one can be free to choose one course of action rather than another.

d. Two Arguments

The reasoning that emerges from the first quote in section 1.b suggests that bivalence entails fatalism. Suppose that (1) is either true or false. Assuming that the truth of (1) makes the sea battle necessary, and that the falsity of (1) makes the sea battle impossible, it follows that either it is necessary or it is impossible that there will be a sea battle. The argument may be phrased in schematic form as follows:

[BF]

(B) Either “p” is true or “p” is false.

(A1) If “p” is true, then it is necessary that p.

(A2) If “p” is false, then it is impossible that p.

So, (F) Either it is necessary that p or it is impossible that p.

[BF] is valid, in that its conclusion follows from its premises. Suppose that (B), (A1), and (A2) are true. Then one of the disjuncts of (B) is true. This means that either the antecedent of (A1) or the antecedent of (A2) is true, hence that either the consequent of (A1) or the consequent of (A2) is true. So (F) must be true. If one accepts the premises of a valid argument, one is compelled to accept its conclusion. Therefore, one cannot accept (B), (A1), and (A2) without accepting (F). By contraposition, if one takes (F) to be false, one must think that there is something wrong in the premises of [BF]. Aristotle thinks that the mistake lies in (B), as he takes (A1) and (A2) to be true.

Since (B) and (E) are distinct logical principles, rejecting (B) does not amount to rejecting (E). Aristotle is clearly aware of this fact, as shown by the second quote in section 1.2. However, there is another fact that he does not take into account, namely, that if one grants two apparently innocuous assumptions about truth and falsity, one can get bivalence from excluded middle. The argument is the following:

[EB]

(E) Either p or not-p.

(A3) If p, then “p” is true.

(A4) If not-p, then “p” is false.

So, (B) Either “p” is true or “p” is false.

[EB] is valid, as is [BF]. Here, again, the first premise is a disjunction, the second and third premises are conditionals in which the two disjuncts occur as antecedents, and the conclusion is a disjunction formed by the two consequents. This means that if (E), (A3), and (A4) are true, then (B) must be true.

Now the problem of future contingents becomes evident. According to [BF], bivalence entails fatalism. According to [EB], excluded middle entails bivalence. Therefore, from the combination of [EB] and [BF] we get that excluded middle entails fatalism. Since fatalism is unacceptable—or so assume Aristotle and many others after him—there must be something wrong with at least one of the premises of [BF] and [EB]. Determining which is the problem. Questions arise as to whether bivalence and excluded middle are sound logical principles, whether bivalence really entails fatalism, and whether excluded middle really entails bivalence. To solve the problem of future contingents is to provide satisfactory answers to these questions.

2. Three Logical Options

a. Neither Bivalence nor Excluded Middle

Now we will consider three distinct theses about bivalence and excluded middle, which constitute the main logical options available to solve the problem of future contingents. These three theses share two basic assumptions: One is that fatalism is wrong, and the other is that [BF] and [EB] are valid. Thus, they agree that (E) and (A1)-(A4) are not all true. If (E) and (A1)-(A4) were all true, on the second assumption it would follow that (F) is true, contrary to the first assumption.

The first option—option 1—is to deny both bivalence and excluded middle. According to this option, bivalence does not hold. Since (A1) and (A2) are true, if (B) were true, then (F) would be true. Excluded middle does not hold either, for (A3) and (A4) are just as true as (A1) and (A2). So, if (E) were true, then (B) would be true as well. In other terms, [BF] and [EB] are alike in that their first premise is false.

In the debate over future contingents, the theory that best expresses option 1 is Lukasiewicz’s three valued logic (Lukasiewicz 1970). This theory, which intends to provide a coherent interpretation of Aristotle, shares with classical logic the tenet of truth-functionality; that is, it takes for granted that the value of a complex sentence is determined by the values of its constituents. However, it differs from classical logic in that it contemplates three values instead of two: truth, falsity, and indeterminacy.

Lukasiewicz rejects bivalence because he thinks that some sentences are indeterminate. A sentence is indeterminate when the way things are does not make it true and does not make it false. For example, (1) is indeterminate, because no fact or event today can make it true or false.

Lukasiewicz also rejects excluded middle. In his logic, the negation of an indeterminate sentence is itself indeterminate. For example, (2) is indeterminate, for its truth would amount to the falsity of (1), and its falsity would amount to the truth of (1). Moreover, a disjunction is indeterminate if both its disjuncts are indeterminate. So (3) is indeterminate. In general, every disjunction formed by an indeterminate sentence and its negation turns out indeterminate.

The rejection of bivalence is an essential feature of any three-valued logic, for what defines such a logic is just the hypothesis that there are three values instead of two. The rejection of excluded middle, instead, is not essential in this sense. Assuming that there are three values, and that some connectives are truth-functional, there is no unique way to define those connectives. In particular, negation and disjunction could be so defined as to validate excluded middle.

However, it seems that there are no independent reasons for changing the definitions of negation and disjunction proposed by Lukasiewicz. First, it would make little sense to stipulate that the negation of an indeterminate sentence is true rather than indeterminate. Since (1) and (2) are about the same event, it is hard to see how (2) can be true if (1) is indeterminate. Second, it would make little sense to stipulate that a disjunction formed by two indeterminate sentences is true rather than indeterminate, because in that case, “Either there will be a sea battle tomorrow or it will rain tomorrow” would be true, which seems unreasonable.

On the other hand, from the perspective of a three-valued logic it would be impermissible to claim that some negations of indeterminate sentences are indeterminate while others are true, or that some disjunctions formed by indeterminate sentences are indeterminate while others are true. This would amount to giving up truth-functionality, which is essential to any such logic. To assume that “not” and “or” are truth functional is to assume that the value of a negation or a disjunction—no matter whether truth, falsity, or indeterminacy—solely depends on the value of its constituents.

Thus, although Lukasiewicz’s logic is not the only three-valued logic that we can imagine, it is reasonable to think that no other three-valued logic can provide a better account of future contingents. Accordingly, we assume that three-valued logic invalidates both bivalence and excluded middle.

One merit of option 1 is that it accepts [EB]. This is plausible, given that [EB] is valid and that (A3) and (A4) express principles about truth and falsity that seem evident. According to [EB], if one accepts (E), one must also accept (B). So, by contraposition, if one rejects (B), one must also reject (E).

The rejection of excluded middle, however, constitutes a flaw of option 1, for it is hard to believe that a disjunction formed by a sentence and its negation, such as (3), is not true. Even though we do not know what will happen tomorrow, it seems certain that either there will be a sea battle tomorrow or there will not.

Another problem that affects option 1—the assertion problem—derives from the rejection of bivalence. As we have seen in section 1.a, the ordinary use of language suggests that some assertions about the future are correct, and hence that some future contingents are true. For example, “The sun will rise tomorrow” seems true. If all future contingents are indeterminate, however, this sentence cannot be true, so it is not clear why one should assert it. Those who adopt option 1 must explain how we can make apparently correct assertions by using future contingents.

b. Excluded Middle without Bivalence

The second option—option 2—is to deny bivalence but accept excluded middle. According to this option, bivalence entails fatalism, but excluded middle does not entail fatalism, because excluded middle does not entail bivalence. In other words, the argument that does not work is [EB], for one can accept (E) without accepting (B). This is the most plausible reading of Aristotle, advocated by Boethius, Peter Auriol, and many other scholars.

To justify option 2, one must explain why [EB] does not work. That is, one must explain why (A3) and (A4) are not true. Supervaluationism, a theory elaborated by Thomason (1984) on the basis of ideas expressed by Prior (1967) and Van Fraassen (1966), provides one coherent explanation. Supervaluationism rests on the assumption that future-tense sentences can be evaluated as true or false relative to possible futures. For example, in some possible futures there will be a sea battle tomorrow, while in others there will be peace. (1) is true in a future of the first kind, while it is false in one of the second kind. According to supervaluationism, to ask whether a future-tense sentence is true or false is to ask whether it is true or false in any possible future. This idea can be phrased in a precise way if we define a “history” as a whole possible course of events, that is, a course of events that includes a possible future, and we assume that, for any future contingent “p,” uttered at a moment m, there is a set of accessible histories such that in each of them “p” is either true or false at m. Truth in the non-relative sense—truth simpliciter—is defined in terms of truth relative to histories: “p” is true at m if and only if it is true at m in all the histories of the set. Similarly, “p” is false at m if and only if it is false at m in all the histories of the set. The name of the theory comes from this idea. If we call “valuation” each attribution of value to a sentence relative to a history, we can call “supervaluation” an attribution of value to the sentence that takes into account all the valuations.

Supervaluationism draws a principled distinction between bivalence and excluded middle. Consider (1). Since (1) is true today in some histories and false today in other histories, (1) is neither true nor false today. The same goes for (2). In general, future contingents are neither true nor false, because they are true in some histories and false in others. Therefore, bivalence does not hold. Now consider (3). In every history, either the first disjunct is true today, or the second disjunct is true today. Consequently, (3) is true today. In general, a disjunction formed by a sentence and its negation is always true. Therefore, excluded middle holds.

Note that this account of excluded middle involves an essential duality with respect to truth-functionality. There is a sense in which (3) is a truth function of its constituents, the sense in which, for any history h, (3) is true in h if and only if one of its disjuncts is true in h. There is also a sense in which (3) is not a truth function of its constituents, the sense in which (3) is true simpliciter even though neither of its disjuncts is true simpliciter. Truth-functionality holds at the level of truth relative to histories, but not at the level of truth simpliciter. This makes supervaluationism a partially non-classical theory.

Now let us go back to (A3) and (A4). Supervaluationism provides a motivation for rejecting (A3). Suppose that “p” is a future contingent that is true at m in h. Then the antecedent of (A3) is true at m in h. Its consequent, however, is not true at m in h, because in order to be true at m in h, “p” should be true at m in all histories. Therefore, (A3) is not true at m in h. It follows that (A3) is not true at m. A similar reasoning motivates the rejection of (A4). Suppose that “not-p” is a future contingent that is true at m in h. Then the antecedent of (A4) is true at m in h. Its consequent, however, is not true at m in h, because “p” is not false at m in all histories. So (A4) is not true at m in h. It follows that (A4) is not true at m.

Although this explanation is consistent with the supervaluationist definition of truth, it is not entirely satisfactory, or so one might argue. The rejection of (A3) and (A4) speaks against supervaluationism, for (A3) and (A4) are very plausible assumptions. It seems trivial that “Snow is white” is true if snow is white, and that “Snow is white” is false if snow is not white. Just because it seems trivial, it should turn out true.

Independently of (A3) and (A4), the supervaluationist definition of truth may cause some perplexity. Some might contend that this definition mistakenly identifies truth with necessity. To say that “p” is true is not the same thing as to say that it is necessary that p, or so it appears. Imagine that Bob and Rob are at the racecourse and that Bob bets on Frisco. Bob and Rob are indeterminists, so they believe that it is possible that Frisco will win and that it is possible that Frisco will not win. In the middle of the race, Rob says to Bob: “Don’t worry, Frisco will win,” to which Bob replies, “I really hope that’s true.” Presumably, what Bob hopes is not that his philosophical convictions are false; that is, he does not hope that Frisco’s victory is necessary. To hope that Frisco will win is not the same thing as to hope that it is necessary that Frisco will win. It is consistent to hope that Frisco will win and think that it is possible that Frisco will not win. It thus seems that the truth of the sentence uttered by Rob does not amount to its truth in all histories.

The intuitive difference between the claim that “p” is true and the claim that it is necessary that p becomes even clearer when we consider retrospective attributions of truth. Suppose that Frisco really wins and that at the end of the race Bob exults: “You were right! It was true!” What Bob wants to say is that the sentence uttered by Rob during the race was true. However, the supervaluationist definition of truth entails that that sentence was neither true nor false, as it was false in some histories. This seems wrong, because the truth that Bob retrospectively attributes to the sentence uttered by Rob does not rule out its possible falsity. It is consistent to think that what Rob said was true and that, in the moment in which he said it, it was possible that Frisco would not win. Again, it seems that the truth of the sentence uttered by Rob does not amount to its truth in all histories.

Supervaluationism is not the only theory in line with option 2. Another theory, advocated by Belnap and others (Belnap, Perloff, and Xu 2001), implies that there is no such thing as truth simpliciter. Future contingents are true or false only relative to histories, because it is only relative to histories that they express a determinate content. Suppose that (1) is uttered today. Since at the moment of the utterance different futures are possible, each of which includes a different tomorrow, the word “tomorrow” in (1) does not denote a determinate moment, which means that (1) does not express a determinate content. Therefore, it makes no sense to ask whether (1) is true or false today. The only meaningful question that can be asked is whether (1) is true or false relative to a given history. This theory shares with supervaluationism the assumption that future contingents can be evaluated as true or false relative to possible futures, but does not identify truth simpliciter with truth in all histories, because it rejects the very idea of truth simpliciter.

MacFarlane (2003, 2008) has proposed a third theory. Just like Belnap and others, MacFarlane claims that there is no such thing as truth simpliciter. In this case, the motivation provided is that a parameter of evaluation other than the history has to be taken into account. According to MacFarlane, the value of a future contingent uttered at a given moment can vary depending on the context of assessment, that is, on the moment in which it is evaluated. Suppose that (1) is uttered today and that tomorrow there is a sea battle. Today, at the moment of the utterance, (1) is neither true nor false. Tomorrow, however, in the middle of the sea battle, (1) is true. Consequently, the same sentence, as uttered at a given moment, can have different values in different contexts of assessment.

Both theories reject bivalence: Future contingents are not true or false, because they are not true or false in some absolute sense. Moreover, they both preserve excluded middle, because they make it valid in a relative sense. For example, (3) is always true today, in that it is true today in every history or in any context of assessment. These two theories thus have much in common with supervaluationism.

Leaving specific problems aside, both theories considered run into the assertion problem, as they reject bivalence. If one claims that “The sun will rise tomorrow” is neither true nor false, independently of the motivation adopted, one has to explain why it seems correct to assert this sentence.

To conclude, option 2 differs from option 1 in that it saves excluded middle, which is a merit. Its main flaws are essentially two. One is that it must provide a plausible definition of truth that—among other things—enables us to explain what is wrong with [EB]. The other is that it must address the assertion problem, which it shares with option 1.

c. Both Bivalence and Excluded Middle

The third option—option 3—is to accept both bivalence and excluded middle. According to this option, excluded middle entails bivalence, but bivalence does not entail fatalism. In other terms, the argument that does not work is [BF], for one can accept (B) without accepting (F).

To justify option 3, one must explain why [BF] does not work, that is, it must be explained why (A1) and (A2) are not true. One way to do so is to endorse Ockham’s idea that one of the possible futures is the actual future, that is, the way things will actually go. In his Tractatus de praedestinatione et praescientia Dei respectu futurorum contingentibus, which aims to explain how divine foreknowledge is compatible with the contingency of events, Ockham draws a distinction between truth and determinate truth. The former is understood as truth in the actual future, the latter is understood as truth in all possible futures. According to Ockham, future contingents are true or false, even though they are not determinately true or determinately false (1978).

The distinction between truth and determinate truth—which has been defended by Von Wright (1984), Lewis (1986) and Horwich (1987), among others—can be illustrated by means of the two examples considered in section 2.b. Suppose, as before, that Rob says to Bob, “Don’t worry, Frisco will win!” and that Bob replies, “I really hope that’s true.” As we have seen, it seems that Bob’s hope is not that Frisco’s victory is necessary. One obvious candidate for what he does hope for is the following: What Bob hopes is that Frisco will actually win, namely, that the possible future that will become reality is a future in which Frisco wins. Now, suppose that Frisco really wins and that Bob says to Rob: “You were right! It was true!” As we have seen, it seems correct to say that the sentence uttered by Rob was true, even though it was possible that Frisco would not win. If the truth of that sentence does not amount to its truth in all possible futures, it is unclear what it amounts to. Again, one obvious answer is that it amounts to the fact that Frisco actually won. Thus, a sentence can be true without being determinately true, if it is true in the actual future but false in some other future.

The theory that we will call Ochkamism is inspired by Ockham in that it defines truth in terms of the actual future. Ockhamism, just like the theories considered in section 2.b, adopts a relative notion of truth: A future contingent “p,” uttered at a moment m, can be evaluated as true or false in a set of accessible histories. Truth in the non-relative sense—truth simpliciter—is defined in terms of this notion: “p” is true at m if and only if “p” is true at m in the actual history. Similarly, “p” is false at m if and only if “p” is false at m in the actual history (Øhrstrøm 2009; Rosenkranz 2012; Iacona 2013, 2014; Wawer 2014; Malpass and Wawer 2018).

If truth is defined in terms of the actual history, then truth does not entail determinate truth. This is why Ockhamism rejects (A1) and (A2). Suppose that “p” is true at m in the actual history. In this case, the antecedent of (A1) is true at m, while its consequent is false at m. Similarly, suppose that “p” is false at m in the actual history. In this case, the antecedent of (A2) is true at m, while its consequent is false at m.

This prompts the question of whether it makes sense to say that one of the possible futures is the actual future. The very idea of a unique actual future may easily raise doubts and misgivings. If one among the many possible futures is the actual future, it is unclear how the other futures can be equally possible, given that they will not become real. In other words, it seems impossible that what will happen is not predetermined. In order to adequately justify the distinction between truth and determinate truth, some convincing responses to these questions must be provided.

In sum, option 3 rescues bivalence and excluded middle, in accordance with classical logic. Moreover, it does not run into the assertion problem, because it implies that some future contingents are true, so it can explain the apparent correctness of some assertions about the future. The most problematic aspect of this option is the very idea of the actual future.

d. Further Considerations

The three logical options considered so far define the main positions within the debate on future contingents. Since these options do not exhaust the logical space of possibilities, this section dwells briefly on the only combination this article has not considered, namely, bivalence without excluded middle.

One way to give substance to this option, which comes from Pierce as interpreted by Prior, is the following: Future contingents are all false, because they describe future events as inevitable. For example, (1) and (2) are both false, because (1) says that there will necessarily be a sea battle tomorrow, while (2) says that there cannot be a sea battle tomorrow. Therefore, excluded middle does not hold: (3) is false, for both its disjuncts are false. Yet bivalence holds, because every sentence, including future contingents, is either true or false (Øhrstrøm and Hasle 1995; Prior 1967; Todd 2016).

The same problems that affect option 1 affect this position. First, the rejection of excluded middle is difficult to accept. (3) seems true, not false. Second, the assertion problem is still there. If all future contingents are false, then “The sun will rise tomorrow” cannot be true, in spite of the fact that it seems correct to assert it.

Independently of these two problems, the idea that all future contingents are false gives rise to further troubles. Consider (1) and (2). On the assumption that (2) is the negation of (1), as its syntactic structure suggests, it is unreasonable to think that (1) and (2) are both false. So, the most plausible way to claim that (1) and (2) are both false is to say that (2)—contrary to what its syntactic structure suggests—is not the negation of (1). The negation of (1) would rather be “It is not the case that there will be a sea battle tomorrow.” On the hypothesis that (2) and “It is not the case that there will be a sea battle tomorrow” express different contents, it is consistent to say that the former is false while the latter is true. Note, however, that this way, “Either there will be a sea battle tomorrow or it is not the case that there will be a sea battle tomorrow” turns out true. Thus, there is a clear sense in which excluded middle holds: If “It is not the case that there will be a sea battle tomorrow” is the negation of (1), the sentence that instantiates (E) is “Either there will be a sea battle tomorrow or it is not the case that there will be a sea battle tomorrow,” not (3). Moreover, we still need an explanation of why (2) and “It is not the case that there will be a sea battle tomorrow” express different contents, given that they seem to say exactly the same thing.

These troubles explain the scarce popularity of the option just considered. The debate on future contingents almost never sees the acceptance of bivalence combined with the rejection of excluded middle, because most thinkers take it for granted that bivalence is at least as controversial as excluded middle.

3. Three Metaphysical Views

a. Past, Present, and Future Entities

So far, we have considered three logical options that differ with respect to bivalence and excluded middle. Now we will address the key metaphysical issue that underlies the problem of future contingents: what there is in front of us.

Let us first introduce four basic ontological conceptions of time, that is, four conceptions of the existence of past, present, and future entities. Past entities and future entities resemble present entities in some respects but not in others. On the one hand, there is a sense in which Caesar is like us and unlike the Abominable Snowman: Ceasar was a real person, while the Abominable Snowman has never existed. The same goes for future children, who will be real persons just like us. On the other hand, there is a sense in which Caesar is not like us: We are here, while he is no longer here. Similarly, future children are not here yet. The four conceptions considered in this article weigh these similarities and differences in different ways.

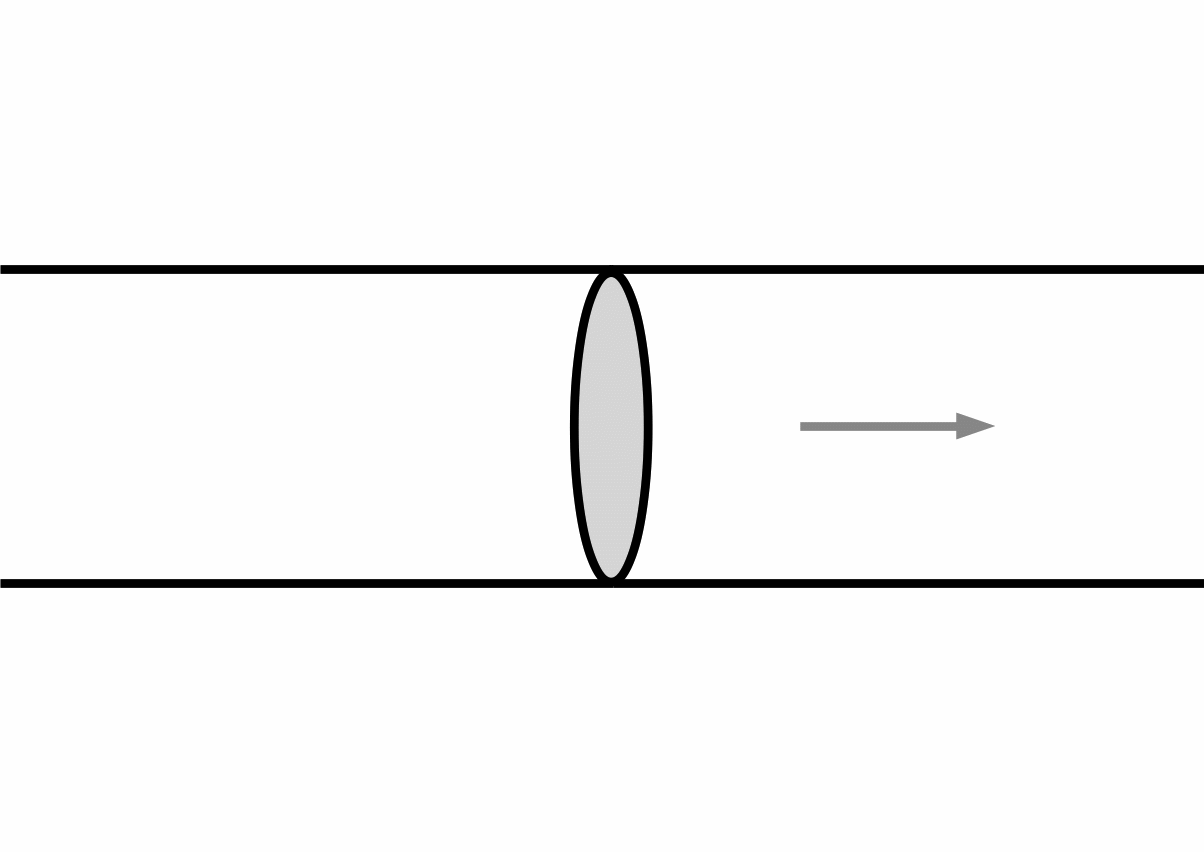
Presentism is the conception according to which only present entities exist. We exist, but Ceasar and future children do not exist. Existing and being present are the same thing. Imagine an incredibly big and incredibly thin slice of salami. The slice is the present, and we are in it. Behind us there is nothing, because the past does not exist, and ahead of us there is nothing, because the future does not exist. This conception—which is defended by Prior (1970), Bigelow (1996), and Bourne (2006), among others—is represented in figure 1.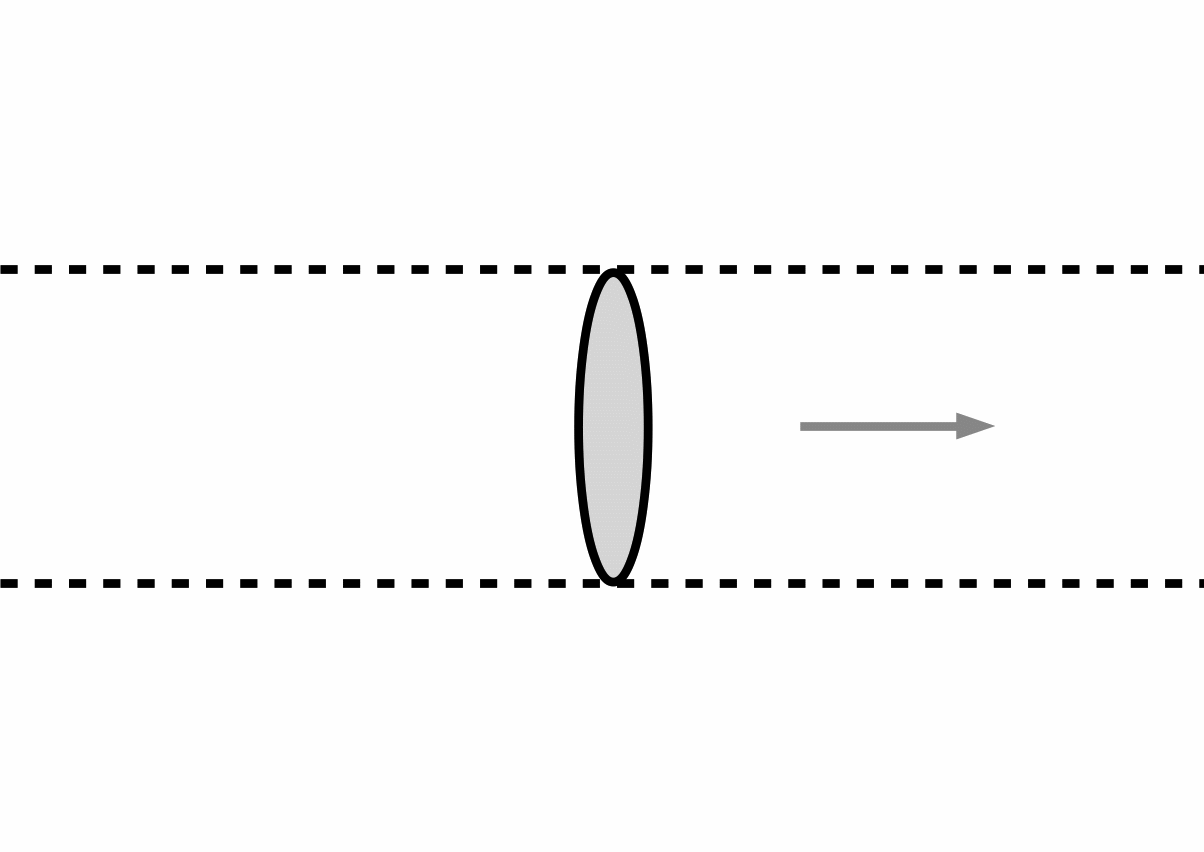

Figure 1: Presentism

The growing block theory, alternatively, is the conception according to which past and present entities exist, but future entities do not exist. Ceasar exists, we exist, but future children do not exist. This conception—defended by Broad (1923), Tooley (1997), and Correia and Rosenkranz (2018), among others—describes reality as a totality that constantly increases as time passes. In figure 2, the slice of salami that represents the present is attached to the portion of salami that precedes it, the past.

Figure 2: Growing block

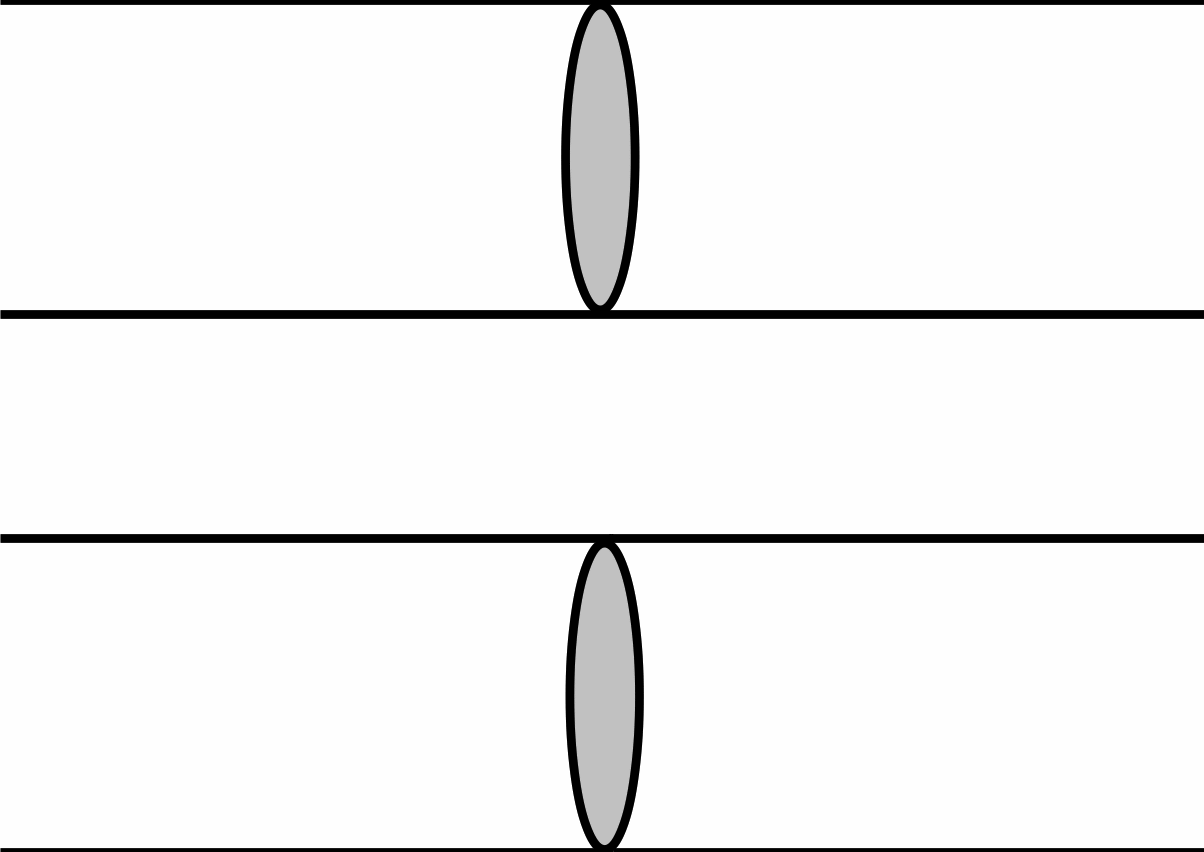
A third conception that is purportedly opposite to the growing block theory is the shrinking block theory. According to this theory, which is not widely accepted (though see, for example, Casati and Torrengo 2011), present and future entities exist, but past entities do not exist. We exist, future children exist, but Ceasar does not exist. Reality is what is left, so to say, and the future is constantly eroded as time passes. In figure 3, the slice of salami that represents the present is attached to the portion of salami that follows it, the future.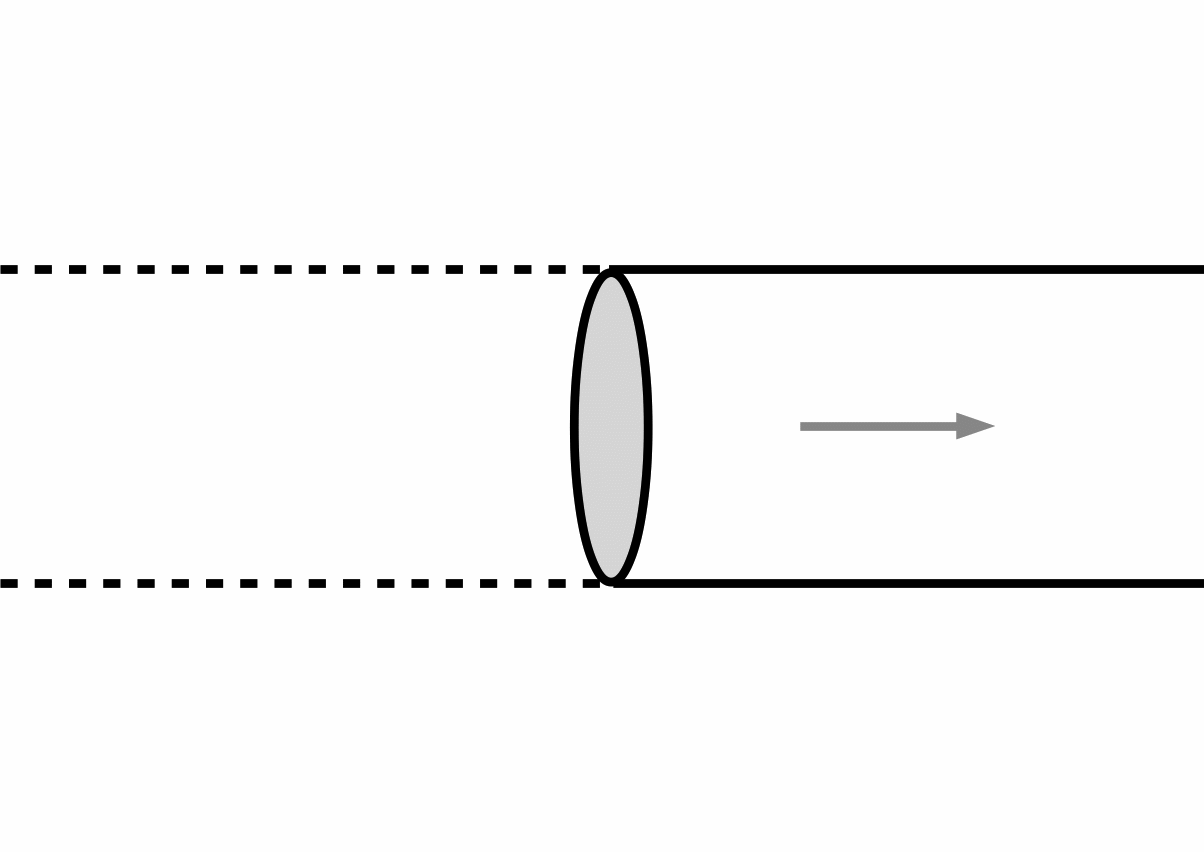

Figure 3: Shrinking block

Finally, eternalism is the view according to which past, present, and future entities exist. We exist, and the same goes for Ceasar and future children. This conception is defended by Williams (1951), Taylor (1955), Smart (1963), Putnam (1967), Mellor (1998), and Sider (2001), among others. In figure 4, the slice of salami that represents the present is part of a whole salami, a history, which may be conceived of as a sequence of moments.

Figure 4: Eternalism

While the first three conceptions are essentially dynamic, in that they imply that the passage of time is metaphysically real, eternalism may be understood either dynamically, assuming that the present really moves along the line of time, or statically, assuming that the experience of the passage of time is merely illusory. On both interpretations, the idea that underlies eternalism is that temporal relations are somehow similar to spatial relations. For example, Turin, Milan and Venice are located on three points ordered along the west-east axis. Although each of these three cities offers a distinct perspective on the other two, the spatial relations among them—the order in which they are located along the west-east axis—do not vary with the point of observation. According to eternalism, the same goes for temporal relations. Being present is like being in Milan. There is no ontological difference between Caesar, us, and future children, just as there is no ontological difference between Turin, Milan, and Venice (see the time).

The classification just presented will help with understanding the three metaphysical views considered in the next three sections. As these sections show, these three views can be associated with options 1-3, although there is no necessary connection between them. Each view provides a distinct answer to the question of what is there ahead of us.

b. No Future

The first view—the no-future view—says that there is absolutely nothing ahead of us: The future does not exist. Certainly, many things will happen, and it makes perfect sense to talk about such things. However, what will happen will exist only when it will happen; it does not exist now. When it will happen, it will no longer be future.

Presentism and the growing block theory entail the no-future view. Although these two conceptions differ with respect to the question of whether the past exists, they agree on the non-existence of the future. By contrast, the shrinking block theory and eternalism contradict the no-future view. Although these two conceptions differ with respect to the question of whether the past exists, they agree on the existence of the future. Therefore, the no-future view can be maintained either in a presentist perspective or in a growing-block perspective.

Of the three logical options considered in section 2, the one that best suits the no-future view is option 1. If the future does not exist, there is nothing that can make future-tense sentences true or false. For example, there is nothing that can make (1) and (2) true or false. It is thus sensible to claim that future-tense sentences violate bivalence. This is probably what Lukasiewicz had in mind, although he did not explicitly address the distinction between presentism and growing block theory.

Perhaps it is also sensible to claim that future-tense sentences violate excluded middle. If nothing can make true (1) or (2), the same goes for (3). The “perhaps” is due to the fact that the inference from the absence of truth of (1) and (2) to the absence of truth of (3) requires a further constraint that plays a crucial role in three-valued logic, namely, truth-functionality. Assuming that a disjunction is true only if one of its disjuncts is true, from the absence of truth of (1) and (2) we can infer the absence of truth of (3). Without that assumption, instead, the inference is not legitimate. As we have seen in section 2.2, supervaluationism differs from three-valued logic precisely in that it gives up truth-functionality to save excluded middle.

The no-future view—especially in the growing block version—provides a metaphysical substratum for the idea that future-tense sentences are sui generis from the logical point of view. The difference at the logical level can be explained by a difference at the metaphysical level: The past and the present exist, whereas the future does not exist. This is not to say that, strictly speaking, the no-future view entails that idea. For example, Correia and Rosenkranz (2018) argue that the growing block theory is consistent with bivalence.

c. Many Futures

The second and the third view differ from the first in that they entail the existence of future entities. Although this makes them compatible both with the shrinking block theory and with eternalism, they are usually framed in an eternalist perspective. In such a perspective, the contingency of a future event cannot be conceived of in terms of absence, as in the no-future view, because an event cannot be future without existing. Rather, it will be conceived of in terms of presence in some but not in all possible futures. This is why the second and the third view contemplate a plurality of histories. A history is a possible world, that is, a totality of past, present, and future entities that is completely defined in its spatial and temporal properties.

The second view—the many-futures view—says that there are many futures ahead of us, that is, many possible continuations of the present. These continuations are like branches that depart from the same trunk, and they are metaphysically on a par, that is, they all exist and they are all actual (or none of them is). Figure 5 illustrates the many-futures view by recalling the salami analogy. The slice is the present, as in the previous figures, but there are two portions of salami on the right, that is, two possible continuations of the present. Each of these two portions, together with the left portion, forms a whole salami. Therefore, the slice belongs to two distinct salami.

Figure 5: Branching

The idea illustrated in figure 5 can be represented in a more abstract way by using simple lines. In figure 6, h₁and h₂are histories, while m₀, m₁and m₂are moments. m₀belongs both to h₁and to h₂. Instead, m₁belongs only to h₁, and m₂belongs only to h₂. While m₀precedes both m₁and m₂, m₁and m₂are unrelated, in that neither of them precedes the other. Diagrams of this kind, introduced by Kripke and Prior, are often employed in temporal logic to represent the set of future possibilities (Prior 1967).

Figure 6: One past, one present, two futures

The case of the sea battle can be described in terms of this figure. Suppose that m₀is today, that is, the moment at which (1) and (2) are uttered. h₁and h₂are histories that lead to different tomorrows: m₁is a peaceful tomorrow, while m₂is a tomorrow in which there is a sea battle. h₁and h₂have a part in common, that is, our past until today. The two portions of h₁and h₂that follow m₀are distinct possible futures. The contingency of the sea battle consists precisely in the existence of these futures.

Note that figure 6 shows two distinct tomorrows instead of one. Each of these two tomorrows belongs only to one history. However, this does not mean that it makes no sense to describe m₁and m₂as simultaneous. On the contrary, assuming that there is an absolute temporal axis, that is, that time can be measured from a point of view that is external to the histories, we can say that m₁and m₂are located at the same point along that axis. If we call instant an absolute temporal unit, definable as a set of equivalent moments, we can say that two moments that belong to different histories are in the same instant. In figure 7, i₀is the present instant, that is, the instant that includes m₀, and i₁is the instant that includes m₁and m₂.

Figure 7: The sea battle

The many-futures view is clearly in line with option 2. In the framework just sketched, future contingents can be evaluated as true or false at moments relative to histories. For example, (1) is true at m₀in h₂but false at m₀in h₁. Similarly, (2) is true at m₀in h₁but false at m₀in h₂. According to the supervaluationist definition of truth, this entails that (1) and (2) are neither true nor false at m₀, so that bivalence does not hold. Instead, excluded middle holds. (3) is true at m₀, for it is true at m₀both in h₁, given that (2) is true at m₀in h₁, and in h₂, given that

(1) is true at m₀in h₂. The two further theories considered in section 2.b fit the many-futures view equally well, in that they employ the same notion of truth relative to histories.

d. One Future

The third view—the one-future view—says that there is one future ahead of us, our future. This view has two versions. According to one of them—the thin red line—many possible futures depart from our present, but these futures are not metaphysically on a par because only one of them is actual. According to the other—divergence—we have a single future because we belong to a single history, the actual history, although there are other histories that are exactly like our history up to the present but have a different future. The key difference between the two versions concerns the possibility of overlap. To endorse the thin red line is to think that two histories can overlap, that is, that they can have some part in common. To endorse divergence, instead, is to conceive histories as entirely disconnected totalities. Here we will focus on divergence, although what will be said applies, mutatis mutandis, to the thin red line.

Figure 8 illustrates divergence. Imagine that we are in the salami below, and that the left portion of the salami above—the portion that precedes the slice—is identical to the left portion of our salami, but that the right portion of the salami above—the portion that follows the slice—differs from the right portion of our salami. In this case the two salami are divergent histories.

Note that figure 8 shows two presents, each of which belongs to a single history. This is not to say that it makes no sense to describe such moments as simultaneous. As in the many-futures view, simultaneity can be defined in terms of instants. Figure 9 represents the two histories considered above as horizontal lines, h₁and h₂, and represents the instant that the two presents have in common as a vertical line that intersects h₁and h₂. Our present, m₀, is in h₁and differs from m₁, which is in h₂. However, m₀and m₁are simultaneous in the sense that they belong to the same instant i₀.

Figure 8: Divergence

Figure 9: Two pasts, two presents, two futures.

The question is who the individuals in the other history, who are exactly like us up to now, are. Lewis, who defends divergence, calls such individuals counterparts. If we are in h₁, then in h₂there are other individuals who are our counterparts. Just as we have a future, the right portion of h₁, our counterparts have their own future, the right portion of h₂(Lewis 1986).

Now let us go back to the sea battle. Figure 10 represents two histories h₁and h₂that are exactly alike up to i₀but then differ. m₀and m₁are two distinct but qualitatively identical todays, each of which has its own tomorrow: m₂is a peaceful tomorrow, while m₃is a tomorrow in which there is a sea battle. Therefore, (1) is true at m₁, while it is false at m₀. Since m₁and m₀belong respectively to h₂and h₁, this is to say that (1) is true in h₂, while it is false in h₁. Whether (1) is true or false simpliciter depends on which of the two histories is the actual history. If we are in m₀we will have peace, whereas if we are in m₁we will find ourselves in the middle of a sea battle.

Figure 10: The sea battle

It is important to note that being in a given history does not mean being in a position to discern that history from other histories. Suppose that we are in h₁. Since m₀is qualitatively identical to m₁, and the same goes for any moment that precedes m₀, for us h₁is indistinguishable from h₂. So at i₀we are not in a position to know whether we are in h₁or in h₂. Consequently, we are not in a position to know whether our future includes m₂or m₃. In a way, we do not know what will happen tomorrow because we do not know where we are.

The one-future view suits option 3. The framework just sketched preserves bivalence. Suppose, as before, that (1) is true at m₁and false at m₀. Then, no matter which of the two histories is the actual history, (1) is either true or false. This is not to say that (1) is determinately true or determinately false. Assuming that determinate truth at a moment amounts to truth at all moments in the same instant, and that determinate falsity at a moment amounts to falsity at all moments in the same instant, (1) is neither determinately true at m₁nor determinately false at m₀. Excluded middle is preserved as well. (3) is true both at m₀and at m₁. Therefore, it is determinately true.

4. The Open Future

a. Alternative Possibilities

Most discussions on future contingents take for granted that fatalism is wrong. Despite this, it is not obvious what the right view is. The thought that underlies the rejection of fatalism is often expressed by saying that the future is open. The contemporary literature on future contingents, widely employs the metaphor of openness to characterize the view that the future is unsettled. Yet it is possible to understand openness in more than one way. This last section provides some clarifications about the claim that the future is open.

A simple and straightforward way to interpret the claim that the future is open is to define openness in terms of the existence of alternative possibilities: To say that the future is open is to say that, for some “p,” it is possible that p and it is possible that not-p. This interpretation is simple and straightforward because it equates the claim that the future is open with the pure negation of fatalism. As it turns out from section 1.c, fatalism is the claim that, for every “p,” either it is necessary that p or it is impossible that p. Consequently, its negation is the claim that, for some “p,” it is neither necessary nor impossible that p, that is, it is possible that p and it is possible that not-p.

If the openness of the future is understood in terms of the existence of alternative possibilities, then it is consistent with the three metaphysical views outlined in section 3. If one endorses the no-future view, one can say that, although there is presently nothing ahead of us, it is possible that what will exist is such that p and it is possible that what will exist is such that not-p. If one endorses the many-futures view, one can say that there are possible futures in which p and possible futures in which not-p. The same goes for the one-future view, even though in the case of divergence the possible futures have distinct pasts and distinct presents.

b. Indetermination

Another way to interpret the claim that the future is open is to define openness in terms of indetermination, understood as absence of determination: To say that the future is open is to say that nothing determines the future. This can mean two things: either that the future is not determined by some divine entity, or that the future is not determined by the laws of nature. Here we focus on the second reading, which became widespread by the early 21^st century, although these considerations apply to the first as well.

The idea that every event is determined by the laws of nature goes back to antiquity and has been widely discussed in modern and contemporary philosophy. According to this idea, every event follows as an effect from some cause in accordance with the laws of nature. Determination may be defined as a relation between states, understood as global conditions in which the universe can be at an instant. Given a state S that obtains at i₀and given a state S⁰that obtains at i₁, S determines S⁰if and only if the obtaining of S at i₀, together with the laws of nature, entails that S⁰obtains at i₁. Determinism is the view that, for every instant, the state that obtains at that instant is determined by the states that obtained at previous instants (Hoefer, 2003).

None of the three metaphysical views outlined in section 3 entails determinism. Suppose that i₀is the present instant and that S is the state of the universe at i₀. According to the no-future view, given an instant i₁later than i₀, nothing exists in i₁, even though when we will be in i₁, another state S⁰will obtain. The no-future view says nothing about the relation between S and S⁰, so it is consistent with the hypothesis that S does not determine S⁰. Now consider the many-futures view. Suppose, as in figure 7, that m₀is the present moment and that m₁and m₂are future moments that belong to i₁. If S is the state that obtains at m₀, while S⁰and S⁰⁰are the states that obtain respectively at m₁and m₂, then S determines neither S⁰or S⁰⁰, for it is compatible both with S⁰and with S⁰⁰. Finally, consider the one-future view. Suppose, as in figure 10, that m₀and m₁are in i₀, and that m₂and m₃are in i₁. If S is the state that obtains at m₀and m₁—in that h₁and h₂are identical up to i₀while S⁰and S⁰⁰are the states that obtain respectively at m₂and m₃—then S determines neither S⁰or S⁰⁰, for it is compatible both with S⁰and with S⁰⁰.

It is important to note that indetermination is not the same thing as indeterminateness, understood as absence of determinateness. If determinateness is the property that a possible future has when it is completely defined in its spatial and temporal properties, then indetermination does not entail indeterminateness. It is consistent to claim, as in the case of branching or divergence, that indetermination holds because there are many possible futures, each of which is completely defined in its spatial and temporal properties. Indetermination and indeterminateness are independent properties.

c. Causal Power

A third way to interpret the claim that the future is open is to define openness in terms of causal power: To say that the future is open is to say that we can affect the future, in that our present actions have future effects. For example, if tonight we set the alarm on our phone to 7 a.m., the sound that the phone will emit tomorrow at 7 a.m. is an effect of the movements that we perform tonight.

The idea that our present actions have future effects is obviously consistent with the three metaphysical views outlined in section 3. In each of the three cases, it makes perfect sense to say that an event which occurs at a given time causes another event that occurs at a later time.

Note that the past does not depend on us in the same sense, because our present actions do not have past effects. This asymmetry can be described in terms of counterfactual dependence, as Lewis has suggested. The future counterfactually depends on the present, because it would be different if the present were different. Suppose that tonight we set the alarm on our phone to 7 a.m. It is correct to say that, if the alarm were not set, the phone would not emit any sound tomorrow at 7 a.m. Instead, the past does not counterfactually depend on the present, because it would not be different if the present were different. If the alarm were not set, what happened yesterday would remain exactly the same (Lewis 1979).

The claim that we can affect the future must not be confused with the claim that we can change the future, that is, that we can replace the future with another future. It is one thing is to say that a future event, such as the sound that the phone will emit tomorrow at 7 am, is caused by a present event; it is quite another thing is to say that a future event can be replaced by a different future event. The claim that we can change the future is hardly intelligible, or so it appears to most philosophers (an exception is Todd 2016). In any case, this claim seems incompatible with the three metaphysical views outlined in section 3. If the no-future view is true, then the future does not exist, so nothing can be changed. If the many-futures view is true, then there are many possible futures, so it makes no sense to say that we can change “the” future. And in any case, each of the possible futures is essentially identical to itself. Finally, if the one-future view is true, then there is a unique future, which cannot be changed.

d. Other Definitions

As it turns out from sections 4.a-4.c, there are three plausible interpretations of the claim that the future is open: The first is that, for some “p,” it is possible that p and it is possible that not-p; the second is that the future is not determined; and the third is that we can affect the future. Each of these interpretations is consistent with the three metaphysical views outlined in section 3: No matter whether one endorses the no-future view, the many-futures view, or the one-future view, one can coherently claim that the future is open. Since options 1-3 accord, respectively, with the no-future view, the many-futures view, and the one-future view, this suggests that the claim that the future is open, on the three interpretations considered, is compatible with any solution to the problem of future contingents.

Of course, the three interpretations considered are not the only admissible interpretations. Other interpretations are possible. Nothing prevents us from defining openness in terms of some specific logical option or metaphysical view. The question then arises of whether the future is really open in the sense defined. Merely stipulating that openness amounts to this or that condition does not provide any reason to think that the stipulation captures some pre-theoretical intuition.

Some philosophers have suggested that the openness of the future amounts to the failure of bivalence for future-tense sentences (as in Markosian 1995). On this interpretation, the claim that the future is open yields substantive consequences, for it licenses options 1 and 2 while it rules out option 3. However, as some have observed (Barnes and Cameron 2009; Besson and Hattiangadi 2014), it is controversial whether the future is open in this sense. Aristotle needed an argument to show that bivalence does not hold for future contingents.

Other philosophers have suggested that the openness of the future amounts to the many-futures view: To say that the future is open is to say that there are multiple branching futures which are metaphysically on a par (as in MacFarlane 2003). On this interpretation, again, the claim that the future is open yields substantive consequences, for it rules out both the no-future view and the one-future view. However, it is controversial whether the future is open in this sense.

The controversy emerges clearly in the dialectic between branching and divergence. According to the advocates of the many-futures view, divergence does not preserve openness. Suppose that Betty wonders whether she can become an internationally acclaimed photographer. As far as divergence is concerned, the answer is affirmative if Betty will become a door-to-door cosmetics seller, but there is a history in which another individual very similar to Betty—call her Betty*—will become an internationally acclaimed photographer. The fact, however, is that what Betty wonders—what concerns her—is whether she, Betty, can become an internationally acclaimed photographer, not whether another person has that opportunity. It does not seem that Betty’s future be open if it only includes the sale of cosmetics. The openness of the future seems to imply that the alternative possibilities not only exist, but that they exist for the same individuals.

To this objection it might be replied that divergence does not deny that one and the same individual has alternative possibilities. Let us assume that “Betty can become an internationally acclaimed photographer” is true. Insofar as divergence explains the truth of this sentence in terms of the existence of a history in which Betty* becomes an internationally acclaimed photographer, the individual to whom it is correct to attribute the modal property of possibly becoming an internationally acclaimed photographer is Betty, not Betty*. Certainly, this explanation cannot be understood as a description of what Betty has in mind when she wonders whether she can become an internationally acclaimed photographer. However, the same holds for any other explanation of the same fact. Just as Betty does not think about Betty*, she does not think that she inhabits two histories that share a common segment and branch towards the future.

It is difficult to judge who is right. The objection against divergence stems from a line of thought that goes back to Kripke and that is antithetical to the theory of counterparts defended by Lewis. According to this line of thought, the truth or falsity of a sentence that attributes a modal property to an individual depends on what happens to the same individual in possible worlds other than the actual world. For example, Kripke claims that the sentence, “It might have been the case that Aristotle was not a philosopher,” is true because there are possible worlds in which Aristotle, the same Aristotle, was not a philosopher. The question of which of these two positions is preferable concerns possible worlds in general, and cannot be settled simply by appealing to intuitions.

5. References and Further Reading

Barnes, E. and Cameron, R. 2009. The Open Future: Bivalence, Determinism and Ontology. Philosophical Studies, 146:291–309.
Besson, C. and Hattiangadi, A. 2014. The Open Future, Bivalence and Assertion. Philosophical Studies, 162:251–271.
Bigelow, J. 1996. Presentism and Properties. Philosophical Perspectives, 10:35–52.
Bourne, C. 2006. A Future for Presentism. Oxford: Oxford University Press.
Broad, C. D. 1923. Scientific Thought. London: Routledge.
Casati, R. and Torrengo, G. 2011. The Not So Incredible Shrinking Future. Analysis, 71:240–244.
Correia, F. and Rosenkranz, S. 2018. Nothing To Come: A Defence of the Growing Block Theory of Time. Cham, Switzerland: Springer.
Dowden, B. 2018. Time. Internet Encyclopedia of Philosophy. https://www.iep.utm.edu/time/.
Hoefer, C. 2003. Causal Determinism. Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/determinism-causal/
Horwich, P. 1987. Asymmetries in Time. Cambridge (MA): MIT Press.
Iacona, A. 2013. Timeless Truth. In Around the Tree: Semantic and Metaphysical Issues Concerning Branching and the Open Future, edited by F. Correia and A. Iacona, 29–45. Cham, Switzerland: Springer.
Iacona, A. 2014. Ockhamism without Thin Red Lines. Synthese, 191:2633–2652.
Lewis, D. 1979. Counterfactual Dependence and Time’s Arrow. Noûs, 13:455–476.
Lewis, D. 1986. On the Plurality of Worlds. Oxford: Blackwell.
Lukasiewicz, J. 1970. On Three-Valued Logic. In Selected Works, edited by L. Borkowski, 87–88. Amsterdam: North-Holland.
MacFarlane, J. 2003. Future Contingents and Relative Truth. Philosophical Quarterly, 53:321–336.
MacFarlane, J. 2008. Relative Truth. In Truth in the Garden of Forking Paths, edited by M. Garcia-Carpintero and M. Kölbel, 81–102. Oxford: Oxford University Press.
Malpass, A. and Wawer, J. 2018. Back to the Actual Future. Synthese.
Markosian, N. 1995. The open past. Philosophical Studies, 79:95–105.
Mellor, H. 1998. Real Time II. London: Routledge.
Ockham, W. 1978. Tractatus de praedestinatione et de praecientia dei respectu futurorum contingentibus. In Opera philosophica et theologica, volume II. St. Bonaventure, New York: The Franciscan Institute.
Øhrstrøm. P. 2009. In Defence of the Thin Red Line: A Case for Ockhamism. Humana Mente, 8:17–32.
Øhrstrøm, P. and Hasle, P. F. V. 1995. Temporal Logic. From Ancient Ideas to Artificial Intelligence. Dordrecht: Kluwer.
Perloff, M., Belnap, N., and Xu, M. 2001. Facing the Future. Oxford: Oxford University Press.
Prior, A. N. 1967. Past, Present and Future. Oxford: Clarendon Press.
Prior, A. N. 1970. The Notion of the Present. Studium Generale, 23:245–248.
Putnam, H. 1967. Time and Physical Geometry. Journal of Philosophy, 64:240–247.
Rosenkranz, S. 2012. In Defence of Ockhamism. Philosophia, 40:617–31.
Sider, T. 2001. Four Dimensionalism. Oxford: Oxford University Press.
Smart, J. J. C. 1963. Philosophy and Scientific Realism. Humanities Press, 1963.
Taylor, R. 1955. Spatial and Temporal Analogies and the Concept of Identity. Journal of Philosophy, 52:599–612.
Thomason, R. H. 1984. Combinations of Tense and Modality. In Handbook of Philosophical Logic, volume 2, edited by D. Gabbay and G. Guenthner, 135–165. Dordrecht: Reidel.
Todd, P. 2016. On Behalf of a Mutable Future. Synthese, 193:2077–2095.
Tooley, M. 1997. Time, Tense, and Causation. Oxford: Oxford University Press.
van Fraassen, B. 1966. Singular Terms, Truth-Value Gaps, and Free Logic. Journal of Philosophy, 63:481–495.
von Wright, G. H. 1984. Determinism and Future Truth. In Truth, Knowledge, and Modality, 1–13. Oxford: Blackwell.
Wawer, J. 2014. The Truth about the Future. Erkenntnis, 79:365–401.
Williams, D. C. 1951. The Myth of the Passage. Journal of Philosophy, 48:457–472.

Author Information

Andrea Iacona
Email: andrea.iacona@unito.it
University of Turin
Italy

Internet Encyclopedia of Philosophy