Simplex

In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. Specifically, a k-simplex is a k-dimensional polytope which is the convex hull of its k + 1 vertices. More formally, suppose the k + 1 points 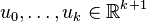are affinely independent, which means are linearly independent. Then, the simplex determined by them is the set of points

For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron, and a 4-simplex is a 5-cell. A single point may be considered a 0-simplex, and a line segment may be considered a 1-simplex. A simplex may be defined as the smallest convex set containing the given vertices.

A regular simplex is a simplex that is also a regular polytope. A regular n-simplex may be constructed from a regular (n − 1)-simplex by connecting a new vertex to all original vertices by the common edge length.

In topology and combinatorics, it is common to “glue together” simplices to form a simplicial complex. The associated combinatorial structure is called an abstract simplicial complex, in which context the word “simplex” simply means any finite set of vertices.

Simplex algorithm

In mathematical optimization, Dantzig's simplex algorithm (or simplex method) is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century.

The name of the algorithm is derived from the concept of a simplex and was suggested by T. S. Motzkin. Simplices are not actually used in the method, but one interpretation of it is that it operates on simplicial cones, and these become proper simplices with an additional constraint. The simplicial cones in question are the corners (i.e., the neighborhoods of the vertices) of a geometric object called a polytope. The shape of this polytope is defined by the constraints applied to the objective function.

Overview

The simplex algorithm operates on linear programs in standard form:

with 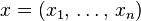the variables of the problem, are the coefficients of the objective function, A is a p×n matrix, and 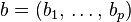constants with 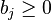. There is a straightforward process to convert any linear program into one in standard form so this results in no loss of generality.

Linear programming

Linear programming (LP; also called linear optimization) is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming (mathematical optimization).

More formally, linear programming is a technique for the optimization of a linear objective function, subject to linear equality and linear inequality constraints. Its feasible region is a convex polytope, which is a set defined as the intersection of finitely many half spaces, each of which is defined by a linear inequality. Its objective function is a real-valued affine (linear) function defined on this polyhedron. A linear programming algorithm finds a point in the polyhedron where this function has the smallest (or largest) value if such a point exists.

Linear programs are problems that can be expressed in canonical form as

where x represents the vector of variables (to be determined), c and b are vectors of (known) coefficients, A is a (known) matrix of coefficients, and is the matrix transpose. The expression to be maximized or minimized is called the objective function (c^Tx in this case). The inequalities Ax ≤ b and x ≥ 0 are the constraints which specify a convex polytope over which the objective function is to be optimized. In this context, two vectors are comparable when they have the same dimensions. If every entry in the first is less-than or equal-to the corresponding entry in the second then we can say the first vector is less-than or equal-to the second vector.