Множина

Множина́ — одне з основних понять сучасної математики. Строго воно не визначається, але може бути дано інтуїтивне визначення множини як сукупності певних і різних об'єктів довільної природи, яка розглядається як одне ціле. Об'єкти, які складають множину, називаються її елементами. Наприклад, можна говорити про множину усіх книг в певній бібліотеці, множину літер українського алфавіту або про множину всіх коренів певного рівняння тощо.

Основні поняття

Множина вважається означеною, якщо про кожен об'єкт, що розглядається, можна казати, що він або належить, або не належить множині. Ідентичні (тобто однакові) об'єкти в множині не допускаються.

На письмі множини позначаються, як правило, великими літерами. Для деяких множин у математиці вживаються сталі позначення. Наприклад:

• ℕ — множина натуральних чисел,
• ℤ — множина цілих чисел,
• ℚ — множина раціональних чисел,
• ℝ — множина дійсних чисел,
• ℂ — множина комплексних чисел.

---

• Нехай А — множина. Той факт, що елемент x входить в множину А, або належить множині А, позначається як x ∈ A. Той факт, що елемент x не входить в множину А, позначається x ∉ A. Знак ∈ називається знаком належності. Він є стилізацією першої літери грецького слова εστι (бути).

• Множина B, всі елементи якої належать множині А, називають підмножиною множини A, або частиною множини А і позначають цей факт символами B ⊆ A, A ⊇ B.

Непуста підмножина B даної множини А, відмінна від множини А, має назву правильної частини (або власної підмножини чи точної підмножини) множини А. Для позначення того факту, що B є підмножиною А, яка не збігається з А, використовують позначки B ⊂ A, A ⊃ B. Знаки ⊆, ⊇, ⊂, ⊃ називаються знаками включення.

Докладніше дивись Підмножина.

• Дві множини А та B є рівними (позначається A = B), коли вони мають однакові елементи.

• В теорії множин виділяють також порожню множину, тобто множину, в яку не входить жоден елемент. Така множина позначається як ∅. Порожня множина є підмножиною будь-якої множини. Також завжди A ⊆ A, що природно, адже кожний елемент множини А належить цій множині.

Докладніше дивись Порожня множина.

Способи задання множин

• Задання множини за допомогою переліку її елементів.

Нехай множина X складається з елементів a, b, c, …, k. Для означення цього факту використовується позначення:

X = {a, b, c, … , k}

A = {4, 2, 1, 3}

B = {червоний, білий, блакитний}

Наприклад, множина натуральних чисел ℕ визначається як:

ℕ = {1, 2, 3, … , n, …}

• Задання множини вказівкою властивості її елементів.

В математичних задачах, як правило, розглядають елементи деякої цілком означеної множини A. При цьому необхідні елементи виділяють за деякою їх властивістю (або вказують породжуючу процедуру) P, такою що кожний елемент x ∈ A або має властивість P (записується P(x)), або не має її. За допомогою властивості P виділимо множину всіх тих елементів, які мають властивість P. Цю множину будемо позначати як {x ∈ A | P(x)} = {x | P(x)}. Задання множини вказівкою її властивості (або породжуючим предикатом) слід здійснювати обережно. Наприклад, множина Y = {X|X∉X} (множина всіх множин, які не містять себе як елемента) веде до парадокса Рассела і є некоректною в аксіоматичній теорії множин.

Операції з множинами

Доповнення та різниця множин

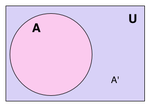
Нехай задана деяка множина U (універсальна множина або універсум). Якщо A ⊂ U, то елементи множини U, які не належать А, називаються доповненням множини А до множини U і позначають як C_UA або U^CA. Якщо A ⊂ U, B ⊂ U, то доповнення множини B до А називають різницею множин А та B (саме в такому порядку) і позначають А \ B або А-B, тобто A \ B = {x: x ∈ A ∧ x ∉ B}.

Різниця множин A та B

Доповнення множини A до U

Примітка: Тут символ ∧ означає вимогу одночасної справедливості обох частин твердження (логічна зв'язка «І», кон'юнкція). Парний з ним символ ∨ означає вимогу справедливості щонайменше одного з двох тверджень (чи обох одночасно) (диз'юнкція, логічне АБО).

Приклади:

• {1, 2} − {червоний, білий} = {1, 2}
• {1, 2, зелений} − {червоний, білий, зелений} = {1, 2}
• {1, 2} − {1, 2} = ∅
• Якщо U — множина цілих чисел, то доповнення її підмножини A всіх парних чисел є підмножина В всіх непарних чисел.

Деякі властивості операції доповнення:

• A ∪ A′ = U
• A ∩ A′ = ∅
• (A′)′ = A
• A − B = A ∩ B′

Об'єднання множин

Об'єднання множин A та B

Об'єднанням множин А та B називається множина, яка складається з усіх тих елементів, які належать хоча б одній з множин A, B:

• A ∪ B = {x: x ∈ A ∨ x ∈ B}.

Приклади:

• {1, 2} ∪ {червоний, білий} = {1, 2, червоний, білий}
• {1, 2, зелений} ∪ {червоний, білий, зелений} = {1, 2, червоний, білий, зелений}
• {1, 2} ∪ {1, 2} = {1, 2}

Деякі властивості операції об'єднання:

• A ∪ B   =   B ∪ A
• A  ⊆  A ∪ B
• A ∪ A   =  A
• A ∪ ∅   =  A

Перетин множин

Перетин множин A та B

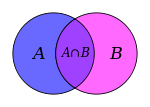
Перетином множин А та B називається множина, яка складається з усіх тих елементів, які належать кожній із множин А, B:

• A ∩ B = {x: x ∈ A ∧ x ∈ B}.

Кажуть, що множини не перетинаються, якщо A ∩ B = ∅

Приклади:

• {1, 2} ∩ {червоний, білий} = ∅
• {1, 2, зелений} ∩ {червоний, білий, зелений} = {зелений}
• {1, 2} ∩ {1, 2} = {1, 2}

Деякі властивості перетину:

• A ∩ B   =   B ∩ A
• A ∩ B   ⊆   A
• A ∩ A   =   A
• A ∩ ∅   =   ∅

Симетрична різниця множин

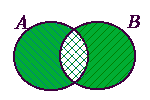
Симетрична різниця множин A та B є така множина елементів, які містяться в одній з цих двох множин, але не в обох. Позначається як AΔB.

Симетрична різниця AΔB

Наприклад, симетрична різниця множин {1,2,3} та {3,4} є {1,2,4}.

Деякі властивості симетричної різниці:

A Δ B = (A − B) ∪(B − A)

A Δ B = (A ∪B) − (A ∩B)

Алгебра множин

Операції ∩, ∪ та доповнення множини утворюють алгебру з певними властивостями.

Потужність множини

Практично всі з розглянутих вище множин має визначену кількість елементів. Наприклад, множина А з розділу «Способи задання множин» має 4 елементи, множина B — три елементи. Порожня множина має нуль елементів. Існують множини, які мають нескінченну кількість елементів. Такою є множина ℕ всіх натуральних чисел. Поняття потужності множин стає важливим в контексті встановлення відношень між множинами. Зрозуміло, наприклад, що взаємооднозначне відношення між множинами А та B можливо встановити лише коли кількість їхніх елементів збігається. Особливо важливою проблема порівняння потужності постає для множин з нескінченною кількістю елементів. Виявляється, що потужності таких множин можуть бути не рівними, і це призводить до деяких цікавих наслідків.

Декартовий добуток множин

Декартовий добуток (прямий декартів добуток) множин X та Y — це множина усіх можливих впорядкованих пар або кортежів, першими компонентами яких є елементи множини X, а другими — елементи множини Y.

Декартовий добуток множин X та Y позначається як X × Y: X × Y = { (x, y) | x ∈ X ∧ y ∈ Y }

Тут впорядкована пара (x, y) елементів x, y є множина {{x}, {x, y}}, яка має таку властивість, що (x, y) ≠ (y, x).

Див. також

• Нотація множин
• Циклічний порядок
• Теорія множин:
  • Інтуїтивна теорія множин
  • Аксіоматична теорія множин
• Алгебра множин
• Операції з множинами:
  • Перетин множин
  • Об'єднання множин
  • Різниця множин
  • Симетрична різниця множин
  • Декартів добуток множин
• Властивості множин
  • Потужність множини
  • Зліченність множин
  • Скінченність множин
• Відповідності між множинами
  • Відповідність між множинами
  • Відношення
  • Відображення
• Парадокси теорії множин
  • Парадокс Рассела
  • Таблиця математичних символів