Aira
Pels articles omonims, veire Aira (omonimia).L’aira es la mesura d'una superfícia. Per metonimia, se designa sovent aquela mesura pel tèrme de superfícia (per exemple, se pòt parlar de l' « aira d'un carrat » o de la « superfícia d'un carrat »).
En matematicas, s'utiliza de preferéncia lo tèrme d'aira (del bas latin aera « espaci plan »).
Lo tèrme de superfícia s'utiliza principalament per de terrens (superfícia d'un jardin, d'un camp) e s'exprimís (dins lo Sistèma Internacional d'Unitats) en mètres carrats (m²) o en d'autras unitats.
Mesuras de l'SI:
Autras mesuras:
Calcul de l'aira[modificar | modificar la font]
Lo calcul d'aira es un domeni ample de las matematicas que va de l'aira de superfícias usualas fins al calcul integral.
Lo calcul de l'aira per de figuras geometricas elementàrias es simple. Los poligòns mai complèxes se pòdon descopar en triangles, e se pòt alara calcular l'aira de cada triangle:
- en geometria euclidiana, l'aira d'un triangle es lo produch de la longor de sa basa per sa nautor, dividit per dos.
Quand se tracta d'una superfícia delimitada per una corba, se pòt far una aproximacion d’aquela corba per un poligòn e aplicar lo metòde çai jos per aver una aproximacion de l'aira; s'aquela corba se pòt definir per una foncion, sufís de calcular l'integrala d’aquela foncion.
Exemples d'airas de figuras planas[modificar | modificar la font]
- Carrat de costat a: a2
- Doncas l'aira val AD · AB = BA · BC = BC · CD = DA · DC
- Rectangle de largor l e de longor L: l · L
- Doncas l'aira val AD · AB = BA · BC = BC · CD = DA · DC
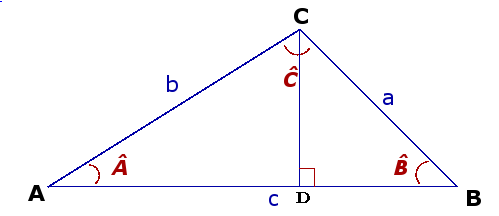
- Triangle de basa b e de nautor h: (b · h) / 2
- Doncas l'aira val (CD · AB) / 2
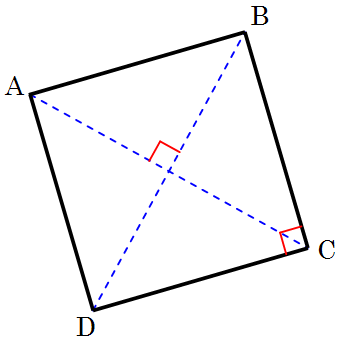
- Lausange de diagonalas a e b: a · b / 2
- Doncas l'aira val AC · BD / 2
- Parallelograma de basa b e de nautor h : b · h
- Doncas l'aira val AB · AH = DC · AH
- Trapèzi de petita basa b, de granda basa B e de nautor H: (b + B) · H / 2
- Doncas l'aira val (AB + DC) · AH / 2
- Cercle de rai r : π · r2
- Ellipsa de semiaxes a e b : π · a · b
