- published: 11 Oct 2015
- views: 5916
Create your page here
-
remove the playlistManifold
- remove the playlistManifold
back to playlist
A visual explanation and definition of manifolds are given. This includes motivations for topology, Hausdorffness and second-countability.
If you want to learn more, check out one of these (or any other basic differential geometry or topology book):
- M. Spivak: "A Comprehensive Introduction to Differential Geometry"
- M. Nakahara: "Geometry, Topology and Physics"
- J. W. Milnor: "Topology from the differentiable viewpoint"
What is an intake manifold? How do intake manifolds work? What is a performance intake manifold? This video features a Skunk2 Pro series intake manifold courtesy of Redline360.com. Intake manifolds are the connection between the throttle body and the cylinder head. They also serve as a hub for connections like the IAT sensor, the EVAP purge valve, the fuel rail, the breather hose, and a vacuum connection for power brakes.
Check out the performance intake manifold from the video here:
Skunk2 Intake Manifold: http://www.redline360.com/skunk2-intake-manifold-acura-integra-ls-gs-rs-non-vtec-307-05-0280
Redline360: http://www.redline360.com
Related Videos:
Gas Pedal - http://youtu.be/smI2ijg4KcM
Power Brakes - http://youtu.be/LThrL8Jjsgc
Please feel free to rate, comment, and subscribe!
And don't forget to check out my Facebook page:
http://www.facebook.com/engineeringexplained
Also check out my official website: Make suggestions, participate in forums, learn through logically ordered lessons, read FAQs, and plan your future!
http://www.howdoesacarwork.com
Now on Twitter:
http://www.twitter.com/jasonfenske13
NEW VIDEO EVERY WEDNESDAY!
- published: 14 Aug 2013
- views: 294926
"Manifolds are a bit like pornography: hard to define, but you know one when you see one."
S. Weinberger
--------------------------------------------------------------------------------
2010 Clay Research Conference
What is a Manifold?
Mikhail Gromov
Clay Mathematics Institute
http://www.claymath.org/video
- published: 26 Nov 2011
- views: 122017
Complete instructions for intake manifold swap on 4.6l Ford V8 engine. It is easy! I got new Dorman 615-175 to replace stock OEM part. Each step was relatively easy but there were a lot of steps. Took me 6 hours total for removal and repair. The Dorman part came with new thermostat and O-ring. Also had new alternator bracket as old one could not be used. This part is improved over original OE as has O-rings for all ports so a gasket is not needed. No more leaking coolant. Fits 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009 and 2010 Crown Victoria and other Ford, Lincoln, Mercury V8 motors such as Mustang, Explorer, Expedition, Grand Marquis, Town Car. The 5.4l truck and Expedition should be similar.
- published: 10 Apr 2014
- views: 196300
The installation of the manifold is an integral stage of a heating system. The JG Speedfit manifold kits can be used on either underfloor heating or radiator based systems.
Manifolds consist of two rails; one for the flow and one for the return, complete with ball valves and drain / filling valves.
JG speedfit manifolds are complete with pre-fitted brackets and vibration isolation mounts.
They are available to buy online at www.tradingdepot.co.uk
- published: 14 Feb 2013
- views: 423431
Se muestra como sacar el manómetro sin tan alta presión. Mas seguro, sin tanta suciedad, ni el peligro de que nos queme el frío o el aceite.
- published: 04 Nov 2014
- views: 72910
These are the tools I have found to work when extracting broken studs-
Basic Black Oxide drill bits used-
http://www.amazon.com/gp/product/B003BWNGNM/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B003BWNGNM&linkCode;=as2&tag;=fordt-20&linkId;=CGMAG5KISYURV6V2
Upgraded Titanium Nitride Coated drill bits for not much more-
http://www.amazon.com/gp/product/B000FSSIYW/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000FSSIYW&linkCode;=as2&tag;=fordt-20&linkId;=NXJYEEG5GWEGXE63
Micro Extractor set-(in case the stud spins in deeper during drilling)
http://www.amazon.com/gp/product/B000Q60UOO/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000Q60UOO&linkCode;=as2&tag;=fordt-20&linkId;=EJKD42FK2NWVYJZL
Standard Extractor set-
http://www.amazon.com/gp/product/B001A4CWHO/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B001A4CWHO&linkCode;=as2&tag;=fordt-20&linkId;=XD2VVLNXSWMVZOFL
Compact right angle Drill-
http://www.amazon.com/gp/product/B0002SROQS/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B0002SROQS&linkCode;=as2&tag;=fordt-20&linkId;=O3PBYG7IJC24NNYV
Mapp Oxygen Torch Kit I used-
http://www.amazon.com/gp/product/B00BJR0O5O/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B00BJR0O5O&linkCode;=as2&tag;=fordt-20&linkId;=BVHPFQJXZRHP64AY
Kroil Oil for tough frozen studs-
http://www.amazon.com/gp/product/B000F09CEA/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000F09CEA&linkCode;=as2&tag;=fordt-20&linkId;=POX5Q6W7HXSS2L6X
Original Exhaust Manifold replacement video-
https://www.youtube.com/watch?v=2ZpkvRsNwYQ
Final drill bit length that works on 4.6l 3v Engines:
1/16 BIT- 47MM
5/64 BIT- 42MM
3/32 BIT- 39MM
7/64 BIT- 42MM
1/8 BIT- 38MM
Please consider supporting the future production of helpful videos like this:
https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted;_button_id=URAPZQ4MLXP3C
Check us out-
Facebook: http://www.facebook.com/FordTechMakuloco
Twitter: http://twitter.com/FordTechMak
Instagram: http://instagram.com/fordtechmakuloco/
My company YouTube Channel- BSG Automotive providing repair advice on makes and models other than Ford: http://www.youtube.com/c/BSGAutomotive1
- published: 14 Dec 2015
- views: 49746
Manifold
In mathematics, a manifold is a topological space that resembles Euclidean space near each point. More precisely, each point of an n-dimensional manifold has a neighbourhood that is homeomorphic to the Euclidean space of dimension n.
One-dimensional manifolds include lines and circles, but not figure eights (because they have singularities called crossing points). Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, which can all be embedded (formed without self-intersections) in three dimensional real space, but also the Klein bottle and real projective plane which cannot.
Although a manifold resembles Euclidean space near each point, globally it may not. For example, the surface of the sphere is not a Euclidean space, but in a region it can be charted by means of map projections of the region into the Euclidean plane (in the context of manifolds they are called charts). When a region appears in two neighbouring charts, the two representations do not coincide exactly and a transformation is needed to pass from one to the other, called a transition map.
This page contains text from Wikipedia, the Free Encyclopedia -
http://wn.com/Manifold
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...
-
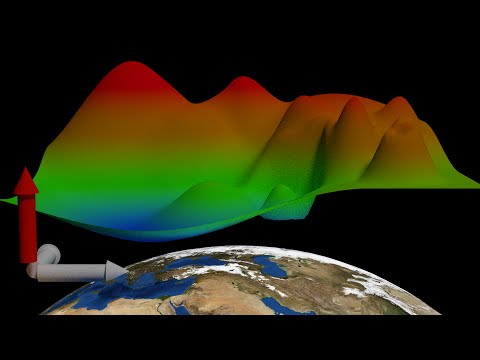3:51What is a manifold?
What is a manifold?What is a manifold?
A visual explanation and definition of manifolds are given. This includes motivations for topology, Hausdorffness and second-countability. If you want to learn more, check out one of these (or any other basic differential geometry or topology book): - M. Spivak: "A Comprehensive Introduction to Differential Geometry" - M. Nakahara: "Geometry, Topology and Physics" - J. W. Milnor: "Topology from the differentiable viewpoint" -
6:27Intake Manifold - Explained
Intake Manifold - ExplainedIntake Manifold - Explained
What is an intake manifold? How do intake manifolds work? What is a performance intake manifold? This video features a Skunk2 Pro series intake manifold courtesy of Redline360.com. Intake manifolds are the connection between the throttle body and the cylinder head. They also serve as a hub for connections like the IAT sensor, the EVAP purge valve, the fuel rail, the breather hose, and a vacuum connection for power brakes. Check out the performance intake manifold from the video here: Skunk2 Intake Manifold: http://www.redline360.com/skunk2-intake-manifold-acura-integra-ls-gs-rs-non-vtec-307-05-0280 Redline360: http://www.redline360.com Related Videos: Gas Pedal - http://youtu.be/smI2ijg4KcM Power Brakes - http://youtu.be/LThrL8Jjsgc Please feel free to rate, comment, and subscribe! And don't forget to check out my Facebook page: http://www.facebook.com/engineeringexplained Also check out my official website: Make suggestions, participate in forums, learn through logically ordered lessons, read FAQs, and plan your future! http://www.howdoesacarwork.com Now on Twitter: http://www.twitter.com/jasonfenske13 NEW VIDEO EVERY WEDNESDAY! -
53:56What is a Manifold? - Mikhail Gromov
What is a Manifold? - Mikhail GromovWhat is a Manifold? - Mikhail Gromov
"Manifolds are a bit like pornography: hard to define, but you know one when you see one." S. Weinberger -------------------------------------------------------------------------------- 2010 Clay Research Conference What is a Manifold? Mikhail Gromov Clay Mathematics Institute http://www.claymath.org/video -
12:43Building A Turbo Manifold
Building A Turbo Manifold -
8:27Intake Manifold Cleaning And Removing Carbon
Intake Manifold Cleaning And Removing Carbon -
26:23Ford 4.6L V8 Intake Manifold Replacement
Ford 4.6L V8 Intake Manifold ReplacementFord 4.6L V8 Intake Manifold Replacement
Complete instructions for intake manifold swap on 4.6l Ford V8 engine. It is easy! I got new Dorman 615-175 to replace stock OEM part. Each step was relatively easy but there were a lot of steps. Took me 6 hours total for removal and repair. The Dorman part came with new thermostat and O-ring. Also had new alternator bracket as old one could not be used. This part is improved over original OE as has O-rings for all ports so a gasket is not needed. No more leaking coolant. Fits 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009 and 2010 Crown Victoria and other Ford, Lincoln, Mercury V8 motors such as Mustang, Explorer, Expedition, Grand Marquis, Town Car. The 5.4l truck and Expedition should be similar. -
8:47Installing the JG Speedfit Underfloor Heating Manifold
Installing the JG Speedfit Underfloor Heating ManifoldInstalling the JG Speedfit Underfloor Heating Manifold
The installation of the manifold is an integral stage of a heating system. The JG Speedfit manifold kits can be used on either underfloor heating or radiator based systems. Manifolds consist of two rails; one for the flow and one for the return, complete with ball valves and drain / filling valves. JG speedfit manifolds are complete with pre-fitted brackets and vibration isolation mounts. They are available to buy online at www.tradingdepot.co.uk -
20:36Removing Broken Exhaust Manifold Bolts - Hemi Dodge Ram
Removing Broken Exhaust Manifold Bolts - Hemi Dodge Ram -
0:37R410A - COMO QUITAR MANIFOLD
R410A - COMO QUITAR MANIFOLDR410A - COMO QUITAR MANIFOLD
Se muestra como sacar el manómetro sin tan alta presión. Mas seguro, sin tanta suciedad, ni el peligro de que nos queme el frío o el aceite. -
23:45Ford 4.6L 5.4L 6.8L 3v Engines: Broken Exhaust Manifold Stud Removal
Ford 4.6L 5.4L 6.8L 3v Engines: Broken Exhaust Manifold Stud RemovalFord 4.6L 5.4L 6.8L 3v Engines: Broken Exhaust Manifold Stud Removal
These are the tools I have found to work when extracting broken studs- Basic Black Oxide drill bits used- http://www.amazon.com/gp/product/B003BWNGNM/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B003BWNGNM&linkCode;=as2&tag;=fordt-20&linkId;=CGMAG5KISYURV6V2 Upgraded Titanium Nitride Coated drill bits for not much more- http://www.amazon.com/gp/product/B000FSSIYW/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000FSSIYW&linkCode;=as2&tag;=fordt-20&linkId;=NXJYEEG5GWEGXE63 Micro Extractor set-(in case the stud spins in deeper during drilling) http://www.amazon.com/gp/product/B000Q60UOO/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000Q60UOO&linkCode;=as2&tag;=fordt-20&linkId;=EJKD42FK2NWVYJZL Standard Extractor set- http://www.amazon.com/gp/product/B001A4CWHO/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B001A4CWHO&linkCode;=as2&tag;=fordt-20&linkId;=XD2VVLNXSWMVZOFL Compact right angle Drill- http://www.amazon.com/gp/product/B0002SROQS/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B0002SROQS&linkCode;=as2&tag;=fordt-20&linkId;=O3PBYG7IJC24NNYV Mapp Oxygen Torch Kit I used- http://www.amazon.com/gp/product/B00BJR0O5O/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B00BJR0O5O&linkCode;=as2&tag;=fordt-20&linkId;=BVHPFQJXZRHP64AY Kroil Oil for tough frozen studs- http://www.amazon.com/gp/product/B000F09CEA/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000F09CEA&linkCode;=as2&tag;=fordt-20&linkId;=POX5Q6W7HXSS2L6X Original Exhaust Manifold replacement video- https://www.youtube.com/watch?v=2ZpkvRsNwYQ Final drill bit length that works on 4.6l 3v Engines: 1/16 BIT- 47MM 5/64 BIT- 42MM 3/32 BIT- 39MM 7/64 BIT- 42MM 1/8 BIT- 38MM Please consider supporting the future production of helpful videos like this: https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted;_button_id=URAPZQ4MLXP3C Check us out- Facebook: http://www.facebook.com/FordTechMakuloco Twitter: http://twitter.com/FordTechMak Instagram: http://instagram.com/fordtechmakuloco/ My company YouTube Channel- BSG Automotive providing repair advice on makes and models other than Ford: http://www.youtube.com/c/BSGAutomotive1
Manifold
ALBUMS
- X-Ray Attraction released: 2005
X-Ray Attraction
Released 2005- add to main playlist Play in Full Screen Time for the Heist
- add to main playlist Play in Full Screen Tomahawk
- add to main playlist Play in Full Screen Intrusion
- add to main playlist Play in Full Screen Barrel Night
- add to main playlist Play in Full Screen The Wolf
- add to main playlist Play in Full Screen Find Your Pokemon
- add to main playlist Play in Full Screen Invited Session
- add to main playlist Play in Full Screen Christmas
- add to main playlist Play in Full Screen Abstract Dimensions
-
What is a manifold?
A visual explanation and definition of manifolds are given. This includes motivations for topology, Hausdorffness and second-countability. If you want to learn more, check out one of these (or any other basic differential geometry or topology book): - M. Spivak: "A Comprehensive Introduction to Differential Geometry" - M. Nakahara: "Geometry, Topology and Physics" - J. W. Milnor: "Topology from the differentiable viewpoint" -
Intake Manifold - Explained
What is an intake manifold? How do intake manifolds work? What is a performance intake manifold? This video features a Skunk2 Pro series intake manifold courtesy of Redline360.com. Intake manifolds are the connection between the throttle body and the cylinder head. They also serve as a hub for connections like the IAT sensor, the EVAP purge valve, the fuel rail, the breather hose, and a vacuum connection for power brakes. Check out the performance intake manifold from the video here: Skunk2 Intake Manifold: http://www.redline360.com/skunk2-intake-manifold-acura-integra-ls-gs-rs-non-vtec-307-05-0280 Redline360: http://www.redline360.com Related Videos: Gas Pedal - http://youtu.be/smI2ijg4KcM Power Brakes - http://youtu.be/LThrL8Jjsgc Please feel free to rate, comment, and subscribe! And... -
What is a Manifold? - Mikhail Gromov
"Manifolds are a bit like pornography: hard to define, but you know one when you see one." S. Weinberger -------------------------------------------------------------------------------- 2010 Clay Research Conference What is a Manifold? Mikhail Gromov Clay Mathematics Institute http://www.claymath.org/video -
-
-
Ford 4.6L V8 Intake Manifold Replacement
Complete instructions for intake manifold swap on 4.6l Ford V8 engine. It is easy! I got new Dorman 615-175 to replace stock OEM part. Each step was relatively easy but there were a lot of steps. Took me 6 hours total for removal and repair. The Dorman part came with new thermostat and O-ring. Also had new alternator bracket as old one could not be used. This part is improved over original OE as has O-rings for all ports so a gasket is not needed. No more leaking coolant. Fits 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009 and 2010 Crown Victoria and other Ford, Lincoln, Mercury V8 motors such as Mustang, Explorer, Expedition, Grand Marquis, Town Car. The 5.4l truck and Expedition should be similar. -
Installing the JG Speedfit Underfloor Heating Manifold
The installation of the manifold is an integral stage of a heating system. The JG Speedfit manifold kits can be used on either underfloor heating or radiator based systems. Manifolds consist of two rails; one for the flow and one for the return, complete with ball valves and drain / filling valves. JG speedfit manifolds are complete with pre-fitted brackets and vibration isolation mounts. They are available to buy online at www.tradingdepot.co.uk -
-
R410A - COMO QUITAR MANIFOLD
Se muestra como sacar el manómetro sin tan alta presión. Mas seguro, sin tanta suciedad, ni el peligro de que nos queme el frío o el aceite. -
Ford 4.6L 5.4L 6.8L 3v Engines: Broken Exhaust Manifold Stud Removal
These are the tools I have found to work when extracting broken studs- Basic Black Oxide drill bits used- http://www.amazon.com/gp/product/B003BWNGNM/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B003BWNGNM&linkCode;=as2&tag;=fordt-20&linkId;=CGMAG5KISYURV6V2 Upgraded Titanium Nitride Coated drill bits for not much more- http://www.amazon.com/gp/product/B000FSSIYW/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000FSSIYW&linkCode;=as2&tag;=fordt-20&linkId;=NXJYEEG5GWEGXE63 Micro Extractor set-(in case the stud spins in deeper during drilling) http://www.amazon.com/gp/product/B000Q60UOO/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000Q60UOO&linkCode;=as2&tag;=fordt-20&linkId;=EJKD42FK2NWVYJZL Standard Extractor set- http://www.amazon.com/gp/product/B001A4CW...
What is a manifold?
- Order: Reorder
- Duration: 3:51
- Updated: 11 Oct 2015
- views: 5916
A visual explanation and definition of manifolds are given. This includes motivations for topology, Hausdorffness and second-countability.
If you want to learn...
A visual explanation and definition of manifolds are given. This includes motivations for topology, Hausdorffness and second-countability.
If you want to learn more, check out one of these (or any other basic differential geometry or topology book):
- M. Spivak: "A Comprehensive Introduction to Differential Geometry"
- M. Nakahara: "Geometry, Topology and Physics"
- J. W. Milnor: "Topology from the differentiable viewpoint"
wn.com/What Is A Manifold
A visual explanation and definition of manifolds are given. This includes motivations for topology, Hausdorffness and second-countability.
If you want to learn more, check out one of these (or any other basic differential geometry or topology book):
- M. Spivak: "A Comprehensive Introduction to Differential Geometry"
- M. Nakahara: "Geometry, Topology and Physics"
- J. W. Milnor: "Topology from the differentiable viewpoint"
- published: 11 Oct 2015
- views: 5916
Intake Manifold - Explained
- Order: Reorder
- Duration: 6:27
- Updated: 14 Aug 2013
- views: 294926
What is an intake manifold? How do intake manifolds work? What is a performance intake manifold? This video features a Skunk2 Pro series intake manifold courtes...
What is an intake manifold? How do intake manifolds work? What is a performance intake manifold? This video features a Skunk2 Pro series intake manifold courtesy of Redline360.com. Intake manifolds are the connection between the throttle body and the cylinder head. They also serve as a hub for connections like the IAT sensor, the EVAP purge valve, the fuel rail, the breather hose, and a vacuum connection for power brakes.
Check out the performance intake manifold from the video here:
Skunk2 Intake Manifold: http://www.redline360.com/skunk2-intake-manifold-acura-integra-ls-gs-rs-non-vtec-307-05-0280
Redline360: http://www.redline360.com
Related Videos:
Gas Pedal - http://youtu.be/smI2ijg4KcM
Power Brakes - http://youtu.be/LThrL8Jjsgc
Please feel free to rate, comment, and subscribe!
And don't forget to check out my Facebook page:
http://www.facebook.com/engineeringexplained
Also check out my official website: Make suggestions, participate in forums, learn through logically ordered lessons, read FAQs, and plan your future!
http://www.howdoesacarwork.com
Now on Twitter:
http://www.twitter.com/jasonfenske13
NEW VIDEO EVERY WEDNESDAY!
wn.com/Intake Manifold Explained
What is an intake manifold? How do intake manifolds work? What is a performance intake manifold? This video features a Skunk2 Pro series intake manifold courtesy of Redline360.com. Intake manifolds are the connection between the throttle body and the cylinder head. They also serve as a hub for connections like the IAT sensor, the EVAP purge valve, the fuel rail, the breather hose, and a vacuum connection for power brakes.
Check out the performance intake manifold from the video here:
Skunk2 Intake Manifold: http://www.redline360.com/skunk2-intake-manifold-acura-integra-ls-gs-rs-non-vtec-307-05-0280
Redline360: http://www.redline360.com
Related Videos:
Gas Pedal - http://youtu.be/smI2ijg4KcM
Power Brakes - http://youtu.be/LThrL8Jjsgc
Please feel free to rate, comment, and subscribe!
And don't forget to check out my Facebook page:
http://www.facebook.com/engineeringexplained
Also check out my official website: Make suggestions, participate in forums, learn through logically ordered lessons, read FAQs, and plan your future!
http://www.howdoesacarwork.com
Now on Twitter:
http://www.twitter.com/jasonfenske13
NEW VIDEO EVERY WEDNESDAY!
- published: 14 Aug 2013
- views: 294926
What is a Manifold? - Mikhail Gromov
- Order: Reorder
- Duration: 53:56
- Updated: 26 Nov 2011
- views: 122017
"Manifolds are a bit like pornography: hard to define, but you know one when you see one."
S. Weinberger
---------------------------------------------------...
"Manifolds are a bit like pornography: hard to define, but you know one when you see one."
S. Weinberger
--------------------------------------------------------------------------------
2010 Clay Research Conference
What is a Manifold?
Mikhail Gromov
Clay Mathematics Institute
http://www.claymath.org/video
wn.com/What Is A Manifold Mikhail Gromov
"Manifolds are a bit like pornography: hard to define, but you know one when you see one."
S. Weinberger
--------------------------------------------------------------------------------
2010 Clay Research Conference
What is a Manifold?
Mikhail Gromov
Clay Mathematics Institute
http://www.claymath.org/video
- published: 26 Nov 2011
- views: 122017
Building A Turbo Manifold
- Order: Reorder
- Duration: 12:43
- Updated: 12 Feb 2016
- views: 87726
Give me some feedback on this video! let me know if you guys learned anything!!
Need custom parts?
Dm @Iamdan6598 on instagram for details!
Wanna send to my p....
Give me some feedback on this video! let me know if you guys learned anything!!
Need custom parts?
Dm @Iamdan6598 on instagram for details!
Wanna send to my p.o box?
PO BOX:PO Box 581 Torrington, CT 06790-0581
wn.com/Building A Turbo Manifold
Intake Manifold Cleaning And Removing Carbon
- Order: Reorder
- Duration: 8:27
- Updated: 30 Oct 2013
- views: 530049
This video will show you an easy way to clean ANY dirty (CARBON built up) on aluminum intake. Please DON'T try this on plastic intake, Injoy the video :)
This video will show you an easy way to clean ANY dirty (CARBON built up) on aluminum intake. Please DON'T try this on plastic intake, Injoy the video :)
wn.com/Intake Manifold Cleaning And Removing Carbon
Ford 4.6L V8 Intake Manifold Replacement
- Order: Reorder
- Duration: 26:23
- Updated: 10 Apr 2014
- views: 196300
Complete instructions for intake manifold swap on 4.6l Ford V8 engine. It is easy! I got new Dorman 615-175 to replace stock OEM part. Each step was relatively ...
Complete instructions for intake manifold swap on 4.6l Ford V8 engine. It is easy! I got new Dorman 615-175 to replace stock OEM part. Each step was relatively easy but there were a lot of steps. Took me 6 hours total for removal and repair. The Dorman part came with new thermostat and O-ring. Also had new alternator bracket as old one could not be used. This part is improved over original OE as has O-rings for all ports so a gasket is not needed. No more leaking coolant. Fits 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009 and 2010 Crown Victoria and other Ford, Lincoln, Mercury V8 motors such as Mustang, Explorer, Expedition, Grand Marquis, Town Car. The 5.4l truck and Expedition should be similar.
wn.com/Ford 4.6L V8 Intake Manifold Replacement
Complete instructions for intake manifold swap on 4.6l Ford V8 engine. It is easy! I got new Dorman 615-175 to replace stock OEM part. Each step was relatively easy but there were a lot of steps. Took me 6 hours total for removal and repair. The Dorman part came with new thermostat and O-ring. Also had new alternator bracket as old one could not be used. This part is improved over original OE as has O-rings for all ports so a gasket is not needed. No more leaking coolant. Fits 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009 and 2010 Crown Victoria and other Ford, Lincoln, Mercury V8 motors such as Mustang, Explorer, Expedition, Grand Marquis, Town Car. The 5.4l truck and Expedition should be similar.
- published: 10 Apr 2014
- views: 196300
Installing the JG Speedfit Underfloor Heating Manifold
- Order: Reorder
- Duration: 8:47
- Updated: 14 Feb 2013
- views: 423431
The installation of the manifold is an integral stage of a heating system. The JG Speedfit manifold kits can be used on either underfloor heating or radiator ba...
The installation of the manifold is an integral stage of a heating system. The JG Speedfit manifold kits can be used on either underfloor heating or radiator based systems.
Manifolds consist of two rails; one for the flow and one for the return, complete with ball valves and drain / filling valves.
JG speedfit manifolds are complete with pre-fitted brackets and vibration isolation mounts.
They are available to buy online at www.tradingdepot.co.uk
wn.com/Installing The Jg Speedfit Underfloor Heating Manifold
The installation of the manifold is an integral stage of a heating system. The JG Speedfit manifold kits can be used on either underfloor heating or radiator based systems.
Manifolds consist of two rails; one for the flow and one for the return, complete with ball valves and drain / filling valves.
JG speedfit manifolds are complete with pre-fitted brackets and vibration isolation mounts.
They are available to buy online at www.tradingdepot.co.uk
- published: 14 Feb 2013
- views: 423431
Removing Broken Exhaust Manifold Bolts - Hemi Dodge Ram
- Order: Reorder
- Duration: 20:36
- Updated: 17 Jan 2015
- views: 105422
In this video I show you how to remove 4 broken exhaust manifold bolts in this 2010 Ram with a 5.7 hemi with out a drill.
Wanna see the manifold installation? ...
In this video I show you how to remove 4 broken exhaust manifold bolts in this 2010 Ram with a 5.7 hemi with out a drill.
Wanna see the manifold installation? Here is the link to that : https://www.youtube.com/watch?v=z-giGgE13Ss
wn.com/Removing Broken Exhaust Manifold Bolts Hemi Dodge Ram
R410A - COMO QUITAR MANIFOLD
- Order: Reorder
- Duration: 0:37
- Updated: 04 Nov 2014
- views: 72910
Se muestra como sacar el manómetro sin tan alta presión. Mas seguro, sin tanta suciedad, ni el peligro de que nos queme el frío o el aceite.
Se muestra como sacar el manómetro sin tan alta presión. Mas seguro, sin tanta suciedad, ni el peligro de que nos queme el frío o el aceite.
wn.com/R410A Como Quitar Manifold
Se muestra como sacar el manómetro sin tan alta presión. Mas seguro, sin tanta suciedad, ni el peligro de que nos queme el frío o el aceite.
- published: 04 Nov 2014
- views: 72910
Ford 4.6L 5.4L 6.8L 3v Engines: Broken Exhaust Manifold Stud Removal
- Order: Reorder
- Duration: 23:45
- Updated: 14 Dec 2015
- views: 49746
These are the tools I have found to work when extracting broken studs-
Basic Black Oxide drill bits used-
http://www.amazon.com/gp/product/B003BWNGNM/ref=as_li_...
These are the tools I have found to work when extracting broken studs-
Basic Black Oxide drill bits used-
http://www.amazon.com/gp/product/B003BWNGNM/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B003BWNGNM&linkCode;=as2&tag;=fordt-20&linkId;=CGMAG5KISYURV6V2
Upgraded Titanium Nitride Coated drill bits for not much more-
http://www.amazon.com/gp/product/B000FSSIYW/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000FSSIYW&linkCode;=as2&tag;=fordt-20&linkId;=NXJYEEG5GWEGXE63
Micro Extractor set-(in case the stud spins in deeper during drilling)
http://www.amazon.com/gp/product/B000Q60UOO/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000Q60UOO&linkCode;=as2&tag;=fordt-20&linkId;=EJKD42FK2NWVYJZL
Standard Extractor set-
http://www.amazon.com/gp/product/B001A4CWHO/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B001A4CWHO&linkCode;=as2&tag;=fordt-20&linkId;=XD2VVLNXSWMVZOFL
Compact right angle Drill-
http://www.amazon.com/gp/product/B0002SROQS/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B0002SROQS&linkCode;=as2&tag;=fordt-20&linkId;=O3PBYG7IJC24NNYV
Mapp Oxygen Torch Kit I used-
http://www.amazon.com/gp/product/B00BJR0O5O/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B00BJR0O5O&linkCode;=as2&tag;=fordt-20&linkId;=BVHPFQJXZRHP64AY
Kroil Oil for tough frozen studs-
http://www.amazon.com/gp/product/B000F09CEA/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000F09CEA&linkCode;=as2&tag;=fordt-20&linkId;=POX5Q6W7HXSS2L6X
Original Exhaust Manifold replacement video-
https://www.youtube.com/watch?v=2ZpkvRsNwYQ
Final drill bit length that works on 4.6l 3v Engines:
1/16 BIT- 47MM
5/64 BIT- 42MM
3/32 BIT- 39MM
7/64 BIT- 42MM
1/8 BIT- 38MM
Please consider supporting the future production of helpful videos like this:
https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted;_button_id=URAPZQ4MLXP3C
Check us out-
Facebook: http://www.facebook.com/FordTechMakuloco
Twitter: http://twitter.com/FordTechMak
Instagram: http://instagram.com/fordtechmakuloco/
My company YouTube Channel- BSG Automotive providing repair advice on makes and models other than Ford: http://www.youtube.com/c/BSGAutomotive1
wn.com/Ford 4.6L 5.4L 6.8L 3V Engines Broken Exhaust Manifold Stud Removal
These are the tools I have found to work when extracting broken studs-
Basic Black Oxide drill bits used-
http://www.amazon.com/gp/product/B003BWNGNM/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B003BWNGNM&linkCode;=as2&tag;=fordt-20&linkId;=CGMAG5KISYURV6V2
Upgraded Titanium Nitride Coated drill bits for not much more-
http://www.amazon.com/gp/product/B000FSSIYW/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000FSSIYW&linkCode;=as2&tag;=fordt-20&linkId;=NXJYEEG5GWEGXE63
Micro Extractor set-(in case the stud spins in deeper during drilling)
http://www.amazon.com/gp/product/B000Q60UOO/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000Q60UOO&linkCode;=as2&tag;=fordt-20&linkId;=EJKD42FK2NWVYJZL
Standard Extractor set-
http://www.amazon.com/gp/product/B001A4CWHO/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B001A4CWHO&linkCode;=as2&tag;=fordt-20&linkId;=XD2VVLNXSWMVZOFL
Compact right angle Drill-
http://www.amazon.com/gp/product/B0002SROQS/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B0002SROQS&linkCode;=as2&tag;=fordt-20&linkId;=O3PBYG7IJC24NNYV
Mapp Oxygen Torch Kit I used-
http://www.amazon.com/gp/product/B00BJR0O5O/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B00BJR0O5O&linkCode;=as2&tag;=fordt-20&linkId;=BVHPFQJXZRHP64AY
Kroil Oil for tough frozen studs-
http://www.amazon.com/gp/product/B000F09CEA/ref=as_li_tl?ie=UTF8&camp;=1789&creative;=390957&creativeASIN;=B000F09CEA&linkCode;=as2&tag;=fordt-20&linkId;=POX5Q6W7HXSS2L6X
Original Exhaust Manifold replacement video-
https://www.youtube.com/watch?v=2ZpkvRsNwYQ
Final drill bit length that works on 4.6l 3v Engines:
1/16 BIT- 47MM
5/64 BIT- 42MM
3/32 BIT- 39MM
7/64 BIT- 42MM
1/8 BIT- 38MM
Please consider supporting the future production of helpful videos like this:
https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted;_button_id=URAPZQ4MLXP3C
Check us out-
Facebook: http://www.facebook.com/FordTechMakuloco
Twitter: http://twitter.com/FordTechMak
Instagram: http://instagram.com/fordtechmakuloco/
My company YouTube Channel- BSG Automotive providing repair advice on makes and models other than Ford: http://www.youtube.com/c/BSGAutomotive1
- published: 14 Dec 2015
- views: 49746
close fullscreen
- Playlist
- Chat
close fullscreen
- Playlist
- Chat
3:51
What is a manifold?
A visual explanation and definition of manifolds are given. This includes motivations for ...
published: 11 Oct 2015
What is a manifold?
What is a manifold?
- Report rights infringement
- published: 11 Oct 2015
- views: 5916
6:27
Intake Manifold - Explained
What is an intake manifold? How do intake manifolds work? What is a performance intake man...
published: 14 Aug 2013
Intake Manifold - Explained
Intake Manifold - Explained
- Report rights infringement
- published: 14 Aug 2013
- views: 294926
53:56
What is a Manifold? - Mikhail Gromov
"Manifolds are a bit like pornography: hard to define, but you know one when you see one."...
published: 26 Nov 2011
What is a Manifold? - Mikhail Gromov
What is a Manifold? - Mikhail Gromov
- Report rights infringement
- published: 26 Nov 2011
- views: 122017
12:43
Building A Turbo Manifold
Give me some feedback on this video! let me know if you guys learned anything!!
Need custo...
published: 12 Feb 2016
Building A Turbo Manifold
Building A Turbo Manifold
- Report rights infringement
- published: 12 Feb 2016
- views: 87726
8:27
Intake Manifold Cleaning And Removing Carbon
This video will show you an easy way to clean ANY dirty (CARBON built up) on aluminum inta...
published: 30 Oct 2013
Intake Manifold Cleaning And Removing Carbon
Intake Manifold Cleaning And Removing Carbon
- Report rights infringement
- published: 30 Oct 2013
- views: 530049
26:23
Ford 4.6L V8 Intake Manifold Replacement
Complete instructions for intake manifold swap on 4.6l Ford V8 engine. It is easy! I got n...
published: 10 Apr 2014
Ford 4.6L V8 Intake Manifold Replacement
Ford 4.6L V8 Intake Manifold Replacement
- Report rights infringement
- published: 10 Apr 2014
- views: 196300
8:47
Installing the JG Speedfit Underfloor Heating Manifold
The installation of the manifold is an integral stage of a heating system. The JG Speedfit...
published: 14 Feb 2013
Installing the JG Speedfit Underfloor Heating Manifold
Installing the JG Speedfit Underfloor Heating Manifold
- Report rights infringement
- published: 14 Feb 2013
- views: 423431
20:36
Removing Broken Exhaust Manifold Bolts - Hemi Dodge Ram
In this video I show you how to remove 4 broken exhaust manifold bolts in this 2010 Ram wi...
published: 17 Jan 2015
Removing Broken Exhaust Manifold Bolts - Hemi Dodge Ram
Removing Broken Exhaust Manifold Bolts - Hemi Dodge Ram
- Report rights infringement
- published: 17 Jan 2015
- views: 105422
0:37
R410A - COMO QUITAR MANIFOLD
Se muestra como sacar el manómetro sin tan alta presión. Mas seguro, sin tanta suciedad, n...
published: 04 Nov 2014
R410A - COMO QUITAR MANIFOLD
R410A - COMO QUITAR MANIFOLD
- Report rights infringement
- published: 04 Nov 2014
- views: 72910
23:45
Ford 4.6L 5.4L 6.8L 3v Engines: Broken Exhaust Manifold Stud Removal
These are the tools I have found to work when extracting broken studs-
Basic Black Oxide d...
published: 14 Dec 2015
Ford 4.6L 5.4L 6.8L 3v Engines: Broken Exhaust Manifold Stud Removal
Ford 4.6L 5.4L 6.8L 3v Engines: Broken Exhaust Manifold Stud Removal
- Report rights infringement
- published: 14 Dec 2015
- views: 49746
What is a manifold?...
Intake Manifold - Explained...
What is a Manifold? - Mikhail Gromov...
Building A Turbo Manifold...
Intake Manifold Cleaning And Removing Carbon...
Ford 4.6L V8 Intake Manifold Replacement...
Installing the JG Speedfit Underfloor Heating Mani...
Removing Broken Exhaust Manifold Bolts - Hemi Dodg...
R410A - COMO QUITAR MANIFOLD...
Ford 4.6L 5.4L 6.8L 3v Engines: Broken Exhaust Man...
-
Lyrics list:lyrics
-
Supernova
Supernova
Supernova
Million years the time has come
Million years are on the ground
The stars are always there at night
Shining on the earth so bright
Endless systems in the space
Endless silence around this place
Million years the time has come
photo: UN / UN
Chilcot's blind spot: Iraq War report buries oil evidence, fails to address motive
Edit Open Democracy 07 Jul 2016
The long-awaited Chilcot Report was finally released today, examining the UK’s involvement in the Iraq War and occupation. Unfortunately, on the most important question, the report’s conclusions are all but silent. why did the UK go to war? ... He shows a remarkable lack of curiosity about the political factors behind the move to war, especially given the weakness (even at the time) of the WMD case ... Most important of these is oil....
photo: AP / Gerald Herbert
New US police shooting in Minnesota as protests continue in Baton Rouge
Edit BBC News 07 Jul 2016
A black man has been shot dead by police in the US state of Minnesota as protests continued over the police killing of a black man in Louisiana. Philando Castile was shot in his car as he reached for his driving licence, his girlfriend said in a Facebook Live video taken during the aftermath. It follows the death of Alton Sterling, who was shot dead by police during an incident in Baton Rouge on Tuesday ... Getty Images. ....
photo: AP / Matt Dunham
Theresa May, Andrea Leadsom To Contest For Tory Leadership, Prime Minister
Edit WorldNews.com 07 Jul 2016
Not since Margaret Thatcher has Britain been led by a woman prime minister, but now that Michael Gove has been eliminated in the second round of the Conservative leadership contest, a woman will once again take on that role, The Independent reported Thursday.Home Secretary Theresa May or Energy Minister Andrea Leadsom will step forward as the country’s newest prime minister in nine weeks’ time....
photo: AP / Wong Maye-E
US sanctions North Korea's Kim Jong-un for rights abuses
Edit The Oslo Times 07 Jul 2016
July 7, Washington. The United States government has imposed sanctions on North Korean leader Kim Jong-un for the first time, accusing him of human rights abuses. A statement from the US Treasury named Kim as directly responsible for violations in his country ... The Oslo Times International News Network ....
photo: NASA / Stephanie Stoll
NASA gets hacked, porn tweeted on official Twitter account
Edit Deccan Chronicle 07 Jul 2016
Seeing a pornographic content may be a warm and exciting welcome for a few, but definitely not when it is cited on an official site of a brand as big as NASA. Yes, NASA’s official Twitter handle for Kepler and K2 was hacked and the hacker left after replacing the profile photo with a woman’s pic, renamed the account name and also tweeted a photo of a woman’s rear end dressed only in lacy red underwear ... ....
« back to news headlines
Southern Nigerian oil facilities hit in militant attack
Edit Modern Ghana 07 Jul 2016
By AFP ... By Dave Clark (AFP/File) ... The group said in an email that it hit manifolds RMP 22, 23 and 24 operated by Chevron Nigeria Limited in Delta state at about 1.20 am (0020 GMT) ... RMPs or remote manifold platforms are where smaller oil and gas pipelines converge before being sent to larger lines ... ....
Nigeria Rebels Strike Chevron, Putting Output Recovery in Doubt
Edit Bloomberg 07 Jul 2016
Nigerian militants claimed an attack on oil pipelines less than two weeks after the government declared a cease-fire, while a worker strike further hampered efforts to restore production in the West African country. Rebels late on Wednesday blew up remote manifolds, or pipe systems, operated by Chevron Corp., according to a website claiming to represent the Niger Delta Avengers group ... “Our strike team blew up Chevron manifolds.” ... ....
BRIEF-Niger Delta Avengers says "between the hours of 1050 pm to 1110 pm, strike team ...
Edit Reuters 07 Jul 2016
* Niger Delta Avengers militant group says "between the hours of 10.50 pm to 11.10 pm, strike team blew up Chevron manifolds" ....
Physics and Mathematics Professors Named Simons Investigators (California Institute of Technology)
Edit Public Technologies 07 Jul 2016
(Source. California Institute of Technology). Anton Kapustin (PhD '97), the Earle C. Anthony Professor of Theoretical Physics and Mathematics, and Vladimir Markovic, the John D. MacArthur Professor of Mathematics, have been named Simons Investigators ... 'The main themes of my research are manifolds-a particular kind of topological space-and more generally groups, and their geometric, topological and dynamical properties,' says Markovic....
Zee deploys NexGuard forensic watermarking to curb online piracy
Edit DNA India 07 Jul 2016
-->. India's leading entertainment company Zee Entertainment Enterprises Ltd (Zeel) is deploying its NexGuard forensic watermarking system at its Mumbai facilities. The move, according to Zee management, is a major step towards dealing with online piracy of content ... This enhances our content security manifold, and above all, it acts as a powerful deterrent against piracy," said Buch ... dna Correspondent. ....
Erweiterung des Polyamid-Portfolios für die Ladeluftstrecke in modernen Verbrennungsmotoren (BASF SE)
Edit Public Technologies 07 Jul 2016
(Source. BASF SE) Ultramid grades for various demands on pressure and resistance up to 220°C Selected polyamides available with globally consistent specifications, locally manufactured ... Due to its excellent burst pressure and weld strength, it is suitable for air intake manifolds made from several parts ... They are proven to work well in air intake manifolds of turbocharged diesel engines as well as in resonators and sensors ... About BASF....
Tailored polyamide portfolio for the charge-air duct in modern combustion engines (BASF SE)
Edit Public Technologies 07 Jul 2016
(Source. BASF SE) Ultramid grades for various demands on pressure and resistance up to 220°C Selected polyamides available with globally consistent specifications, locally manufactured ... Due to its excellent burst pressure and weld strength, it is suitable for air intake manifolds made from several parts ... They are proven to work well in air intake manifolds of turbocharged diesel engines as well as in resonators and sensors ... About BASF....
Oil Rises a Second Day as U.S. Crude Stockpiles Seen Declining
Edit Bloomberg 07 Jul 2016
Oil extended gains as U.S. industry data showed the nation’s crude stockpiles fell last week, easing a surplus in the world’s biggest crude consumer. Futures rose as much as 1.5 percent in New York ... In Nigeria, further attacks on oil installations make it increasingly unlikely that production will return to normal, Commerzbank AG said ... Although the recovery has prompted U.S ... “Improving fundamentals, most notably declining U.S ... manifolds ... ....
National Oilwell Varco and GE Oil & Gas Cooperate to Provide Integrated Solutions for Floating Production Storage and Offloading (FPSO) Vessels (National Oilwell Varco Inc)
Edit Public Technologies 07 Jul 2016
(Source. National Oilwell Varco Inc) http.//www.businesswire.com/news/home/20160707005434/en/ ... Additionally, NOV has successfully installed and commissioned equipment on hundreds of vessels in dozens of shipyards for the oil and gas drilling industry ... Also, with its Subsea Production Systems, GE Oil & Gas offers a comprehensive range of solutions including subsea trees, manifold & connection systems, and power & processing technology ... T....
National Oilwell Varco and GE Oil & Gas cooperate to provide integrated solutions for Floating Production Storage and Offloading (FPSO) vessels (GE - General Electric Company)
Edit Public Technologies 07 Jul 2016
(Source. GE - General Electric Company). London, 7 July 2016 - National Oilwell Varco, Inc. (NYSE ... Additionally, NOV has successfully installed and commissioned equipment on hundreds of vessels in dozens of shipyards for the oil and gas drilling industry ... Also, with its Subsea Production Systems, GE Oil & Gas offers a comprehensive range of solutions including subsea trees, manifold & connection systems, and power & processing technology....
National Oilwell Varco and GE Oil & Gas Cooperate to Provide Integrated Solutions for Floating ...
Edit Stockhouse 07 Jul 2016
National Oilwell Varco, Inc. (NYSE. NOV) and GE Oil & Gas announced today the execution of an agreement to collaborate on delivering integrated solutions for Floating Production Storage and Offloading (FPSO) vessels ... Also, with its Subsea Production Systems, GE Oil & Gas offers a comprehensive range of solutions including subsea trees, manifold & connection systems, and power & processing technology ... -ends- ... 713-346-7807....
Research and Markets - Global Valves & Manifolds Market CAGR Growth of 6.56% by 2020 ...
Edit PR Newswire 06 Jul 2016
DUBLIN, July 6, 2016 /PRNewswire/ -- Research and Markets has announced the addition of the "Global Valves and Manifolds Market 2016-2020" report to their offering. The report forecasts the global valves and manifolds market to grow at a CAGR of 6.56% during the period 2016-2020 ... ....
- 1
- 2
- 3
- 4
- 5
- Next page »
