- published: 21 Jan 2008
- views: 65719
Create your page here
-
remove the playlistParallel (geometry)
-
remove the playlistLatest Videos
-
remove the playlistLongest Videos
- remove the playlistParallel (geometry)
- remove the playlistLatest Videos
- remove the playlistLongest Videos
back to playlist
MathHelp.com offers comprehensive geometry help with a personal math teacher. In this sample video, students learn that, if two parallel lines are cut by a transversal, then corresponding angles are congruent, alternate interior angles are congruent, and same-side interior angles are supplementary. Do you need geometry help? Visit us today at http://www.mathhelp.com/geometry-help.php
Do the two lines intersect or stay apart? If they intersect, do they do so thereby creating a 90 degree angle? These are the kinds of questions we ask ourselves when we learn about parallel and perpendicular lines.
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/equations-of-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/cc-distances-between-points/v/finding-a-point-part-way-between-two-points?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 17 Jul 2015
- views: 111135
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relationships of parallel lines: corresponding, alternate interior, alternate exterior, same-side interior, and same-side exterior. Some books call them "consecutive," but I like "same-side" because it's more obvious what that means. Oh, and I'm dressed as a security guard, green flashlight and all :-). YAY MATH!
Please visit yaymath.org
Videos copyright (c) Yay Math
- published: 26 Feb 2013
- views: 48724
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relationships of parallel lines: corresponding, alternate interior, alternate exterior angles, same-side interior, and same-side exterior. Oh, and I'm dressed as a security guard, green flashlight and all :-). YAY MATH!
Please visit yaymath.org
Videos copyright (c) Yay Math
- published: 30 Oct 2009
- views: 33946
Parallel lines, transversal lines, corresponding angles
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/identifying-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/proof-vertical-angles-are-equal?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 21 Sep 2011
- views: 399571
Angles of parallel lines
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-of-parallel-lines-2?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-part-3?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 09 Aug 2010
- views: 148707
Let's now apply what we learned and do an exercise together in which we identify parallel and perpendicular lines.This is great practice.
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/figuring-out-angles-between-transversal-and-parallel-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/angles-formed-by-parallel-lines-and-transversals?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 10 Nov 2011
- views: 196765
All videos can be found at www.m4ths.com and www.astarmaths.com
These videos were donated to the channel by Steve Blades of maths247 'fame'. Please share via twitter or facebook if you find them helpful.
Designed for the Edexcel spec but applicable to AQA, OCR,MEI and WJEC.
- published: 15 Mar 2014
- views: 11601
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/using-algebra-to-find-measures-of-angles-formed-from-transversal?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/identifying-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 07 Aug 2013
- views: 153930
Proof by contradiction that corresponding angle equivalence implies parallel lines
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/triang_prop_tut/v/finding-more-angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/triang_prop_tut/v/challenging-triangle-angle-problem?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 22 Sep 2011
- views: 100407
Equations of Parallel and Perpendicular Lines
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/distance-between-a-point-and-a-line?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/parallel-and-perpendicular-lines-intro?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 06 Apr 2010
- views: 409438
Parallelism is a term in geometry that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not intersect or touch at a point are called parallel lines. Likewise, a line and a plane, or two planes, in three-dimensional Euclidean space that do not share a point are said to be parallel.
In a non-Euclidean space, parallel lines are those that intersect only in the limit at infinity.
The parallel symbol is Failed to parse (Missing texvc executable; please see math/README to configure.): \parallel
In the Unicode character set, the 'parallel' and 'not parallel' signs have codepoints U+2225 (∥) and U+2226 (∦) respectively.
Given straight lines l and m, the following descriptions of line m equivalently define it as parallel to line l in Euclidean space:
In other words, parallel lines must be located in the same plane, and parallel planes must be located in the same three-dimensional space. A parallel combination of a line and a plane may be located in the same three-dimensional space. Lines parallel to each other have the same gradient. Compare to perpendicular.
This page contains text from Wikipedia, the Free Encyclopedia -
http://en.wikipedia.org/wiki/Parallel_(geometry)
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
Parallel may refer to:
This page contains text from Wikipedia, the Free Encyclopedia -
http://en.wikipedia.org/wiki/Parallel
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
Geometry (Ancient Greek: γεωμετρία; geo- "earth", -metria "measurement") is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer. Geometry arose independently in a number of early cultures as a body of practical knowledge concerning lengths, areas, and volumes, with elements of a formal mathematical science emerging in the West as early as Thales (6th Century BC). By the 3rd century BC geometry was put into an axiomatic form by Euclid, whose treatment—Euclidean geometry—set a standard for many centuries to follow.Archimedes developed ingenious techniques for calculating areas and volumes, in many ways anticipating modern integral calculus. The field of astronomy, especially mapping the positions of the stars and planets on the celestial sphere and describing the relationship between movements of celestial bodies, served as an important source of geometric problems during the next one and a half millennia. Both geometry and astronomy were considered in the classical world to be part of the Quadrivium, a subset of the seven liberal arts considered essential for a free citizen to master.
This page contains text from Wikipedia, the Free Encyclopedia -
http://en.wikipedia.org/wiki/Geometry
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...
-
3:31Geometry Help from MathHelp.com - Parallel Lines
Geometry Help from MathHelp.com - Parallel LinesGeometry Help from MathHelp.com - Parallel Lines
MathHelp.com offers comprehensive geometry help with a personal math teacher. In this sample video, students learn that, if two parallel lines are cut by a transversal, then corresponding angles are congruent, alternate interior angles are congruent, and same-side interior angles are supplementary. Do you need geometry help? Visit us today at http://www.mathhelp.com/geometry-help.php -
2:08Parallel and perpendicular lines intro | Analytic geometry | Geometry | Khan Academy
Parallel and perpendicular lines intro | Analytic geometry | Geometry | Khan AcademyParallel and perpendicular lines intro | Analytic geometry | Geometry | Khan Academy
Do the two lines intersect or stay apart? If they intersect, do they do so thereby creating a 90 degree angle? These are the kinds of questions we ask ourselves when we learn about parallel and perpendicular lines. Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Watch the next lesson: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/equations-of-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/analytic-geometry-topic/cc-distances-between-points/v/finding-a-point-part-way-between-two-points?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry. About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content. For free. For everyone. Forever. #YouCanLearnAnything Subscribe to Khan Academy’s Geometry channel: https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1 Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy -
34:33Geometry - Parallel Lines and Transversals
Geometry - Parallel Lines and TransversalsGeometry - Parallel Lines and Transversals
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relationships of parallel lines: corresponding, alternate interior, alternate exterior, same-side interior, and same-side exterior. Some books call them "consecutive," but I like "same-side" because it's more obvious what that means. Oh, and I'm dressed as a security guard, green flashlight and all :-). YAY MATH! Please visit yaymath.org Videos copyright (c) Yay Math -
9:44Geometry - Parallel Lines and Transversals
Geometry - Parallel Lines and TransversalsGeometry - Parallel Lines and Transversals
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relationships of parallel lines: corresponding, alternate interior, alternate exterior angles, same-side interior, and same-side exterior. Oh, and I'm dressed as a security guard, green flashlight and all :-). YAY MATH! Please visit yaymath.org Videos copyright (c) Yay Math -
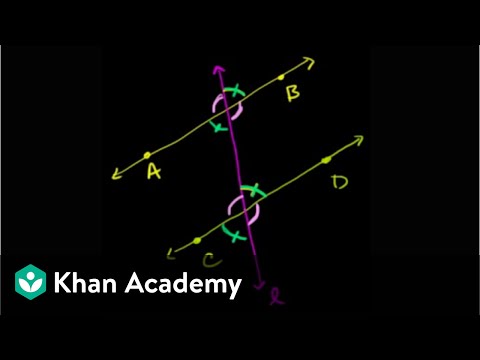7:08Angles formed by parallel lines and transversals | Geometry | Khan Academy
Angles formed by parallel lines and transversals | Geometry | Khan AcademyAngles formed by parallel lines and transversals | Geometry | Khan Academy
Parallel lines, transversal lines, corresponding angles Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/identifying-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/proof-vertical-angles-are-equal?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry. About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content. For free. For everyone. Forever. #YouCanLearnAnything Subscribe to Khan Academy’s Geometry channel: https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1 Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy -
7:53Angles formed between transversals and parallel lines | Geometry | Khan Academy
Angles formed between transversals and parallel lines | Geometry | Khan AcademyAngles formed between transversals and parallel lines | Geometry | Khan Academy
Angles of parallel lines Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-of-parallel-lines-2?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-part-3?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry. About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content. For free. For everyone. Forever. #YouCanLearnAnything Subscribe to Khan Academy’s Geometry channel: https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1 Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy -
3:35Identifying parallel and perpendicular lines | Geometry | Khan Academy
Identifying parallel and perpendicular lines | Geometry | Khan AcademyIdentifying parallel and perpendicular lines | Geometry | Khan Academy
Let's now apply what we learned and do an exercise together in which we identify parallel and perpendicular lines.This is great practice. Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/figuring-out-angles-between-transversal-and-parallel-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/angles-formed-by-parallel-lines-and-transversals?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry. About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content. For free. For everyone. Forever. #YouCanLearnAnything Subscribe to Khan Academy’s Geometry channel: https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1 Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy -
9:39Geometry: 3-2 Angles formed by Parallel Lines and Transversals
Geometry: 3-2 Angles formed by Parallel Lines and Transversals -
31:58GCSE Maths - Angles in Parallel Lines - Foundation Higher - Geometry - Linear Edexcel Revision
GCSE Maths - Angles in Parallel Lines - Foundation Higher - Geometry - Linear Edexcel RevisionGCSE Maths - Angles in Parallel Lines - Foundation Higher - Geometry - Linear Edexcel Revision
All videos can be found at www.m4ths.com and www.astarmaths.com These videos were donated to the channel by Steve Blades of maths247 'fame'. Please share via twitter or facebook if you find them helpful. Designed for the Edexcel spec but applicable to AQA, OCR,MEI and WJEC. -
2:16Figuring out angles between transversal and parallel lines | Geometry | Khan Academy
Figuring out angles between transversal and parallel lines | Geometry | Khan AcademyFiguring out angles between transversal and parallel lines | Geometry | Khan Academy
Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/using-algebra-to-find-measures-of-angles-formed-from-transversal?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/identifying-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry. About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content. For free. For everyone. Forever. #YouCanLearnAnything Subscribe to Khan Academy’s Geometry channel: https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1 Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy -
5:18Proof: Corresponding angle equivalence implies parallel lines | Geometry | Khan Academy
Proof: Corresponding angle equivalence implies parallel lines | Geometry | Khan AcademyProof: Corresponding angle equivalence implies parallel lines | Geometry | Khan Academy
Proof by contradiction that corresponding angle equivalence implies parallel lines Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/triang_prop_tut/v/finding-more-angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/triang_prop_tut/v/challenging-triangle-angle-problem?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry. About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content. For free. For everyone. Forever. #YouCanLearnAnything Subscribe to Khan Academy’s Geometry channel: https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1 Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy -
9:13Equations of parallel and perpendicular lines | Analytic geometry | Geometry | Khan Academy
Equations of parallel and perpendicular lines | Analytic geometry | Geometry | Khan AcademyEquations of parallel and perpendicular lines | Analytic geometry | Geometry | Khan Academy
Equations of Parallel and Perpendicular Lines Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Watch the next lesson: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/distance-between-a-point-and-a-line?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/parallel-and-perpendicular-lines-intro?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry. About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content. For free. For everyone. Forever. #YouCanLearnAnything Subscribe to Khan Academy’s Geometry channel: https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1 Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- Angle of parallelism
- Clifford parallel
- Coincident
- Curvature
- Dimension
- Elliptic geometry
- Equidistant
- Euclid
- Euclidean space
- Geodesic
- Geometry
- Great circle
- Great circles
- Hyperbolic geometry
- Infinity
- Latitude
- Limiting parallel
- Line (mathematics)
- Parallel (geometry)
- Parallel postulate
- Perpendicular
- Plane (mathematics)
- Sphere
- Spherical geometry
- Spherical plane
- Unicode
-
Geometry Help from MathHelp.com - Parallel Lines
MathHelp.com offers comprehensive geometry help with a personal math teacher. In this sample video, students learn that, if two parallel lines are cut by a transversal, then corresponding angles are congruent, alternate interior angles are congruent, and same-side interior angles are supplementary. Do you need geometry help? Visit us today at http://www.mathhelp.com/geometry-help.php -
Parallel and perpendicular lines intro | Analytic geometry | Geometry | Khan Academy
Do the two lines intersect or stay apart? If they intersect, do they do so thereby creating a 90 degree angle? These are the kinds of questions we ask ourselves when we learn about parallel and perpendicular lines. Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Watch the next lesson: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/equations-of-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/analytic-geometry-topic/cc-distances-between-points/v/finding-a-poin... -
Geometry - Parallel Lines and Transversals
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relationships of parallel lines: corresponding, alternate interior, alternate exterior, same-side interior, and same-side exterior. Some books call them "consecutive," but I like "same-side" because it's more obvious what that means. Oh, and I'm dressed as a security guard, green flashlight and all :-). YAY MATH! Please visit yaymath.org Videos copyright (c) Yay Math -
Geometry - Parallel Lines and Transversals
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relationships of parallel lines: corresponding, alternate interior, alternate exterior angles, same-side interior, and same-side exterior. Oh, and I'm dressed as a security guard, green flashlight and all :-). YAY MATH! Please visit yaymath.org Videos copyright (c) Yay Math -
Angles formed by parallel lines and transversals | Geometry | Khan Academy
Parallel lines, transversal lines, corresponding angles Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/identifying-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/proof-vertical-angles-are-equal?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have ... -
Angles formed between transversals and parallel lines | Geometry | Khan Academy
Angles of parallel lines Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-of-parallel-lines-2?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-part-3?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("... -
Identifying parallel and perpendicular lines | Geometry | Khan Academy
Let's now apply what we learned and do an exercise together in which we identify parallel and perpendicular lines.This is great practice. Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/figuring-out-angles-between-transversal-and-parallel-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/angles-formed-by-parallel-lines-and-transversals?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geo... -
-
GCSE Maths - Angles in Parallel Lines - Foundation Higher - Geometry - Linear Edexcel Revision
All videos can be found at www.m4ths.com and www.astarmaths.com These videos were donated to the channel by Steve Blades of maths247 'fame'. Please share via twitter or facebook if you find them helpful. Designed for the Edexcel spec but applicable to AQA, OCR,MEI and WJEC. -
Figuring out angles between transversal and parallel lines | Geometry | Khan Academy
Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/using-algebra-to-find-measures-of-angles-formed-from-transversal?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/identifying-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we a... -
Proof: Corresponding angle equivalence implies parallel lines | Geometry | Khan Academy
Proof by contradiction that corresponding angle equivalence implies parallel lines Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/triang_prop_tut/v/finding-more-angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/triang_prop_tut/v/challenging-triangle-angle-problem?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everyth... -
Equations of parallel and perpendicular lines | Analytic geometry | Geometry | Khan Academy
Equations of Parallel and Perpendicular Lines Practice this lesson yourself on KhanAcademy.org right now: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Watch the next lesson: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/distance-between-a-point-and-a-line?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/parallel-and-perpendicular-lines-intro?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And thes...
Geometry Help from MathHelp.com - Parallel Lines
- Order: Reorder
- Duration: 3:31
- Updated: 21 Jan 2008
- views: 65719
MathHelp.com offers comprehensive geometry help with a personal math teacher. In this sample video, students learn that, if two parallel lines are cut by a tra...
MathHelp.com offers comprehensive geometry help with a personal math teacher. In this sample video, students learn that, if two parallel lines are cut by a transversal, then corresponding angles are congruent, alternate interior angles are congruent, and same-side interior angles are supplementary. Do you need geometry help? Visit us today at http://www.mathhelp.com/geometry-help.php
wn.com/Geometry Help From Mathhelp.Com Parallel Lines
MathHelp.com offers comprehensive geometry help with a personal math teacher. In this sample video, students learn that, if two parallel lines are cut by a transversal, then corresponding angles are congruent, alternate interior angles are congruent, and same-side interior angles are supplementary. Do you need geometry help? Visit us today at http://www.mathhelp.com/geometry-help.php
- published: 21 Jan 2008
- views: 65719
Parallel and perpendicular lines intro | Analytic geometry | Geometry | Khan Academy
- Order: Reorder
- Duration: 2:08
- Updated: 17 Jul 2015
- views: 111135
Do the two lines intersect or stay apart? If they intersect, do they do so thereby creating a 90 degree angle? These are the kinds of questions we ask ourselves...
Do the two lines intersect or stay apart? If they intersect, do they do so thereby creating a 90 degree angle? These are the kinds of questions we ask ourselves when we learn about parallel and perpendicular lines.
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/equations-of-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/cc-distances-between-points/v/finding-a-point-part-way-between-two-points?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
wn.com/Parallel And Perpendicular Lines Intro | Analytic Geometry | Geometry | Khan Academy
Do the two lines intersect or stay apart? If they intersect, do they do so thereby creating a 90 degree angle? These are the kinds of questions we ask ourselves when we learn about parallel and perpendicular lines.
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/equations-of-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/cc-distances-between-points/v/finding-a-point-part-way-between-two-points?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 17 Jul 2015
- views: 111135
Geometry - Parallel Lines and Transversals
- Order: Reorder
- Duration: 34:33
- Updated: 26 Feb 2013
- views: 48724
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relations...
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relationships of parallel lines: corresponding, alternate interior, alternate exterior, same-side interior, and same-side exterior. Some books call them "consecutive," but I like "same-side" because it's more obvious what that means. Oh, and I'm dressed as a security guard, green flashlight and all :-). YAY MATH!
Please visit yaymath.org
Videos copyright (c) Yay Math
wn.com/Geometry Parallel Lines And Transversals
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relationships of parallel lines: corresponding, alternate interior, alternate exterior, same-side interior, and same-side exterior. Some books call them "consecutive," but I like "same-side" because it's more obvious what that means. Oh, and I'm dressed as a security guard, green flashlight and all :-). YAY MATH!
Please visit yaymath.org
Videos copyright (c) Yay Math
- published: 26 Feb 2013
- views: 48724
Geometry - Parallel Lines and Transversals
- Order: Reorder
- Duration: 9:44
- Updated: 30 Oct 2009
- views: 33946
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relations...
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relationships of parallel lines: corresponding, alternate interior, alternate exterior angles, same-side interior, and same-side exterior. Oh, and I'm dressed as a security guard, green flashlight and all :-). YAY MATH!
Please visit yaymath.org
Videos copyright (c) Yay Math
wn.com/Geometry Parallel Lines And Transversals
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in this introductory lesson that discusses the five main angle relationships of parallel lines: corresponding, alternate interior, alternate exterior angles, same-side interior, and same-side exterior. Oh, and I'm dressed as a security guard, green flashlight and all :-). YAY MATH!
Please visit yaymath.org
Videos copyright (c) Yay Math
- published: 30 Oct 2009
- views: 33946
Angles formed by parallel lines and transversals | Geometry | Khan Academy
- Order: Reorder
- Duration: 7:08
- Updated: 21 Sep 2011
- views: 399571
Parallel lines, transversal lines, corresponding angles
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/...
Parallel lines, transversal lines, corresponding angles
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/identifying-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/proof-vertical-angles-are-equal?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
wn.com/Angles Formed By Parallel Lines And Transversals | Geometry | Khan Academy
Parallel lines, transversal lines, corresponding angles
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/identifying-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/proof-vertical-angles-are-equal?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 21 Sep 2011
- views: 399571
Angles formed between transversals and parallel lines | Geometry | Khan Academy
- Order: Reorder
- Duration: 7:53
- Updated: 09 Aug 2010
- views: 148707
Angles of parallel lines
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-of-parallel-line...
Angles of parallel lines
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-of-parallel-lines-2?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-part-3?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
wn.com/Angles Formed Between Transversals And Parallel Lines | Geometry | Khan Academy
Angles of parallel lines
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-of-parallel-lines-2?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/old_angles/v/angles-part-3?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 09 Aug 2010
- views: 148707
Identifying parallel and perpendicular lines | Geometry | Khan Academy
- Order: Reorder
- Duration: 3:35
- Updated: 10 Nov 2011
- views: 196765
Let's now apply what we learned and do an exercise together in which we identify parallel and perpendicular lines.This is great practice.
Practice this lesson ...
Let's now apply what we learned and do an exercise together in which we identify parallel and perpendicular lines.This is great practice.
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/figuring-out-angles-between-transversal-and-parallel-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/angles-formed-by-parallel-lines-and-transversals?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
wn.com/Identifying Parallel And Perpendicular Lines | Geometry | Khan Academy
Let's now apply what we learned and do an exercise together in which we identify parallel and perpendicular lines.This is great practice.
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/figuring-out-angles-between-transversal-and-parallel-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/angles-formed-by-parallel-lines-and-transversals?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 10 Nov 2011
- views: 196765
Geometry: 3-2 Angles formed by Parallel Lines and Transversals
- Order: Reorder
- Duration: 9:39
- Updated: 31 Jul 2010
- views: 42006
If these helped at all, PRETTY PLEASE Like my Facebook Page: http://facebook.com/tylersokay
http://tylertarver.com Prove and use theorems about the angles form...
If these helped at all, PRETTY PLEASE Like my Facebook Page: http://facebook.com/tylersokay
http://tylertarver.com Prove and use theorems about the angles formed by parallel lines and a transversal. Drop the would on your head....
wn.com/Geometry 3 2 Angles Formed By Parallel Lines And Transversals
GCSE Maths - Angles in Parallel Lines - Foundation Higher - Geometry - Linear Edexcel Revision
- Order: Reorder
- Duration: 31:58
- Updated: 15 Mar 2014
- views: 11601
All videos can be found at www.m4ths.com and www.astarmaths.com
These videos were donated to the channel by Steve Blades of maths247 'fame'. Please share via tw...
All videos can be found at www.m4ths.com and www.astarmaths.com
These videos were donated to the channel by Steve Blades of maths247 'fame'. Please share via twitter or facebook if you find them helpful.
Designed for the Edexcel spec but applicable to AQA, OCR,MEI and WJEC.
wn.com/Gcse Maths Angles In Parallel Lines Foundation Higher Geometry Linear Edexcel Revision
All videos can be found at www.m4ths.com and www.astarmaths.com
These videos were donated to the channel by Steve Blades of maths247 'fame'. Please share via twitter or facebook if you find them helpful.
Designed for the Edexcel spec but applicable to AQA, OCR,MEI and WJEC.
- published: 15 Mar 2014
- views: 11601
Figuring out angles between transversal and parallel lines | Geometry | Khan Academy
- Order: Reorder
- Duration: 2:16
- Updated: 07 Aug 2013
- views: 153930
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_an...
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/using-algebra-to-find-measures-of-angles-formed-from-transversal?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/identifying-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
wn.com/Figuring Out Angles Between Transversal And Parallel Lines | Geometry | Khan Academy
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/e/congruent_angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/using-algebra-to-find-measures-of-angles-formed-from-transversal?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/ang_intro/v/identifying-parallel-and-perpendicular-lines?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 07 Aug 2013
- views: 153930
Proof: Corresponding angle equivalence implies parallel lines | Geometry | Khan Academy
- Order: Reorder
- Duration: 5:18
- Updated: 22 Sep 2011
- views: 100407
Proof by contradiction that corresponding angle equivalence implies parallel lines
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-an...
Proof by contradiction that corresponding angle equivalence implies parallel lines
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/triang_prop_tut/v/finding-more-angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/triang_prop_tut/v/challenging-triangle-angle-problem?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
wn.com/Proof Corresponding Angle Equivalence Implies Parallel Lines | Geometry | Khan Academy
Proof by contradiction that corresponding angle equivalence implies parallel lines
Watch the next lesson: https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/triang_prop_tut/v/finding-more-angles?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/parallel-and-perpendicular-lines/triang_prop_tut/v/challenging-triangle-angle-problem?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 22 Sep 2011
- views: 100407
Equations of parallel and perpendicular lines | Analytic geometry | Geometry | Khan Academy
- Order: Reorder
- Duration: 9:13
- Updated: 06 Apr 2010
- views: 409438
Equations of Parallel and Perpendicular Lines
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/analytic-g...
Equations of Parallel and Perpendicular Lines
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/distance-between-a-point-and-a-line?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/parallel-and-perpendicular-lines-intro?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
wn.com/Equations Of Parallel And Perpendicular Lines | Analytic Geometry | Geometry | Khan Academy
Equations of Parallel and Perpendicular Lines
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Watch the next lesson: https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/distance-between-a-point-and-a-line?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Missed the previous lesson?
https://www.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/v/parallel-and-perpendicular-lines-intro?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry
Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything in between). Learning geometry is about more than just taking your medicine ("It's good for you!"), it's at the core of everything that exists--including you. Having said all that, some of the specific topics we'll cover include angles, intersecting lines, right triangles, perimeter, area, volume, circles, triangles, quadrilaterals, analytic geometry, and geometric constructions. Wow. That's a lot. To summarize: it's difficult to imagine any area of math that is more widely used than geometry.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to Khan Academy’s Geometry channel:
https://www.youtube.com/channel/UCD3OtKxPRUFw8kzYlhJXa1Q?sub_confirmation=1
Subscribe to Khan Academy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 06 Apr 2010
- views: 409438
-
Geometry - Parallel Lines and Transversals; Angle Relationships SOL Review
-
How to draw a parallel through any point using a compass
Constructing a parallel through a point. This YouTube channel is dedicated to teaching people how to improve their technical drawing skills. It focusses on drawing figures from the geometric plane to descriptive geometry and also different systems of technical drawing representation. If you subscribe, click, like or leave a comment you will be helping us to grow our channel and help more people with their technical drawing skills. Thank you in advance. -
Geometry final. Geometry in the real world 2016
Geometry final. Geometry in the real world. parallel lines in the main gym on the floor perpendicular lines in the main gym on the floor triangles: Right triangle is in the four in 2014 in the hallway Isosceles is a flag that was in Mrs. water's room obtuse triangle: a flag that was in a case in the commons Quadrilaterals: Kite: was an actual kite that is in Mrs. Driskill's room Rectangle: the box holding the fire extinguisher in the 300 hallway square was a school plaque in the commons -
Download [PDF] Vectors and Coordinate Geometry
detail http://book99download.com/readbook.php?asin=1523688661.html Vectors and Coordinate Geometry Coordinate Geometry - Online Math Learning Coordinate Geometry coordinate geometry problems Coordinate plane Slope Formula Equation of a Line Slopes of parallel lines Slope of perpendicular lines ... Practice Geometry Brilliant 3D Coordinate Geometry - Equation of a Line 3D Coordinate Geometry - Skew Lines 3D Coordinate Geometry - Equation of a Plane 3D Coordinate Geometry - Parallel Planes 3D Coordinate Geometry - Perpendicular Planes Adding Vectors Algebraically - Khan Academy Learn for free about math art computer programming economics physics chemistry biology medicine finance history and more. Khan Academy is a nonprofit with ... Euclidean space - Wikipedia the free encyclopedia In geome... -
Vectors and Coordinate Geometry
detail link :: http://book99download.com/readbook.php?asin=1523688661.html Vectors and Coordinate Geometry Coordinate Systems Points Lines and Planes Coordinate Systems Points Lines and Planes Two-Dimensional Objects Points The xy-coordinate plane has two coordinate axes the x- and y-axis. Coordinate Geometry - Online Math Learning Coordinate Geometry coordinate geometry problems Coordinate plane Slope Formula Equation of a Line Slopes of parallel lines Slope of perpendicular lines ... Physics -- Unit vectors along coordinate axis - YouTube Sri RAGHU Kalidindi a renowned academician with more than 25 years of experience in teaching and running Educational Institutions has developed content for ... Vector their Magnitude & Direction. Defined with Examples ... Vector magnitude and direction ... -
-
Geometry dash - [2.0] - [Demon] - Parallel Run By Dhafin - TheJaco9
Demon difficultly: 2/10★ (Very easy demon) ---------------------------------------------------------------------------------------------------- ID: 5439175 ---------------------------------------------------------------------------------------------------- Like en facebook! https://www.facebook.com/JJSMTJ9/?fre... Sígueme en twitter! https://twitter.com/TheJaco9 -
-
Geometry Dash 2.1 VS 2.0? : All Sneak Peek + All Fan Made (Parallel)
♬ Geometry Dash 2.1 VS 2.0 (?) Fan Made And Real Sneak Peek (FireBall + FingerBang + Spider Mode (Do That With The Ball) Sub And Like Plz~ Some Suck Sync.. Sorry Cause It.s not matched some.. sorry But I Tried Best :3 Level Support : Robtop / Dudex / DestructorGD / N4XOL ♬ Partition More Video List ◆ Random Story? In Geometry Dash : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqPVpZRBKGG6emqQy5Gq4fb ◆ Geometry Dash Song / Bgm FULL TIME LEVEL : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqpZC0--vswOUr7E9qGVfeO ◆ Geometry Dash Mad Movie : https://www.youtube.com/playlist?list=PLxLTiR9IMRqrygjhMOLw8N1_9y-0LKH7L ◆ Geometry Dash Series Level / Top 5~10 : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqD8RbCorTZZtIpjmbbDdQW ◆ Geometry Dash Rhythm Game Cover (My Special? ... -
Maths By Amiya Geometry 3 Similarity 1 Parallel Lines in Triangle
Application of Parallel lines in triangle If in ∆ ABC , points D, F & H are on side AB & E, G & I are on side AC BC || DE || FG || HI and AH=HF=FD=DB then what is the area ratio of ∎DEIH to that of ∎BCGF -
Geometry Dash (Very Easy Demon) - Parallel World - by lRabb2tl
lel this level made me remember too much stuff. Level ID: 79939 https://everyplay.com/videos/28178158 Video recorded with Everyplay. Download Geometry Dash on the App Store: https://itunes.apple.com/app/id625334537 -
Paced Geometry (2.3) - Proving Lines Parallel (Part 1 of 2)
Greetings Everyone, totonbutton here on study mode. In approximately 1 month from this moment will be my EOC for Geometry, and I wanted to prepare, by making youtube videos because I love talking. Hope you find it even a bit helpful. =================================================== Youtube Channel: https://www.youtube.com/user/ecityzen2 Google+ Account: https://plus.google.com/u/0/b/117019035866834037340/117019035866834037340/posts?pageId=117019035866834037340 I don't have any other Social Media accounts, if you see my account on facebook or twitter or snapchat or instagram or any other social media except the one's viewed here in the description are not me unless I warn you guys. This is a warning to all fakers out there. Thank you and Goodbye, enjoy the video and have a nice life.
Geometry - Parallel Lines and Transversals; Angle Relationships SOL Review
- Order: Reorder
- Duration: 15:01
- Updated: 12 May 2016
- views: 1
- published: 12 May 2016
- views: 1
How to draw a parallel through any point using a compass
- Order: Reorder
- Duration: 2:01
- Updated: 12 May 2016
- views: 16
Constructing a parallel through a point.
This YouTube channel is dedicated to teaching people how to improve their technical drawing skills. It focusses on dra...
Constructing a parallel through a point.
This YouTube channel is dedicated to teaching people how to improve their technical drawing skills. It focusses on drawing figures from the geometric plane to descriptive geometry and also different systems of technical drawing representation.
If you subscribe, click, like or leave a comment you will be helping us to grow our channel and help more people with their technical drawing skills.
Thank you in advance.
wn.com/How To Draw A Parallel Through Any Point Using A Compass
Constructing a parallel through a point.
This YouTube channel is dedicated to teaching people how to improve their technical drawing skills. It focusses on drawing figures from the geometric plane to descriptive geometry and also different systems of technical drawing representation.
If you subscribe, click, like or leave a comment you will be helping us to grow our channel and help more people with their technical drawing skills.
Thank you in advance.
- published: 12 May 2016
- views: 16
Geometry final. Geometry in the real world 2016
- Order: Reorder
- Duration: 1:45
- Updated: 09 May 2016
- views: 13
Geometry final. Geometry in the real world.
parallel lines in the main gym on the floor
perpendicular lines in the main gym on the floor
triangles:
Right tria...
Geometry final. Geometry in the real world.
parallel lines in the main gym on the floor
perpendicular lines in the main gym on the floor
triangles:
Right triangle is in the four in 2014 in the hallway
Isosceles is a flag that was in Mrs. water's room
obtuse triangle: a flag that was in a case in the commons
Quadrilaterals:
Kite: was an actual kite that is in Mrs. Driskill's room
Rectangle: the box holding the fire extinguisher in the 300 hallway
square was a school plaque in the commons
wn.com/Geometry Final. Geometry In The Real World 2016
Geometry final. Geometry in the real world.
parallel lines in the main gym on the floor
perpendicular lines in the main gym on the floor
triangles:
Right triangle is in the four in 2014 in the hallway
Isosceles is a flag that was in Mrs. water's room
obtuse triangle: a flag that was in a case in the commons
Quadrilaterals:
Kite: was an actual kite that is in Mrs. Driskill's room
Rectangle: the box holding the fire extinguisher in the 300 hallway
square was a school plaque in the commons
- published: 09 May 2016
- views: 13
Download [PDF] Vectors and Coordinate Geometry
- Order: Reorder
- Duration: 0:16
- Updated: 08 May 2016
- views: 0
detail http://book99download.com/readbook.php?asin=1523688661.html Vectors and Coordinate Geometry Coordinate Geometry - Online Math Learning Coordinate Geometr...
detail http://book99download.com/readbook.php?asin=1523688661.html Vectors and Coordinate Geometry Coordinate Geometry - Online Math Learning Coordinate Geometry coordinate geometry problems Coordinate plane Slope Formula Equation of a Line Slopes of parallel lines Slope of perpendicular lines ... Practice Geometry Brilliant 3D Coordinate Geometry - Equation of a Line 3D Coordinate Geometry - Skew Lines 3D Coordinate Geometry - Equation of a Plane 3D Coordinate Geometry - Parallel Planes 3D Coordinate Geometry - Perpendicular Planes Adding Vectors Algebraically - Khan Academy Learn for free about math art computer programming economics physics chemistry biology medicine finance history and more. Khan Academy is a nonprofit with ... Euclidean space - Wikipedia the free encyclopedia In geometry Euclidean space encompasses the two-dimensional Euclidean plane the three-dimensional space of Euclidean geometry and certain other spaces. It is named ... Euclidean vector - Wikipedia the free encyclopedia In order to calculate with vectors the graphical representation may be too cumbersome. Vectors in an n-dimensional Euclidean space can be represented as coordinate ... Vector their Magnitude & Direction. Defined with Examples ... Vector magnitude and direction of vector defined with examples and practice problems. ... A Vector is something that has two and only two defining characteristics. ... The significance of 'direction' can be seen in the difference between velocity and speed. I. Vectors and Geometry in Two and Three Dimensions I. Vectors and Geometry in Two and Three Dimensions I.1 Pointsand Vectors Each point in two dimensions may be labeled by two coordinates (ab) which specify the ... Application of coordinate system and vectors in the real life Application of coordinate system and vectors in the real life 1. Application of coordinate systems and vectors in the real life likbr Rhimli lkin Vectors and Plane Geometry Vectors and Plane Geometry Karl Heinz Dovermann Professor of Mathematics University of Hawaii ... Preface During the rst week of the semester it is dicult to ... Physics -- Unit vectors along coordinate axis - YouTube Sri RAGHU Kalidindi a renowned academician with more than 25 years of experience in teaching and running Educational Institutions has developed content for ... Published on: 2016-02-24 Original language: English Number of items: 1 Dimensions: 10.00" h x .44" w x 8.00" l, 1.15 pounds Binding: Paperback 184 pages
wn.com/Download Pdf Vectors And Coordinate Geometry
detail http://book99download.com/readbook.php?asin=1523688661.html Vectors and Coordinate Geometry Coordinate Geometry - Online Math Learning Coordinate Geometry coordinate geometry problems Coordinate plane Slope Formula Equation of a Line Slopes of parallel lines Slope of perpendicular lines ... Practice Geometry Brilliant 3D Coordinate Geometry - Equation of a Line 3D Coordinate Geometry - Skew Lines 3D Coordinate Geometry - Equation of a Plane 3D Coordinate Geometry - Parallel Planes 3D Coordinate Geometry - Perpendicular Planes Adding Vectors Algebraically - Khan Academy Learn for free about math art computer programming economics physics chemistry biology medicine finance history and more. Khan Academy is a nonprofit with ... Euclidean space - Wikipedia the free encyclopedia In geometry Euclidean space encompasses the two-dimensional Euclidean plane the three-dimensional space of Euclidean geometry and certain other spaces. It is named ... Euclidean vector - Wikipedia the free encyclopedia In order to calculate with vectors the graphical representation may be too cumbersome. Vectors in an n-dimensional Euclidean space can be represented as coordinate ... Vector their Magnitude & Direction. Defined with Examples ... Vector magnitude and direction of vector defined with examples and practice problems. ... A Vector is something that has two and only two defining characteristics. ... The significance of 'direction' can be seen in the difference between velocity and speed. I. Vectors and Geometry in Two and Three Dimensions I. Vectors and Geometry in Two and Three Dimensions I.1 Pointsand Vectors Each point in two dimensions may be labeled by two coordinates (ab) which specify the ... Application of coordinate system and vectors in the real life Application of coordinate system and vectors in the real life 1. Application of coordinate systems and vectors in the real life likbr Rhimli lkin Vectors and Plane Geometry Vectors and Plane Geometry Karl Heinz Dovermann Professor of Mathematics University of Hawaii ... Preface During the rst week of the semester it is dicult to ... Physics -- Unit vectors along coordinate axis - YouTube Sri RAGHU Kalidindi a renowned academician with more than 25 years of experience in teaching and running Educational Institutions has developed content for ... Published on: 2016-02-24 Original language: English Number of items: 1 Dimensions: 10.00" h x .44" w x 8.00" l, 1.15 pounds Binding: Paperback 184 pages
- published: 08 May 2016
- views: 0
Vectors and Coordinate Geometry
- Order: Reorder
- Duration: 0:16
- Updated: 06 May 2016
- views: 0
detail link :: http://book99download.com/readbook.php?asin=1523688661.html Vectors and Coordinate Geometry Coordinate Systems Points Lines and Planes Coordinate...
detail link :: http://book99download.com/readbook.php?asin=1523688661.html Vectors and Coordinate Geometry Coordinate Systems Points Lines and Planes Coordinate Systems Points Lines and Planes Two-Dimensional Objects Points The xy-coordinate plane has two coordinate axes the x- and y-axis. Coordinate Geometry - Online Math Learning Coordinate Geometry coordinate geometry problems Coordinate plane Slope Formula Equation of a Line Slopes of parallel lines Slope of perpendicular lines ... Physics -- Unit vectors along coordinate axis - YouTube Sri RAGHU Kalidindi a renowned academician with more than 25 years of experience in teaching and running Educational Institutions has developed content for ... Vector their Magnitude & Direction. Defined with Examples ... Vector magnitude and direction of vector defined with examples and practice problems. Vectors and Plane Geometry - University of Hawaii Vectors and Plane Geometry Karl Heinz Dovermann Professor of Mathematics University of Hawaii January 27 2011 Practice Geometry Brilliant 3D Coordinate Geometry - Equation of a Line 3D Coordinate Geometry - Skew Lines 3D Coordinate Geometry - Equation of a Plane 3D Coordinate Geometry - Parallel Planes I. Vectors and Geometry in Two and Three Dimensions I. Vectors and Geometry in Two and Three Dimensions I.1 Pointsand Vectors Each point in two dimensions may be labeled by two coordinates (ab) which specify the ... Application of coordinate system and vectors in the real life Application of coordinate system and vectors in the real life 1. Application of coordinate systems and vectors in the real life likbr Rhimli lkin ... Euclidean vector - Wikipedia the free encyclopedia On a two-dimensional diagram sometimes a vector perpendicular to the plane of the diagram is desired. These vectors are commonly shown as small circles. Euclidean space - Wikipedia the free encyclopedia In geometry Euclidean space encompasses the two-dimensional Euclidean plane the three-dimensional space of Euclidean geometry and certain other spaces. Published on: 2016-02-24 Original language: English Number of items: 1 Dimensions: 10.00" h x .44" w x 8.00" l 1.15 pounds Binding: Paperback 184 pages
wn.com/Vectors And Coordinate Geometry
detail link :: http://book99download.com/readbook.php?asin=1523688661.html Vectors and Coordinate Geometry Coordinate Systems Points Lines and Planes Coordinate Systems Points Lines and Planes Two-Dimensional Objects Points The xy-coordinate plane has two coordinate axes the x- and y-axis. Coordinate Geometry - Online Math Learning Coordinate Geometry coordinate geometry problems Coordinate plane Slope Formula Equation of a Line Slopes of parallel lines Slope of perpendicular lines ... Physics -- Unit vectors along coordinate axis - YouTube Sri RAGHU Kalidindi a renowned academician with more than 25 years of experience in teaching and running Educational Institutions has developed content for ... Vector their Magnitude & Direction. Defined with Examples ... Vector magnitude and direction of vector defined with examples and practice problems. Vectors and Plane Geometry - University of Hawaii Vectors and Plane Geometry Karl Heinz Dovermann Professor of Mathematics University of Hawaii January 27 2011 Practice Geometry Brilliant 3D Coordinate Geometry - Equation of a Line 3D Coordinate Geometry - Skew Lines 3D Coordinate Geometry - Equation of a Plane 3D Coordinate Geometry - Parallel Planes I. Vectors and Geometry in Two and Three Dimensions I. Vectors and Geometry in Two and Three Dimensions I.1 Pointsand Vectors Each point in two dimensions may be labeled by two coordinates (ab) which specify the ... Application of coordinate system and vectors in the real life Application of coordinate system and vectors in the real life 1. Application of coordinate systems and vectors in the real life likbr Rhimli lkin ... Euclidean vector - Wikipedia the free encyclopedia On a two-dimensional diagram sometimes a vector perpendicular to the plane of the diagram is desired. These vectors are commonly shown as small circles. Euclidean space - Wikipedia the free encyclopedia In geometry Euclidean space encompasses the two-dimensional Euclidean plane the three-dimensional space of Euclidean geometry and certain other spaces. Published on: 2016-02-24 Original language: English Number of items: 1 Dimensions: 10.00" h x .44" w x 8.00" l 1.15 pounds Binding: Paperback 184 pages
- published: 06 May 2016
- views: 0
Geometry SOL Review RC1 Part 2: Proving Lines Parallel
- Order: Reorder
- Duration: 23:58
- Updated: 02 May 2016
- views: 79
Geometry 2015-16 SOL Review
Reporting Category 1: Reasoning, Lines, and Transformations
Part 2: Proving Lines Parallel
Geometry 2015-16 SOL Review
Reporting Category 1: Reasoning, Lines, and Transformations
Part 2: Proving Lines Parallel
wn.com/Geometry Sol Review Rc1 Part 2 Proving Lines Parallel
Geometry dash - [2.0] - [Demon] - Parallel Run By Dhafin - TheJaco9
- Order: Reorder
- Duration: 1:09
- Updated: 01 May 2016
- views: 6
Demon difficultly: 2/10★ (Very easy demon)
----------------------------------------------------------------------------------------------------
ID: 5439...
Demon difficultly: 2/10★ (Very easy demon)
----------------------------------------------------------------------------------------------------
ID: 5439175
----------------------------------------------------------------------------------------------------
Like en facebook! https://www.facebook.com/JJSMTJ9/?fre...
Sígueme en twitter! https://twitter.com/TheJaco9
wn.com/Geometry Dash 2.0 Demon Parallel Run By Dhafin Thejaco9
Demon difficultly: 2/10★ (Very easy demon)
----------------------------------------------------------------------------------------------------
ID: 5439175
----------------------------------------------------------------------------------------------------
Like en facebook! https://www.facebook.com/JJSMTJ9/?fre...
Sígueme en twitter! https://twitter.com/TheJaco9
- published: 01 May 2016
- views: 6
Geometry Dash - Parallel World (Very Easy Demon) by IRabb2tI
- Order: Reorder
- Duration: 1:43
- Updated: 22 Apr 2016
- views: 27
Geometry Dash 2.1 VS 2.0? : All Sneak Peek + All Fan Made (Parallel)
- Order: Reorder
- Duration: 1:34
- Updated: 20 Apr 2016
- views: 668
♬ Geometry Dash 2.1 VS 2.0 (?) Fan Made And Real Sneak Peek (FireBall + FingerBang + Spider Mode (Do That With The Ball)
Sub And Like Plz~
Some Suck Sync.. ...
♬ Geometry Dash 2.1 VS 2.0 (?) Fan Made And Real Sneak Peek (FireBall + FingerBang + Spider Mode (Do That With The Ball)
Sub And Like Plz~
Some Suck Sync.. Sorry
Cause It.s not matched some.. sorry But I Tried Best :3
Level Support : Robtop / Dudex / DestructorGD / N4XOL
♬ Partition More Video List
◆ Random Story? In Geometry Dash : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqPVpZRBKGG6emqQy5Gq4fb
◆ Geometry Dash Song / Bgm FULL TIME LEVEL : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqpZC0--vswOUr7E9qGVfeO
◆ Geometry Dash Mad Movie : https://www.youtube.com/playlist?list=PLxLTiR9IMRqrygjhMOLw8N1_9y-0LKH7L
◆ Geometry Dash Series Level / Top 5~10 : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqD8RbCorTZZtIpjmbbDdQW
◆ Geometry Dash Rhythm Game Cover (My Special? Work) : http://www.youtube.com/playlist?list=PLxLTiR9IMRqpWy-KJmELSSzWUubXny8yK
◆ Geometry Dash My Favorite Level / Cool Level : http://www.youtube.com/playlist?list=PLxLTiR9IMRqo7UEjh8aRvuig-jUjW2pkn
◆ My Demon Clear List : http://www.youtube.com/playlist?list=PLxLTiR9IMRqo_y_1QQZ-TkLDycZkYXhEh
◆ Geometry Dash My Creator Tutorial (How To Make~) : http://www.youtube.com/playlist?list=PLxLTiR9IMRqr44lnsCauQcICsPOjEBF6Z
◆ Geometry Dash Demon IF Series : http://www.youtube.com/playlist?list=PLxLTiR9IMRqrg2p5aNBw7v-WgtOUXw93z
◆ Geometry Dash Official Level Remix : http://www.youtube.com/playlist?list=PLxLTiR9IMRqpXUUDpjrzY9WsFWOe8ye3U
◆ Partition Geometry Dash Challenge : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqB-WFgKjXbCkGDVIBfr9eC
◆ Geometry Dash Official Level Robot Ver : http://www.youtube.com/playlist?list=PLxLTiR9IMRqp_3b974QRpAoTEZw51rh0j
◆ Geometry Dash 2.1 Info / Fan Made Level : http://www.youtube.com/playlist?list=PLxLTiR9IMRqo36r1uDxmsFPjEtfBsWMJ8
◆ Geometry Dash Secret Way / Free Star Level : http://www.youtube.com/playlist?list=PLxLTiR9IMRqq-sl5bwVZ3m4M0nmchfa4d
Geometry Dash / 지오메트리대쉬 / Partition / 파티션 / 시온 / Sion / ジオメトリダッシュ / 지오메트리대쉬 2.0 / 핑거뱅 / Geometry Dash FingerBang
wn.com/Geometry Dash 2.1 Vs 2.0 All Sneak Peek All Fan Made (Parallel)
♬ Geometry Dash 2.1 VS 2.0 (?) Fan Made And Real Sneak Peek (FireBall + FingerBang + Spider Mode (Do That With The Ball)
Sub And Like Plz~
Some Suck Sync.. Sorry
Cause It.s not matched some.. sorry But I Tried Best :3
Level Support : Robtop / Dudex / DestructorGD / N4XOL
♬ Partition More Video List
◆ Random Story? In Geometry Dash : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqPVpZRBKGG6emqQy5Gq4fb
◆ Geometry Dash Song / Bgm FULL TIME LEVEL : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqpZC0--vswOUr7E9qGVfeO
◆ Geometry Dash Mad Movie : https://www.youtube.com/playlist?list=PLxLTiR9IMRqrygjhMOLw8N1_9y-0LKH7L
◆ Geometry Dash Series Level / Top 5~10 : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqD8RbCorTZZtIpjmbbDdQW
◆ Geometry Dash Rhythm Game Cover (My Special? Work) : http://www.youtube.com/playlist?list=PLxLTiR9IMRqpWy-KJmELSSzWUubXny8yK
◆ Geometry Dash My Favorite Level / Cool Level : http://www.youtube.com/playlist?list=PLxLTiR9IMRqo7UEjh8aRvuig-jUjW2pkn
◆ My Demon Clear List : http://www.youtube.com/playlist?list=PLxLTiR9IMRqo_y_1QQZ-TkLDycZkYXhEh
◆ Geometry Dash My Creator Tutorial (How To Make~) : http://www.youtube.com/playlist?list=PLxLTiR9IMRqr44lnsCauQcICsPOjEBF6Z
◆ Geometry Dash Demon IF Series : http://www.youtube.com/playlist?list=PLxLTiR9IMRqrg2p5aNBw7v-WgtOUXw93z
◆ Geometry Dash Official Level Remix : http://www.youtube.com/playlist?list=PLxLTiR9IMRqpXUUDpjrzY9WsFWOe8ye3U
◆ Partition Geometry Dash Challenge : http://www.youtube.com/playlist?list=PLxLTiR9IMRqqB-WFgKjXbCkGDVIBfr9eC
◆ Geometry Dash Official Level Robot Ver : http://www.youtube.com/playlist?list=PLxLTiR9IMRqp_3b974QRpAoTEZw51rh0j
◆ Geometry Dash 2.1 Info / Fan Made Level : http://www.youtube.com/playlist?list=PLxLTiR9IMRqo36r1uDxmsFPjEtfBsWMJ8
◆ Geometry Dash Secret Way / Free Star Level : http://www.youtube.com/playlist?list=PLxLTiR9IMRqq-sl5bwVZ3m4M0nmchfa4d
Geometry Dash / 지오메트리대쉬 / Partition / 파티션 / 시온 / Sion / ジオメトリダッシュ / 지오메트리대쉬 2.0 / 핑거뱅 / Geometry Dash FingerBang
- published: 20 Apr 2016
- views: 668
Maths By Amiya Geometry 3 Similarity 1 Parallel Lines in Triangle
- Order: Reorder
- Duration: 7:27
- Updated: 16 Apr 2016
- views: 126
Application of Parallel lines in triangle
If in ∆ ABC , points D, F & H are on side AB & E, G & I are on side AC BC || DE || FG || HI and AH=HF=FD=DB then what...
Application of Parallel lines in triangle
If in ∆ ABC , points D, F & H are on side AB & E, G & I are on side AC BC || DE || FG || HI and AH=HF=FD=DB then what is the area ratio of ∎DEIH to that of ∎BCGF
wn.com/Maths By Amiya Geometry 3 Similarity 1 Parallel Lines In Triangle
Application of Parallel lines in triangle
If in ∆ ABC , points D, F & H are on side AB & E, G & I are on side AC BC || DE || FG || HI and AH=HF=FD=DB then what is the area ratio of ∎DEIH to that of ∎BCGF
- published: 16 Apr 2016
- views: 126
Geometry Dash (Very Easy Demon) - Parallel World - by lRabb2tl
- Order: Reorder
- Duration: 1:24
- Updated: 16 Apr 2016
- views: 2
lel this level made me remember too much stuff.
Level ID: 79939
https://everyplay.com/videos/28178158
Video recorded with Everyplay. Download Geometry Dash on ...
lel this level made me remember too much stuff.
Level ID: 79939
https://everyplay.com/videos/28178158
Video recorded with Everyplay. Download Geometry Dash on the App Store: https://itunes.apple.com/app/id625334537
wn.com/Geometry Dash (Very Easy Demon) Parallel World By Lrabb2Tl
lel this level made me remember too much stuff.
Level ID: 79939
https://everyplay.com/videos/28178158
Video recorded with Everyplay. Download Geometry Dash on the App Store: https://itunes.apple.com/app/id625334537
- published: 16 Apr 2016
- views: 2
Paced Geometry (2.3) - Proving Lines Parallel (Part 1 of 2)
- Order: Reorder
- Duration: 6:31
- Updated: 15 Apr 2016
- views: 2
Greetings Everyone, totonbutton here on study mode. In approximately 1 month from this moment will be my EOC for Geometry, and I wanted to prepare, by making yo...
Greetings Everyone, totonbutton here on study mode. In approximately 1 month from this moment will be my EOC for Geometry, and I wanted to prepare, by making youtube videos because I love talking. Hope you find it even a bit helpful.
===================================================
Youtube Channel: https://www.youtube.com/user/ecityzen2
Google+ Account: https://plus.google.com/u/0/b/117019035866834037340/117019035866834037340/posts?pageId=117019035866834037340
I don't have any other Social Media accounts, if you see my account on facebook or twitter or snapchat or instagram or any other social media except the one's viewed here in the description are not me unless I warn you guys. This is a warning to all fakers out there. Thank you and Goodbye, enjoy the video and have a nice life.
wn.com/Paced Geometry (2.3) Proving Lines Parallel (Part 1 Of 2)
Greetings Everyone, totonbutton here on study mode. In approximately 1 month from this moment will be my EOC for Geometry, and I wanted to prepare, by making youtube videos because I love talking. Hope you find it even a bit helpful.
===================================================
Youtube Channel: https://www.youtube.com/user/ecityzen2
Google+ Account: https://plus.google.com/u/0/b/117019035866834037340/117019035866834037340/posts?pageId=117019035866834037340
I don't have any other Social Media accounts, if you see my account on facebook or twitter or snapchat or instagram or any other social media except the one's viewed here in the description are not me unless I warn you guys. This is a warning to all fakers out there. Thank you and Goodbye, enjoy the video and have a nice life.
- published: 15 Apr 2016
- views: 2
-
-
Core 1 - Coordinate Geometry (2) - Parallel and Perpendicular Lines
This channel is managed by up and coming UK maths teachers. Videos designed for the site by Steve Blades, retired Youtuber and owner of m4ths.com to assist learning in UK classrooms. Designed for the Edexcel spec but applicable to AQA, OCR,MEI and WJEC. -
8th Grade: Geometry: Parallel lines, Transverse lines, Triangles & Angles 3/10/14
-
Geometry - Chapter 3 Review (Perpendicular and Parallel Lines)
-
Geometry - Proofs for Triangles
Proofs give students much trouble, so let's give them some trouble back! In this lesson we cover the four main methods of proving triangles congruent, including SSS, SAS, ASA, and AAS. We cover CPCTC as well. In the two proofs covered, one involves parallel lines and the other triangles back to back, using the reflexive property. YAY MATH! Please visit yaymath.org Videos copyright (c) Yay Math -
Core 1 - Coordinate Geometry 5 - Parallel and perpendicular lines (AS and A2 Level Mathematics)
Created by Steve Blades. Lead Teacher of Mathematics and Oftsed rated Outstanding. All videos and worksheets can be found at www.m4ths.com -
-
Geometry - Parallel Line Angle Pairs - 9/18/15
Parallel lines Special Angle Pairs Creating a foldable to study with -
Geometry 3.3 proving lines parallel
Geometry 3.3 proving lines parallel
Geometry - 3.1 - Parallel Lines and Transversals
- Order: Reorder
- Duration: 26:09
- Updated: 29 May 2014
- views: 542
Want a copy of these notes for yourself? PDF versions are available at http://classjump.com/p/paulwagner/?what=classes&class;=203177 under the "NOTES" heading if...
Want a copy of these notes for yourself? PDF versions are available at http://classjump.com/p/paulwagner/?what=classes&class;=203177 under the "NOTES" heading if you'd like to print them out and follow along. Study hard!
wn.com/Geometry 3.1 Parallel Lines And Transversals
Core 1 - Coordinate Geometry (2) - Parallel and Perpendicular Lines
- Order: Reorder
- Duration: 22:46
- Updated: 23 Aug 2013
- views: 15433
This channel is managed by up and coming UK maths teachers. Videos designed for the site by Steve Blades, retired Youtuber and owner of m4ths.com to assist lear...
This channel is managed by up and coming UK maths teachers. Videos designed for the site by Steve Blades, retired Youtuber and owner of m4ths.com to assist learning in UK classrooms.
Designed for the Edexcel spec but applicable to AQA, OCR,MEI and WJEC.
wn.com/Core 1 Coordinate Geometry (2) Parallel And Perpendicular Lines
8th Grade: Geometry: Parallel lines, Transverse lines, Triangles & Angles 3/10/14
- Order: Reorder
- Duration: 25:01
- Updated: 10 Mar 2014
- views: 4910
- published: 10 Mar 2014
- views: 4910
Geometry - Chapter 3 Review (Perpendicular and Parallel Lines)
- Order: Reorder
- Duration: 40:38
- Updated: 28 Jan 2014
- views: 2199
- published: 28 Jan 2014
- views: 2199
Geometry - Proofs for Triangles
- Order: Reorder
- Duration: 25:39
- Updated: 19 Oct 2012
- views: 117705
Proofs give students much trouble, so let's give them some trouble back! In this lesson we cover the four main methods of proving triangles congruent, including...
Proofs give students much trouble, so let's give them some trouble back! In this lesson we cover the four main methods of proving triangles congruent, including SSS, SAS, ASA, and AAS. We cover CPCTC as well. In the two proofs covered, one involves parallel lines and the other triangles back to back, using the reflexive property. YAY MATH!
Please visit yaymath.org
Videos copyright (c) Yay Math
wn.com/Geometry Proofs For Triangles
Proofs give students much trouble, so let's give them some trouble back! In this lesson we cover the four main methods of proving triangles congruent, including SSS, SAS, ASA, and AAS. We cover CPCTC as well. In the two proofs covered, one involves parallel lines and the other triangles back to back, using the reflexive property. YAY MATH!
Please visit yaymath.org
Videos copyright (c) Yay Math
- published: 19 Oct 2012
- views: 117705
Core 1 - Coordinate Geometry 5 - Parallel and perpendicular lines (AS and A2 Level Mathematics)
- Order: Reorder
- Duration: 21:23
- Updated: 03 Apr 2015
- views: 526
Created by Steve Blades. Lead Teacher of Mathematics and Oftsed rated Outstanding.
All videos and worksheets can be found at www.m4ths.com
Created by Steve Blades. Lead Teacher of Mathematics and Oftsed rated Outstanding.
All videos and worksheets can be found at www.m4ths.com
wn.com/Core 1 Coordinate Geometry 5 Parallel And Perpendicular Lines (As And A2 Level Mathematics)
Created by Steve Blades. Lead Teacher of Mathematics and Oftsed rated Outstanding.
All videos and worksheets can be found at www.m4ths.com
- published: 03 Apr 2015
- views: 526
Geometry Chapter 3-2 Properties of Parallel Lines
- Order: Reorder
- Duration: 22:40
- Updated: 02 Feb 2015
- views: 95
Geometry Chapter 3-2 Properties of Parallel Lines
Geometry Chapter 3-2 Properties of Parallel Lines
wn.com/Geometry Chapter 3 2 Properties Of Parallel Lines
Geometry - Parallel Line Angle Pairs - 9/18/15
- Order: Reorder
- Duration: 35:33
- Updated: 20 Sep 2015
- views: 33
Parallel lines
Special Angle Pairs
Creating a foldable to study with
- published: 20 Sep 2015
- views: 33
Geometry 3.3 proving lines parallel
- Order: Reorder
- Duration: 31:07
- Updated: 19 Sep 2012
- views: 380
Geometry 3.3 proving lines parallel
Geometry 3.3 proving lines parallel
wn.com/Geometry 3.3 Proving Lines Parallel
close fullscreen
- Playlist
- Chat
close fullscreen
- Playlist
- Chat
3:31
Geometry Help from MathHelp.com - Parallel Lines
MathHelp.com offers comprehensive geometry help with a personal math teacher. In this sam...
published: 21 Jan 2008
Geometry Help from MathHelp.com - Parallel Lines
Geometry Help from MathHelp.com - Parallel Lines
- Report rights infringement
- published: 21 Jan 2008
- views: 65719
2:08
Parallel and perpendicular lines intro | Analytic geometry | Geometry | Khan Academy
Do the two lines intersect or stay apart? If they intersect, do they do so thereby creatin...
published: 17 Jul 2015
Parallel and perpendicular lines intro | Analytic geometry | Geometry | Khan Academy
Parallel and perpendicular lines intro | Analytic geometry | Geometry | Khan Academy
- Report rights infringement
- published: 17 Jul 2015
- views: 111135
34:33
Geometry - Parallel Lines and Transversals
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in...
published: 26 Feb 2013
Geometry - Parallel Lines and Transversals
Geometry - Parallel Lines and Transversals
- Report rights infringement
- published: 26 Feb 2013
- views: 48724
9:44
Geometry - Parallel Lines and Transversals
Parallel Lines is a main topic in Geometry, and comes up many times on the SAT. Join us in...
published: 30 Oct 2009
Geometry - Parallel Lines and Transversals
Geometry - Parallel Lines and Transversals
- Report rights infringement
- published: 30 Oct 2009
- views: 33946
7:08
Angles formed by parallel lines and transversals | Geometry | Khan Academy
Parallel lines, transversal lines, corresponding angles
Practice this lesson yourself on ...
published: 21 Sep 2011
Angles formed by parallel lines and transversals | Geometry | Khan Academy
Angles formed by parallel lines and transversals | Geometry | Khan Academy
- Report rights infringement
- published: 21 Sep 2011
- views: 399571
7:53
Angles formed between transversals and parallel lines | Geometry | Khan Academy
Angles of parallel lines
Watch the next lesson: https://www.khanacademy.org/math/geometry...
published: 09 Aug 2010
Angles formed between transversals and parallel lines | Geometry | Khan Academy
Angles formed between transversals and parallel lines | Geometry | Khan Academy
- Report rights infringement
- published: 09 Aug 2010
- views: 148707
3:35
Identifying parallel and perpendicular lines | Geometry | Khan Academy
Let's now apply what we learned and do an exercise together in which we identify parallel ...
published: 10 Nov 2011
Identifying parallel and perpendicular lines | Geometry | Khan Academy
Identifying parallel and perpendicular lines | Geometry | Khan Academy
- Report rights infringement
- published: 10 Nov 2011
- views: 196765
9:39
Geometry: 3-2 Angles formed by Parallel Lines and Transversals
If these helped at all, PRETTY PLEASE Like my Facebook Page: http://facebook.com/tylersoka...
published: 31 Jul 2010
Geometry: 3-2 Angles formed by Parallel Lines and Transversals
Geometry: 3-2 Angles formed by Parallel Lines and Transversals
- Report rights infringement
- published: 31 Jul 2010
- views: 42006
31:58
GCSE Maths - Angles in Parallel Lines - Foundation Higher - Geometry - Linear Edexcel Revision
All videos can be found at www.m4ths.com and www.astarmaths.com
These videos were donated ...
published: 15 Mar 2014
GCSE Maths - Angles in Parallel Lines - Foundation Higher - Geometry - Linear Edexcel Revision
GCSE Maths - Angles in Parallel Lines - Foundation Higher - Geometry - Linear Edexcel Revision
- Report rights infringement
- published: 15 Mar 2014
- views: 11601
2:16
Figuring out angles between transversal and parallel lines | Geometry | Khan Academy
Practice this lesson yourself on KhanAcademy.org right now:
https://www.khanacademy.org/m...
published: 07 Aug 2013
Figuring out angles between transversal and parallel lines | Geometry | Khan Academy
Figuring out angles between transversal and parallel lines | Geometry | Khan Academy
- Report rights infringement
- published: 07 Aug 2013
- views: 153930
5:18
Proof: Corresponding angle equivalence implies parallel lines | Geometry | Khan Academy
Proof by contradiction that corresponding angle equivalence implies parallel lines
Watch ...
published: 22 Sep 2011
Proof: Corresponding angle equivalence implies parallel lines | Geometry | Khan Academy
Proof: Corresponding angle equivalence implies parallel lines | Geometry | Khan Academy
- Report rights infringement
- published: 22 Sep 2011
- views: 100407
9:13
Equations of parallel and perpendicular lines | Analytic geometry | Geometry | Khan Academy
Equations of Parallel and Perpendicular Lines
Practice this lesson yourself on KhanAcadem...
published: 06 Apr 2010
Equations of parallel and perpendicular lines | Analytic geometry | Geometry | Khan Academy
Equations of parallel and perpendicular lines | Analytic geometry | Geometry | Khan Academy
- Report rights infringement
- published: 06 Apr 2010
- views: 409438
close fullscreen
- Playlist
- Chat
15:01
Geometry - Parallel Lines and Transversals; Angle Relationships SOL Review
published: 12 May 2016
Geometry - Parallel Lines and Transversals; Angle Relationships SOL Review
Geometry - Parallel Lines and Transversals; Angle Relationships SOL Review
- Report rights infringement
- published: 12 May 2016
- views: 1
2:01
How to draw a parallel through any point using a compass
Constructing a parallel through a point.
This YouTube channel is dedicated to teaching pe...
published: 12 May 2016
How to draw a parallel through any point using a compass
How to draw a parallel through any point using a compass
- Report rights infringement
- published: 12 May 2016
- views: 16
1:45
Geometry final. Geometry in the real world 2016
Geometry final. Geometry in the real world.
parallel lines in the main gym on the floor
p...
published: 09 May 2016
Geometry final. Geometry in the real world 2016
Geometry final. Geometry in the real world 2016
- Report rights infringement
- published: 09 May 2016
- views: 13
0:16
Download [PDF] Vectors and Coordinate Geometry
detail http://book99download.com/readbook.php?asin=1523688661.html Vectors and Coordinate ...
published: 08 May 2016
Download [PDF] Vectors and Coordinate Geometry
Download [PDF] Vectors and Coordinate Geometry
- Report rights infringement
- published: 08 May 2016
- views: 0
0:16
Vectors and Coordinate Geometry
detail link :: http://book99download.com/readbook.php?asin=1523688661.html Vectors and Coo...
published: 06 May 2016
Vectors and Coordinate Geometry
Vectors and Coordinate Geometry
- Report rights infringement
- published: 06 May 2016
- views: 0
23:58
Geometry SOL Review RC1 Part 2: Proving Lines Parallel
Geometry 2015-16 SOL Review
Reporting Category 1: Reasoning, Lines, and Transformations
Pa...
published: 02 May 2016
Geometry SOL Review RC1 Part 2: Proving Lines Parallel
Geometry SOL Review RC1 Part 2: Proving Lines Parallel
- Report rights infringement
- published: 02 May 2016
- views: 79
1:09
Geometry dash - [2.0] - [Demon] - Parallel Run By Dhafin - TheJaco9
Demon difficultly: 2/10★ (Very easy demon)
-------------------------------------------...
published: 01 May 2016
Geometry dash - [2.0] - [Demon] - Parallel Run By Dhafin - TheJaco9
Geometry dash - [2.0] - [Demon] - Parallel Run By Dhafin - TheJaco9
- Report rights infringement
- published: 01 May 2016
- views: 6
1:43
Geometry Dash - Parallel World (Very Easy Demon) by IRabb2tI
Demon Count: 17
published: 22 Apr 2016
Geometry Dash - Parallel World (Very Easy Demon) by IRabb2tI
Geometry Dash - Parallel World (Very Easy Demon) by IRabb2tI
- Report rights infringement
- published: 22 Apr 2016
- views: 27
1:34
Geometry Dash 2.1 VS 2.0? : All Sneak Peek + All Fan Made (Parallel)
♬ Geometry Dash 2.1 VS 2.0 (?) Fan Made And Real Sneak Peek (FireBall + FingerBang + Spide...
published: 20 Apr 2016
Geometry Dash 2.1 VS 2.0? : All Sneak Peek + All Fan Made (Parallel)
Geometry Dash 2.1 VS 2.0? : All Sneak Peek + All Fan Made (Parallel)
- Report rights infringement
- published: 20 Apr 2016
- views: 668
7:27
Maths By Amiya Geometry 3 Similarity 1 Parallel Lines in Triangle
Application of Parallel lines in triangle
If in ∆ ABC , points D, F & H are on side AB & ...
published: 16 Apr 2016
Maths By Amiya Geometry 3 Similarity 1 Parallel Lines in Triangle
Maths By Amiya Geometry 3 Similarity 1 Parallel Lines in Triangle
- Report rights infringement
- published: 16 Apr 2016
- views: 126
1:24
Geometry Dash (Very Easy Demon) - Parallel World - by lRabb2tl
lel this level made me remember too much stuff.
Level ID: 79939
https://everyplay.com/vid...
published: 16 Apr 2016
Geometry Dash (Very Easy Demon) - Parallel World - by lRabb2tl
Geometry Dash (Very Easy Demon) - Parallel World - by lRabb2tl
- Report rights infringement
- published: 16 Apr 2016
- views: 2
6:31
Paced Geometry (2.3) - Proving Lines Parallel (Part 1 of 2)
Greetings Everyone, totonbutton here on study mode. In approximately 1 month from this mom...
published: 15 Apr 2016
Paced Geometry (2.3) - Proving Lines Parallel (Part 1 of 2)
Paced Geometry (2.3) - Proving Lines Parallel (Part 1 of 2)
- Report rights infringement
- published: 15 Apr 2016
- views: 2
close fullscreen
- Playlist
- Chat
26:09
Geometry - 3.1 - Parallel Lines and Transversals
Want a copy of these notes for yourself? PDF versions are available at http://classjump.co...
published: 29 May 2014
Geometry - 3.1 - Parallel Lines and Transversals
Geometry - 3.1 - Parallel Lines and Transversals
- Report rights infringement
- published: 29 May 2014
- views: 542
22:46
Core 1 - Coordinate Geometry (2) - Parallel and Perpendicular Lines
This channel is managed by up and coming UK maths teachers. Videos designed for the site b...
published: 23 Aug 2013
Core 1 - Coordinate Geometry (2) - Parallel and Perpendicular Lines
Core 1 - Coordinate Geometry (2) - Parallel and Perpendicular Lines
- Report rights infringement
- published: 23 Aug 2013
- views: 15433
25:01
8th Grade: Geometry: Parallel lines, Transverse lines, Triangles & Angles 3/10/14
published: 10 Mar 2014
8th Grade: Geometry: Parallel lines, Transverse lines, Triangles & Angles 3/10/14
8th Grade: Geometry: Parallel lines, Transverse lines, Triangles & Angles 3/10/14
- Report rights infringement
- published: 10 Mar 2014
- views: 4910
40:38
Geometry - Chapter 3 Review (Perpendicular and Parallel Lines)
published: 28 Jan 2014
Geometry - Chapter 3 Review (Perpendicular and Parallel Lines)
Geometry - Chapter 3 Review (Perpendicular and Parallel Lines)
- Report rights infringement
- published: 28 Jan 2014
- views: 2199
25:39
Geometry - Proofs for Triangles
Proofs give students much trouble, so let's give them some trouble back! In this lesson we...
published: 19 Oct 2012
Geometry - Proofs for Triangles
Geometry - Proofs for Triangles
- Report rights infringement
- published: 19 Oct 2012
- views: 117705
21:23
Core 1 - Coordinate Geometry 5 - Parallel and perpendicular lines (AS and A2 Level Mathematics)
Created by Steve Blades. Lead Teacher of Mathematics and Oftsed rated Outstanding.
All vid...
published: 03 Apr 2015
Core 1 - Coordinate Geometry 5 - Parallel and perpendicular lines (AS and A2 Level Mathematics)
Core 1 - Coordinate Geometry 5 - Parallel and perpendicular lines (AS and A2 Level Mathematics)
- Report rights infringement
- published: 03 Apr 2015
- views: 526
22:40
Geometry Chapter 3-2 Properties of Parallel Lines
Geometry Chapter 3-2 Properties of Parallel Lines
published: 02 Feb 2015
Geometry Chapter 3-2 Properties of Parallel Lines
Geometry Chapter 3-2 Properties of Parallel Lines
- Report rights infringement
- published: 02 Feb 2015
- views: 95
35:33
Geometry - Parallel Line Angle Pairs - 9/18/15
Parallel lines
Special Angle Pairs
Creating a foldable to study with
published: 20 Sep 2015
Geometry - Parallel Line Angle Pairs - 9/18/15
Geometry - Parallel Line Angle Pairs - 9/18/15
- Report rights infringement
- published: 20 Sep 2015
- views: 33
31:07
Geometry 3.3 proving lines parallel
Geometry 3.3 proving lines parallel
published: 19 Sep 2012
Geometry 3.3 proving lines parallel
Geometry 3.3 proving lines parallel
- Report rights infringement
- published: 19 Sep 2012
- views: 380
Geometry - 3.1 - Parallel Lines and Transversals...
Core 1 - Coordinate Geometry (2) - Parallel and Pe...
8th Grade: Geometry: Parallel lines, Transverse l...
Geometry - Chapter 3 Review (Perpendicular and Par...
Geometry - Proofs for Triangles...
Core 1 - Coordinate Geometry 5 - Parallel and perp...
Geometry Chapter 3-2 Properties of Parallel Lines...
Geometry - Parallel Line Angle Pairs - 9/18/15...
Geometry 3.3 proving lines parallel...
photo: AP / Jason Reed, Pool
Netanyahu Tells Officials 'It's About Time' For Abbas To Accept Peace Talk Offer
Edit WorldNews.com 12 May 2016
Declaring, “It’s about time,” Israeli Prime Minister Benjamin Netanyahu urged heads of diplomatic missions and religious communities on Thursday to encourage Palestinian Authority President Mahmoud Abbas to accept his offer to talk peace, The Jerusalem Post reported.Netanyahu said he is willing to sit down with Abbas in Jerusalem, Ramallah or anywhere else he might be willing to meet....
photo: US Army / 1st Class Peter Lewis
US navy fires officer in charge of sailors held by Iran
Edit The Times of India 13 May 2016
WASHINGTON. The officer in charge of 10 US sailors who were briefly captured by Iran in the Persian Gulf was relieved of his command, the Navy announced ... Navy spokesman Lieutenant Commander Tim Hawkins said other sailors have also been held accountable, but he would not say who these were because the incident remains under investigation ... ....
photo: Creative Commons / Bobby L. Warren
Texas Republicans Approve Measure To Secede From Union
Edit WorldNews.com 12 May 2016
Texas Republicans have succeeded in putting a measure up to secede from the United States at their convention this week, an Inquisitr report said Thursday.Pro-secession group Texas Nationalist Movement told Carbonated.TV in a press release the Republican Party of Texas seeks independence from the rest of the nation by seceding from the Union. The Republican Party’s vote for Texas secession passed with two-thirds of the vote....
photo: AP / Chris Jackson/Pool, File via AP
British 'barbarians' need manners lessons, says Chinese paper on rudeness row
Edit The Times of India 12 May 2016
BEIJING. The British media is riddled with "barbarians" who would benefit from a lesson in manners from China's ancient civilisation, a state-run newspaper said Thursday after Queen Elizabeth II called some Chinese officials "very rude" ... The remarks made headlines worldwide on Wednesday but initially they were largely censored in China, blacked out of BBC World transmissions, according to the British broadcaster ... "Extraordinary!" ... ....
photo: AP / Hezbollah Media Department
Top Hezbollah commander Badreddine killed in Israel strike
Edit BBC News 13 May 2016
A senior Hezbollah commander has been killed in an Israeli operation in Syria, the Lebanon-based Shia militant organisation says. It says Mustafa Amine Badreddine died in an Israeli air strike near Damascus airport. Israel has so far made no public comment on the claim ... Announcing Badreddine's death, Hezbollah said in a statement ... Share this story About sharing. ....
« back to news headlines
Neck-and-neck battle in Angamaly
Edit The Hindu 13 May 2016
National leadership ... Shibu, CPI (M) area secretary. Besides the bypass project, the proposal for a parallel bridge at Kalady and development of the Angamaly Taluk Hospital also tops the LDF’s poll promises. The UDF, on the other hand, is also banking on the development poll plank with the promises of Angamaly Bypass and Parallel Bridge at Kalady topping its list as well ... Shaji, Angamaly block president of the Congress ... ....
U.N. Security Council removes Libyan oil tanker from blacklist
Edit Yahoo Daily News 13 May 2016
By Louis Charbonneau. UNITED NATIONS (Reuters) - The United Nations Security Council on Thursday removed from a U.N ... The tanker Distya Ameya was added to a list of vessels under sanctions last month after the rival eastern government's parallel oil company attempted to use it to ship a cargo of 650,000 barrels of crude. The U.N ... The eastern administration has set up its own National Oil Corporation in parallel to the Tripoli-based NOC....
U.N. Security Council removes Indian-flagged oil tanker from blacklist
Edit Yahoo Daily News 13 May 2016
By Louis Charbonneau. UNITED NATIONS (Reuters) - The United Nations Security Council on Thursday removed from a U.N ... The tanker Distya Ameya was added to a list of vessels under sanctions last month after the rival eastern government's parallel oil company attempted to use it to ship a cargo of 650,000 barrels of crude. The U.N ... The eastern administration has set up its own National Oil Corporation in parallel to the Tripoli-based NOC....
ALPHAMIN ANNOUNCES A 34% INCREASE IN… (Alphamin Resources Corp)
Edit Public Technologies 13 May 2016
(Source. Alphamin Resources Corp). ALPHAMIN ANNOUNCES A 34% INCREASE IN MEASURED AND INDICATED MINERAL RESOURCES FOR ITS BISIE TIN PROJECT, DRC. UPDATE HIGHLIGHTS. • The updated Mineral Resource includes. ... • The tin mineralisation has a strong chute geometry with a high grade chute interpreted to plunge to the north and is open at depth. • The mineral resource was defined over 700m down plunge and has a vertical depth of 550m ... (noodl....
Foreign genes in H. dujardini genome assemblies [Letters (Online Only)]>
Edit PNAS 13 May 2016
Our report (1) describing the discovery of extensive horizontal gene transfer in a tardigrade genome has raised questions from other groups who were sequencing the Hypsibius dujardini genome in parallel or who have done new experiments and analyses since our report (2–5). Bemm et al. (2) now report filtering our... ....
Arab coalition ‘will advance on Sana’a if talks fail’
Edit Gulf News 13 May 2016
Military option runs parallel to the political process, says spokesman ... ....
Uber’s quasi union could be a Faustian bargain for drivers (UTS - University of Technology, Sydney)
Edit Public Technologies 13 May 2016
(Source. UTS - University of Technology, Sydney) ... Uber will make US$100 million in payments to those involved in the case ... That the Guild is company sponsored evokes parallels with 'yellow' or company unions that sprung up in the US in the 1930s as an attempt to circumvent the labour provisions of Roosevelt's New Deal ... The parallel with Uber's approach to the emerging groups of drivers across the world, including Australia, is obvious....
Album of the Week: Overhead, the Albatross – Learning to Growl
Edit The Irish Times 13 May 2016
That’s the theory, anyway, but it’s one that has clearly bypassed Dublin band Overhead, The Albatross ... Factor in ambient vocals (Emilie Daly), strings (viola, violin, cello) and brass (trumpet, trombone, saxophone), and you have a complete layered package that delivers on dynamics, which in turn run parallel with responsive experimentation ... overheadthealbatross.com ....
CERN LHC Opens Mysterious Cloud Portal Anomaly In The Sky Over Switzerland, Conspiracy Theorists Raise ...
Edit Inquisitr 13 May 2016
Others have expressed fears that it could open a portal to another dimension allowing evil demonic entities or alien beings from a parallel universe to gain access to our world ... The 666 symbol, according to doomsday theorists, is proof that the Devil is using CERN to open a portal to a parallel universe so that demonic cohorts can gain access to our universe and take control ... [Photo By Martial Trezzini/AP] ... The Inquisitr News ....
Kerala ex-CM used Somalia analogy too
Edit The Times of India 13 May 2016
Thiruvananthapuram. PM Narendra Modi wasn't the first politician to draw parallels between the living conditions of Kerala's tribals and those of Somalia. Communist veteran V S Achuthanandan had used a similar analogy in 2013 after he visited Attapadi following child deaths there. He had drawn the government's attention to "Somalia-type" conditions in the tribal hamlets ... Communists only promoted har tals and Congress corruption ... ....
'State govt is creating a legacy in concrete'
Edit The Times of India 13 May 2016
Hyderabad ... The project will only increase the inconvenience already being posed by the ongoing metro works." ... Drawing parallels with the upcoming capital of Andhra Pradesh, Mohan Mahadevrao said, "Deforestation and axing of trees in the name of metro, industrialisation and SRDP works in the city is a matter of great concern for the people living in the suburban areas of Hyderabad ... ....
Ex-Kerala CM used Somalia analogy too
Edit The Times of India 13 May 2016
THIRUVANANTHAPURAM. PM Narendra Modi wasn't the first politician to draw parallels between the living conditions of Kerala's tribals and those of Somalia. Communist veteran VS Achuthanandan had used a similar analogy in 2013 after he visited Attapadi following child deaths there, drawing the government's attention to "Somalia-type" conditions here ... Chandy also said he'd approach the election commission on the issue ... RELATED....
Art review: Sarah Tomasetti: Influxus at Beaver Galleries
Edit Sydney Morning Herald 13 May 2016
Influxus by Sarah Tomasetti. Beaver Galleries, 81 Denison Street, Deakin. Until May 22. Reviewer. Sasha Grishin ... Advertisement ... It is a very beautiful technique with a subdued palette and a rich glowing inner luminosity ... Central to her practice is the concept of global warming, and as the great snow caps melt and disintegrate, she draws a parallel with the natural cracking found in the fresco surface. She continues ... ... ....
- 1
- 2
- 3
- 4
- 5
- Next page »
