- published: 17 Jun 2013
- views: 58878
-
remove the playlistGini Coefficient
- remove the playlistGini Coefficient
- published: 05 Oct 2011
- views: 45678
- published: 14 Feb 2016
- views: 25
- published: 23 Sep 2014
- views: 27057
- published: 16 Dec 2014
- views: 4846
- published: 21 Jan 2016
- views: 649
- published: 08 May 2015
- views: 100
- published: 31 Dec 2013
- views: 19901

The Gini coefficient (also known as the Gini index or Gini ratio) is a measure of statistical dispersion developed by the Italian statistician and sociologist Corrado Gini and published in his 1912 paper "Variability and Mutability" (Italian: Variabilità e mutabilità).
The Gini coefficient measures the inequality among values of a frequency distribution (for example levels of income). A Gini coefficient of zero expresses perfect equality where all values are the same (for example, where everyone has an exactly equal income). A Gini coefficient of one (100 on the percentile scale) expresses maximal inequality among values (for example where only one person has all the income).
It has found application in the study of inequalities in disciplines as diverse as sociology, economics, health science, ecology, chemistry, engineering and agriculture. It is commonly used as a measure of inequality of income or wealth. Worldwide, Gini coefficients for income range from approximately 0.23 (Sweden) to 0.70 (Namibia) although not every country has been assessed.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...

-
 4:50
4:50Lorenz Curve and Gini Coefficient
Lorenz Curve and Gini CoefficientLorenz Curve and Gini Coefficient
FREE APP - get all of the videos on this channel on your phone. Put myapp.is/Economics%20Diagrams in your phone web browser and follow the instructions. Income Inequality can be measured graphically by a Lorenz Curve or mathematically using the Gini Coefficient. This video explains how both of these work -
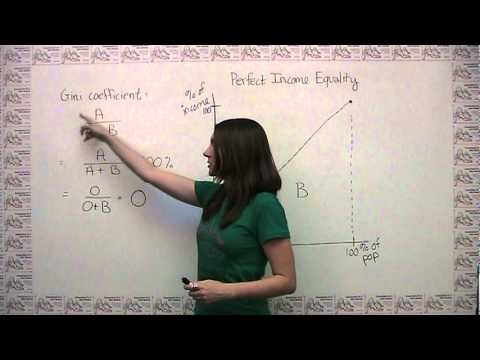 5:46
5:46The Gini Coefficient
The Gini CoefficientThe Gini Coefficient
This video introduces the Gini coefficient, which is a way to summarize income inequality using a single number. For more information and a complete listing of videos and online articles by topic or textbook chapter, see http://www.economistsdoitwithmodels.com/economics-classroom/ For t-shirts and other EDIWM items, see http://www.economistsdoitwithmodels.com/merch/ By Jodi Beggs - Economists Do It With Models http://www.economistsdoitwithmodels.com Facebook: http://www.facebook.com/economistsdoitwithmodels Twitter: http://www.twitter.com/jodiecongirl Tumblr: http://economistsdoitwithmodels.tumblr.com -
 17:18
17:18BEST Econ Tutor - Inequality: Lorenz Curve and Gini Coefficient (Ch 18)
BEST Econ Tutor - Inequality: Lorenz Curve and Gini Coefficient (Ch 18)BEST Econ Tutor - Inequality: Lorenz Curve and Gini Coefficient (Ch 18)
In this module, Rohen Shah discusses inequality. Topics include measuring income using mean and median, calculating inequality using the lorenz curve and gini coefficient, and the difference between progressive and regressive tax structures with tax brackets. For further mastery of the concept, check out our active-learning, customized platform at http://www.BestEconTutor.com -
 9:02
9:02Poverty (The Lorenz Curve and Gini Coefficient)
Poverty (The Lorenz Curve and Gini Coefficient)Poverty (The Lorenz Curve and Gini Coefficient)
-
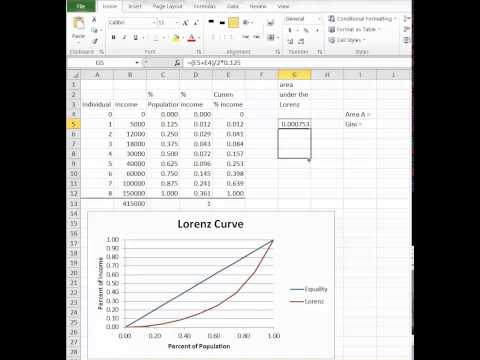 9:33
9:33Gini Index and Lorenz Curve in Excel
Gini Index and Lorenz Curve in ExcelGini Index and Lorenz Curve in Excel
There is an earlier video titled Lorenz Curve in Excel. That video does not include the Gini Index. It focuses on how to construct a Lorenz curve from raw data in Excel. -
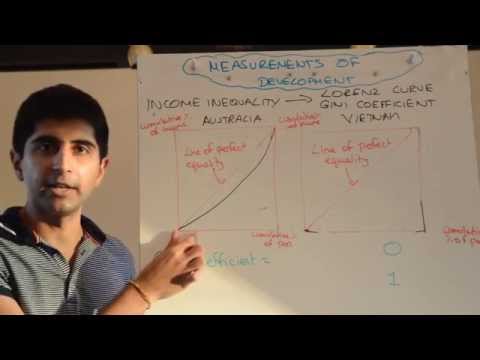 6:54
6:54A2/IB 6) Measures of Development - Lorenz Curve and Gini Coefficient (Income Inequality)
A2/IB 6) Measures of Development - Lorenz Curve and Gini Coefficient (Income Inequality)A2/IB 6) Measures of Development - Lorenz Curve and Gini Coefficient (Income Inequality)
A2/IB 6) Measures of Development - Lorenz Curve and Gini Coefficient (Income Inequality) - An understanding of the Lorenz Curve and Gini Coefficient to measure income inequality and thus measure development progress of a given economy -
 11:13
11:13Equity in the Distribution of Income Series: The Gini Coefficient
Equity in the Distribution of Income Series: The Gini CoefficientEquity in the Distribution of Income Series: The Gini Coefficient
Hey Everyone, This is video 5 of 8 videos in “The Equity in the Distribution of Income Series”. Watch the entire series right here: https://www.youtube.com/playlist?list=PLNI2Up0JUWkEFqlgvMNOhJ3pei2zXyuhD As a teacher of IB Economics in Santiago, Chile, these videos were created to help students navigate their way through their two-year course of study. I have made these videos public in the hope that they might be helpful to other Economics students around the world. Check out all of the Macroeconomic playlists… Fundamentals of Macroeconomics Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkG6AmW4E2YNV_hBP0AVuw4v Aggregate Demand and Aggregate Supply Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkGyyUCGXdTWNgfkKJ9_0l6q Macroeconomic Equilibrium Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkGZBoaxdZHC9mokrwtXT4Xg Low Unemployment Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkFCxtc5-8q_AJseZFYbVeA4 Low and Stable Rate of Inflation Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkGfCtnjSTIPQhZkZxzZM2Pf Economic Growth Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkFxkSsb8p3fCrx0Z3i59REX Equity in the Distribution of Income Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkEFqlgvMNOhJ3pei2zXyuhD Fiscal Policy Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkGCPnKi4Er5FH8s_SV_WXH3 Monetary Policy Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkFCISVn47ZJzL7qx291zlS7 Supply-Side Policies Series https://www.youtube.com/playlist?list=PLNI2Up0JUWkGczuu4Frzrw9oBgp2GU4e5 Enjoy! Brad -
 6:06
6:06Gini Coefficient | What is Income Inequality?
Gini Coefficient | What is Income Inequality?Gini Coefficient | What is Income Inequality?
Come learn about the Gini Coefficient in a fun, exciting way! Music used does not belong to us, it is used for creative purposes. -
 1:17
1:17Gini Coefficient
Gini Coefficient -
 5:23
5:23Gini Index Calculation from a Lorenz Function
Gini Index Calculation from a Lorenz FunctionGini Index Calculation from a Lorenz Function
This video shows how to calculate the Gini Index that corresponds to a given Lorenz function, using either the fundamental theorem of calculus or the function integration (fnInt) command on a TI83 graphing calculator. The meaning of the Gini Index is also explained.
- Agriculture
- Angus Deaton
- Area
- Atkinson index
- Barter
- Biodiversity
- Canada
- Chemistry
- Consistent estimator
- Corrado Gini
- Credit rating
- Credit risk
- Differentiable
- Ecology
- Economic inequality
- Economics
- Economy of Mexico
- Egalitarianism
- Engineering
- Estimator
- Food stamps
- Gini coefficient
- Health science
- Herfindahl index
- Household
- Household income
- Human Poverty Index
- Information entropy
- Integral
- Interpolation
- Italian language
- Italian people
- JSTOR
- Living wage
- Lorenz curve
- Mann–Whitney U
- Mathematica
- Mathematics
- Mean
- Mean difference
- Nature (journal)
- Normal distribution
- Pareto distribution
- Per capita income
- Piecewise
- Princeton University
- PubMed Central
- PubMed Identifier
- Purchasing power
- Quality of life
- Random distribution
- Ratio
- Ratio analysis
- Robin Hood index
- ROC analysis
- Simpson's rule
- Social welfare
- Sociology
- Statistics
- Subsistence farming
- Suits index
- Sweden
- Theil Index
- Trapezoidal rule
- United States
- Wealth condensation
- Welfare economics
- Wikipedia Link rot
- WP references
- WP Verifiability
-

Lorenz Curve and Gini Coefficient
FREE APP - get all of the videos on this channel on your phone. Put myapp.is/Economics%20Diagrams in your phone web browser and follow the instructions. Income Inequality can be measured graphically by a Lorenz Curve or mathematically using the Gini Coefficient. This video explains how both of these work -

The Gini Coefficient
This video introduces the Gini coefficient, which is a way to summarize income inequality using a single number. For more information and a complete listing of videos and online articles by topic or textbook chapter, see http://www.economistsdoitwithmodels.com/economics-classroom/ For t-shirts and other EDIWM items, see http://www.economistsdoitwithmodels.com/merch/ By Jodi Beggs - Economists Do It With Models http://www.economistsdoitwithmodels.com Facebook: http://www.facebook.com/economistsdoitwithmodels Twitter: http://www.twitter.com/jodiecongirl Tumblr: http://economistsdoitwithmodels.tumblr.com -

BEST Econ Tutor - Inequality: Lorenz Curve and Gini Coefficient (Ch 18)
In this module, Rohen Shah discusses inequality. Topics include measuring income using mean and median, calculating inequality using the lorenz curve and gini coefficient, and the difference between progressive and regressive tax structures with tax brackets. For further mastery of the concept, check out our active-learning, customized platform at http://www.BestEconTutor.com -

Poverty (The Lorenz Curve and Gini Coefficient)
-

Gini Index and Lorenz Curve in Excel
There is an earlier video titled Lorenz Curve in Excel. That video does not include the Gini Index. It focuses on how to construct a Lorenz curve from raw data in Excel. -

A2/IB 6) Measures of Development - Lorenz Curve and Gini Coefficient (Income Inequality)
A2/IB 6) Measures of Development - Lorenz Curve and Gini Coefficient (Income Inequality) - An understanding of the Lorenz Curve and Gini Coefficient to measure income inequality and thus measure development progress of a given economy -

Equity in the Distribution of Income Series: The Gini Coefficient
Hey Everyone, This is video 5 of 8 videos in “The Equity in the Distribution of Income Series”. Watch the entire series right here: https://www.youtube.com/playlist?list=PLNI2Up0JUWkEFqlgvMNOhJ3pei2zXyuhD As a teacher of IB Economics in Santiago, Chile, these videos were created to help students navigate their way through their two-year course of study. I have made these videos public in the hope that they might be helpful to other Economics students around the world. Check out all of the Macroeconomic playlists… Fundamentals of Macroeconomics Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkG6AmW4E2YNV_hBP0AVuw4v Aggregate Demand and Aggregate Supply Series: https://www.youtube.com/playlist?list=PLNI2Up0JUWkGyyUCGXdTWNgfkKJ9_0l6q Macroeconomic Equilibrium Series: https:/... -

Gini Coefficient | What is Income Inequality?
Come learn about the Gini Coefficient in a fun, exciting way! Music used does not belong to us, it is used for creative purposes. -

-

Gini Index Calculation from a Lorenz Function
This video shows how to calculate the Gini Index that corresponds to a given Lorenz function, using either the fundamental theorem of calculus or the function integration (fnInt) command on a TI83 graphing calculator. The meaning of the Gini Index is also explained.
Lorenz Curve and Gini Coefficient
- Order: Reorder
- Duration: 4:50
- Updated: 17 Jun 2013
- views: 58878
- published: 17 Jun 2013
- views: 58878
The Gini Coefficient
- Order: Reorder
- Duration: 5:46
- Updated: 05 Oct 2011
- views: 45678
- published: 05 Oct 2011
- views: 45678
BEST Econ Tutor - Inequality: Lorenz Curve and Gini Coefficient (Ch 18)
- Order: Reorder
- Duration: 17:18
- Updated: 14 Feb 2016
- views: 25
- published: 14 Feb 2016
- views: 25
Poverty (The Lorenz Curve and Gini Coefficient)
- Order: Reorder
- Duration: 9:02
- Updated: 04 Nov 2015
- views: 285
- published: 04 Nov 2015
- views: 285
Gini Index and Lorenz Curve in Excel
- Order: Reorder
- Duration: 9:33
- Updated: 23 Sep 2014
- views: 27057
- published: 23 Sep 2014
- views: 27057
A2/IB 6) Measures of Development - Lorenz Curve and Gini Coefficient (Income Inequality)
- Order: Reorder
- Duration: 6:54
- Updated: 16 Dec 2014
- views: 4846
- published: 16 Dec 2014
- views: 4846
Equity in the Distribution of Income Series: The Gini Coefficient
- Order: Reorder
- Duration: 11:13
- Updated: 21 Jan 2016
- views: 649
- published: 21 Jan 2016
- views: 649
Gini Coefficient | What is Income Inequality?
- Order: Reorder
- Duration: 6:06
- Updated: 08 May 2015
- views: 100
- published: 08 May 2015
- views: 100
Gini Coefficient
- Order: Reorder
- Duration: 1:17
- Updated: 04 Mar 2012
- views: 2374
Gini Index Calculation from a Lorenz Function
- Order: Reorder
- Duration: 5:23
- Updated: 31 Dec 2013
- views: 19901
- published: 31 Dec 2013
- views: 19901
- Playlist
- Chat
- Playlist
- Chat

Lorenz Curve and Gini Coefficient
- Report rights infringement
- published: 17 Jun 2013
- views: 58878

The Gini Coefficient
- Report rights infringement
- published: 05 Oct 2011
- views: 45678

BEST Econ Tutor - Inequality: Lorenz Curve and Gini Coefficient (Ch 18)
- Report rights infringement
- published: 14 Feb 2016
- views: 25

Poverty (The Lorenz Curve and Gini Coefficient)
- Report rights infringement
- published: 04 Nov 2015
- views: 285

Gini Index and Lorenz Curve in Excel
- Report rights infringement
- published: 23 Sep 2014
- views: 27057

A2/IB 6) Measures of Development - Lorenz Curve and Gini Coefficient (Income Inequality)
- Report rights infringement
- published: 16 Dec 2014
- views: 4846

Equity in the Distribution of Income Series: The Gini Coefficient
- Report rights infringement
- published: 21 Jan 2016
- views: 649

Gini Coefficient | What is Income Inequality?
- Report rights infringement
- published: 08 May 2015
- views: 100

Gini Coefficient
- Report rights infringement
- published: 04 Mar 2012
- views: 2374

Gini Index Calculation from a Lorenz Function
- Report rights infringement
- published: 31 Dec 2013
- views: 19901
Riots hit South Africa’s capital over mayoral candidate
Edit San Francisco Chronicle 22 Jun 2016Judge: Starbucks May Be In A Latte Of Trouble
Edit WorldNews.com 21 Jun 2016Jaguar Used in Olympic Ceremony Escapes, Shot in Brazil
Edit WorldNews.com 22 Jun 2016Pakistani Man Injured In Acid Attack By Girlfriend Dies
Edit WorldNews.com 21 Jun 2016NKorea test fires two powerful, mid-range missiles
Edit Daily Star Lebanon 22 Jun 2016Don’t look down
Edit The Economist 16 Jun 2016When disaster strikes, should China do more?
Edit IRINnews 08 Jun 2016Behind the rise of income inequality in Indonesia
Edit The Jakarta Post 07 Jun 2016UPND Manifesto: Reducing Inequality
Edit Zambian Economist 07 Jun 2016RI economic slowdown has resulted in more poverty, says Jokowi
Edit Jakarta Post 17 Mar 2016What’s Behind the Rise in Income Inequality? Technology or Class Struggle?
Edit CounterPunch 17 Mar 2016Government Spending Drives Modest Growth Pick-Up in Indonesia (World Bank Group)
Edit Public Technologies 15 Mar 2016Bridging the gap: housing solution would be a good start
Edit South China Morning Post 11 Mar 2016Confusing banking policy and global economic uncertainty
Edit Jakarta Post 10 Mar 2016UNDP declared a fight on poverty, now a go-to partner for SDGs
Edit Jakarta Post 04 Mar 2016America's Go-To Economic Indicator Is Blunt and Obsolete
Edit The Atlantic 02 Mar 2016How Burlington's Creative Class Explains Bernie Sanders
Edit CityLab 01 Mar 2016Inclusive social protection for poverty alleviation
Edit Jakarta Post 01 Mar 2016- 1
- 2
- 3
- 4
- 5
- Next page »







