Lobster-tailed pot helmet

The lobster-tailed pot helmet, also known as the zischagge, horseman's pot and harquebusier's pot, was a type of post-Renaissance combat helmet. It became popular in Europe, especially for cavalry and officers, from c. 1600; it was derived from an Ottoman Turkish helmet type. The helmet gradually fell out of use in most of Europe in the late 17th century; however, the Austrian heavy cavalry retained it for some campaigns as late as the 1780s.

The French term capeline was also used for this helmet, however, usage of this word was not precise. "Capeline" was indiscriminately used to denote various types of hat, and helmets other than the lobster-tailed pot.

Origin

The lobster-tailed pot helmet had an oriental origin, being derived from the Ottoman Turkish 'chichak' (Turkish - çiçek) helmet, which developed in the 16th century. It was adopted by the Christian states of Europe in the early 17th century. The chichak was almost identical to the later European helmets - it had a forward projecting peak, sliding bar nasal, cheekpieces and neck guard; only its tendency to have a conical rather than rounded skull was distinctive. The European derivative of this helmet saw widespread use during the Thirty Years War when it became known as the zischägge, a Germanisation of the original Turkish name.

Secret (deodorant brand)

Secret is an antiperspirant/deodorant for women manufactured by Procter & Gamble. It is sold in the United States, Canada, and Mexico. Secret was launched as the first female deodorant in 1956, after more than 10 years of research that began in 1945. Secret is the only female brand antiperspirant/deodorant in Procter & Gamble’s portfolio of products, which includes male brands Gillette and Old Spice.

There are currently more than 55 different antiperspirant/deodorant products sold under the Secret brand. Products are produced by company plants in Greensboro, NC and in Mexico City, Mexico, which are then distributed to retailers. Secret products are sold in a variety of channels, including supermarkets, drug stores and mass merchandisers. They are also available through various online retailers.

History

Procter & Gamble began research on the product that would be Secret’s first in 1945. In 1956, Secret was introduced as a cream that was applied with fingers to the underarm area for underarm odor control. It was the first antiperspirant/deodorant product made for, and marketed to, women. In 1958, Secret introduced a roll-on product, with a spray following in 1964. The solid round stick version was launched in 1978.

Secret (Russian band)

Secret (Russian: Секрет) was a Soviet Russian rock and roll band founded in 1982 in Leningrad. The band's musical style and image drawn a heavy inspiration from 1950's and 1960's western music, The Beatles in particular. The band's name was inspired by the Beatles song 'Do You Want to Know a Secret?'. Secret called themselves a "Beat Quartet" and were a part of Soviet rock and roll revival of 1980's, along with Bravo.

The original line-up lasted until 1990, when frontman Maxim Leonidov emigrated to Israel. The band continued with different line-ups without great success. Since 1997 the original line-up has occasionally performed together including for anniversary shows in 2003 and 2007.

Many Secret hits of the 1980s still receive a lot of airplay on Russian FM stations.

Original members

*-algebra

In mathematics, and more specifically in abstract algebra, a *-algebra (or involutive algebra) is a mathematical structure consisting of two involutive rings R and A, where R is commutative and A has the structure of an associative algebra over R. Involutive algebras generalize the idea of a number system equipped with conjugation, for example the complex numbers and complex conjugation, matrices over the complex numbers and conjugate transpose, and linear operators over a Hilbert space and Hermitian adjoints.

Terminology

*-ring

In mathematics, a *-ring is a ring with a map * : A → A that is an antiautomorphism and an involution.

More precisely, * is required to satisfy the following properties:

for all x, y in A.

This is also called an involutive ring, involutory ring, and ring with involution. Note that the third axiom is actually redundant, because the second and fourth axioms imply 1* is also a multiplicative identity, and identities are unique.

Ringtone

A ringtone or ring tone is the sound made by a telephone to indicate an incoming call or text message. Not literally a tone nor an actual (bell-like) ring any more, the term is most often used today to refer to customizable sounds used on mobile phones.

Background

A phone “rings” when its network indicates an incoming call and the phone thus alerts the recipient. For landline telephones, the call signal can be an electric current generated by the switch or exchange to which the telephone is connected, which originally drove an electric bell. For mobile phones, the network sends the phone a message indicating an incoming call. The sound the caller hears is called the ringback tone, which is not necessarily directly related.

The electromagnetic bell system is still in widespread use. The ringing signal sent to a customer's telephone is 90 volts AC at a frequency of 20 hertz in North America. In Europe it is around 60-90 volts AC at a frequency of 25 hertz. Some non-Bell Company system party lines in the US used multiple frequencies (20/30/40 Hz, 22/33/44 Hz, etc.) to allow "selective" ringing.

Sigma-ring

In mathematics, a nonempty collection of sets is called a σ-ring (pronounced sigma-ring) if it is closed under countable union and relative complementation.

Formal definition

Let 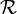be a nonempty collection of sets. Then 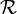is a σ-ring if:

if for all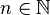

if

Properties

From these two properties we immediately see that

This is simply because .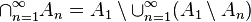

Similar concepts

If the first property is weakened to closure under finite union (i.e., whenever ) but not countable union, then 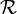is a ring but not a σ-ring.

Uses

σ-rings can be used instead of σ-fields (σ-algebras) in the development of measure and integration theory, if one does not wish to require that the universal set be measurable. Every σ-field is also a σ-ring, but a σ-ring need not be a σ-field.

A σ-ring 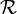that is a collection of subsets of 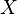induces a σ-field for 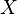. Define to be the collection of all subsets of 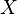that are elements of 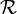or whose complements are elements of 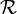. Then is a σ-field over the set 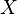. In fact is the minimal σ-field containing 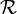since it must be contained in every σ-field containing .

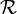Notification

Notification may refer to:

See also