- published: 13 Jan 2010
- views: 1109756
-
remove the playlistMagic Square
- remove the playlistMagic Square
- published: 18 Feb 2013
- views: 276084
- published: 21 Feb 2012
- views: 116297
- published: 08 Nov 2015
- views: 7538
- published: 07 Aug 2009
- views: 119192
- published: 18 Jan 2010
- views: 84941
- published: 20 Feb 2013
- views: 59817
- published: 01 Sep 2012
- views: 91452
- published: 23 Nov 2013
- views: 7636
- published: 24 Sep 2014
- views: 9305

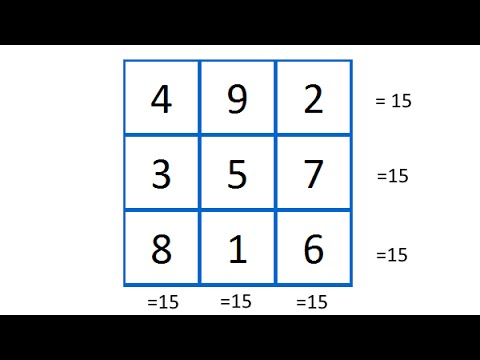
In recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2. The term "magic square" is also sometimes used to refer to any of various types of word square.
Normal magic squares exist for all orders n ≥ 1 except n = 2, although the case n = 1 is trivial, consisting of a single cell containing the number 1. The smallest nontrivial case, shown below, is of order 3.
The constant sum in every row, column and diagonal is called the magic constant or magic sum, M. The magic constant of a normal magic square depends only on n and has the value
For normal magic squares of order n = 3, 4, 5, ..., the magic constants are:
Magic squares were known to Chinese mathematicians, as early as 650 BCE and Arab mathematicians, possibly as early as the 7th century, when the Arabs conquered northwestern parts of the Indian subcontinent and learned Indian mathematics and astronomy, including other aspects of combinatorial mathematics.[citation needed] The first magic squares of order 5 and 6 appear in an encyclopedia from Baghdad circa 983 CE, the Encyclopedia of the Brethren of Purity (Rasa'il Ihkwan al-Safa); simpler magic squares were known to several earlier Arab mathematicians. Some of these squares were later used in conjunction with magic letters as in (Shams Al-ma'arif) to assist Arab illusionists and magicians.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.

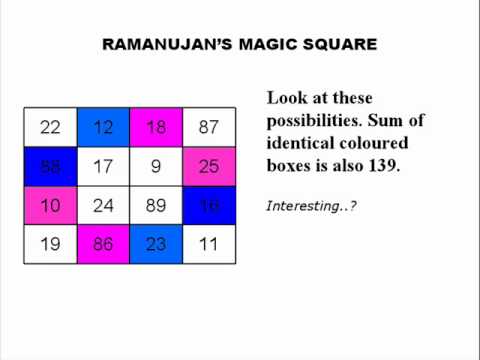
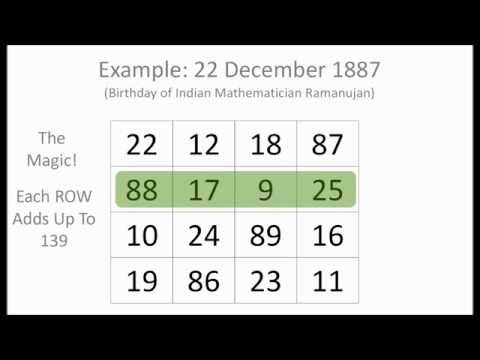
Srīnivāsa Rāmānujan FRS ![]() pronunciation (help·info) (Tamil: ஸ்ரீநிவாச ராமானுஜன்) (22 December 1887 – 26 April 1920) was an Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions. Ramanujan was said to be a natural genius by the English mathematician G.H. Hardy, in the same league as mathematicians like Euler and Gauss.
pronunciation (help·info) (Tamil: ஸ்ரீநிவாச ராமானுஜன்) (22 December 1887 – 26 April 1920) was an Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions. Ramanujan was said to be a natural genius by the English mathematician G.H. Hardy, in the same league as mathematicians like Euler and Gauss.
Born in a poor Brahmin family, Ramanujan's introduction to formal mathematics began at age 10. He demonstrated a natural ability, and was given books on advanced trigonometry written by S. L. Loney that he mastered them by age 12, and even discovered theorems of his own, including independently re-discovering Euler's identity. He demonstrated unusual mathematical skills at school, winning accolades and awards. By 17, Ramanujan conducted his own mathematical research on Bernoulli numbers and the Euler–Mascheroni constant. Ramanujan received a scholarship to study at Government College in Kumbakonam, but lost it when he failed his non-mathematical coursework. He joined another college to pursue independent mathematical research, working as a clerk in the Accountant-General's office at the Madras Port Trust Office to support himself. In 1912–1913, he sent samples of his theorems to three academics at the University of Cambridge. G. H. Hardy, recognizing the brilliance of his work, invited Ramanujan to visit and work with him at Cambridge. He became a Fellow of the Royal Society and a Fellow of Trinity College, Cambridge, dying of illness, malnutrition and possibly liver infection in 1920 at the age of 32.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
Penn & Teller (Penn Jillette and Teller) are American illusionists and entertainers who have performed together since the late 1970s, and are known for their numerous stage and television shows. Their current Las Vegas show is an amalgam of illusion and comedy. Penn Jillette is a raconteur; Teller generally does not speak while performing, although his voice can occasionally be heard during their performance. They specialize in gory tricks, exposing frauds, and performing clever pranks. More recently they have become associated with atheism, scientific skepticism, and libertarianism, particularly through their television show Penn & Teller: Bullshit!.
Penn Jillette and Teller were introduced to one another by Weir Chrisimer, and they performed their first show together at the Minnesota Renaissance Festival on 19 August 1975. From the late 1970s through 1981, Penn, Teller, and Chrisimer performed as a trio called "The Asparagus Valley Cultural Society" which played in San Francisco at the Phoenix Theater. This act was sillier and less "edgy" than today's Penn & Teller act.[citation needed] Chrisimer helped to develop some bits that continued, most notably Teller's "Shadows" trick, which involves a single red rose.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...

-
 5:59
5:59Magic Square Tutorial
Magic Square TutorialMagic Square Tutorial
Amazing mathematical "magic" square. A spectator names any two digit number between 22-99 and after you fill in the 16 boxes there will be 28 possible combinations where the boxes will add up to the spectators number. Credit for teaching me this goes to SingingBanana. Please SUBSCRIBE to http://www.youtube.com/singingbanana -
 2:03
2:033x3 Magic Square
3x3 Magic Square3x3 Magic Square
This video will show you how to make a 3x3 magic square using the basic up-one, right-one method. -
 4:00
4:00The Magic Square Performed by Ben Mack
The Magic Square Performed by Ben MackThe Magic Square Performed by Ben Mack
Ben Mack demonstrates the magic square. -
 4:09
4:09Special Magic Square - Numberphile
Special Magic Square - NumberphileSpecial Magic Square - Numberphile
Magic squares are pretty interesting for Numberphiles any day of the week - but Roger shows us one with extra special "powers". Professor Roger Bowley works at the University of Nottingham. His drawing of the magic square can be seen at: http://www.flickr.com/photos/numberphile/6477417809 Website: http://www.numberphile.com/ Numberphile on Facebook: http://www.facebook.com/numberphile Numberphile tweets: https://twitter.com/numberphile About brown paper: http://periodicvideos.blogspot.com/2012/02/brown-paper-question.html Videos by Brady Haran Brady's other channels include: http://www.youtube.com/periodicvideos (Chemistry stuff) http://www.youtube.com/sixtysymbols (Physics and astronomy) http://www.youtube.com/DeepSkyVideos (Space stuff) http://www.youtube.com/nottinghamscience (Science and behind the scenes) http://www.youtube.com/foodskey (Food science) http://www.youtube.com/BackstageScience (Big science facilities) http://www.youtube.com/favscientist (Favourite scientists) http://www.youtube.com/bibledex (Academic look at the Bible) http://www.youtube.com/wordsoftheworld (Modern language and culture) -
 9:05
9:05SOLVE The 3x3 Magic Square Completely
SOLVE The 3x3 Magic Square CompletelySOLVE The 3x3 Magic Square Completely
A magic square has every row, column, and diagonal sum to the same number. How many magic squares are there using the numbers 1 to 9? This video shows you all the possibilities and proves there are no others, leading to the surprising result the 3x3 magic square is essentially unique, up to symmetries of a square. Blog post http://wp.me/p6aMk-4nC Relevant Math Stack Exchange http://math.stackexchange.com/questions/636633/how-to-prove-that-a-3-times-3-magic-square-must-have-5-in-its-middle-cell If you like my videos, you can support me at Patreon: http://www.patreon.com/mindyourdecisions Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you. My Blog: http://mindyourdecisions.com/blog/ Twitter: http://twitter.com/preshtalwalkar Facebook: https://www.facebook.com/pages/Mind-Your-Decisions/168446714965 Google+: https://plus.google.com/108336608566588374147/posts Pinterest: https://www.pinterest.com/preshtalwalkar/ Tumblr: http://preshtalwalkar.tumblr.com/ Instagram: https://instagram.com/preshtalwalkar/ Patreon: http://www.patreon.com/mindyourdecisions Newsletter (sent about 2 times a year): http://eepurl.com/KvS0r My Books Here's a listing of all my books http://goo.gl/BDlEkB Here's a more detailed description of each book... "The Joy of Game Theory" shows how you can use math to out-think your competition. (rated 4.2/5 stars on 17 reviews) http://amzn.to/1uQvA20 "Math Puzzles Volume 1" features classic brain teasers and riddles with complete solutions for problems in counting, geometry, probability, and game theory. Volume 1 is rated 4.6/5 stars on 9 reviews. http://amzn.to/1GhUUSH "Math Puzzles Volume 2" is a sequel book with more great problems. http://amzn.to/1NKbyCs "Math Puzzles Volume 3" is the third in the series. http://amzn.to/1NKbGlp "40 Paradoxes in Logic, Probability, and Game Theory" contains thought-provoking and counter-intuitive results. (rated 4.9/5 stars on 7 reviews) http://amzn.to/1LOCI4U "The Best Mental Math Tricks" teaches how you can look like a math genius by solving problems in your head http://amzn.to/18maAdo "Multiply Numbers By Drawing Lines" This book is a reference guide for my video that has over 1 million views on a geometric method to multiply numbers. http://amzn.to/XRm7M4 -
 4:47
4:47Magic square (4×4) BEST VIDEO TO UNDERSTAND
Magic square (4×4) BEST VIDEO TO UNDERSTANDMagic square (4×4) BEST VIDEO TO UNDERSTAND
-
 3:39
3:39Magic Square - Sixty Symbols
Magic Square - Sixty SymbolsMagic Square - Sixty Symbols
Bit of Da Vinci Code moment here as Professor Eaves fuses his love of mathematical games and a famous piece of art. More videos at http://www.sixtysymbols.com/ -
 5:00
5:00Response: Magic Square Tutorial
Response: Magic Square TutorialResponse: Magic Square Tutorial
A response to mismag822's Magic Square Tutorial http://www.youtube.com/watch?v=NVx9xfOl10o With no explanation, making a 5x5 magic square - using a completely different method. I should probably plug my website thing more. Follow me in your favourite flavour: http://singingbanana.com -
 3:44
3:445x5 Magic Square
5x5 Magic Square5x5 Magic Square
This video shows how to construct a 5 x 5 magic square using the basic up-one right-one method. -
 1:41
1:41SRINIVASA RAMANUJAN'S MAGIC SQUARE II
SRINIVASA RAMANUJAN'S MAGIC SQUARE IISRINIVASA RAMANUJAN'S MAGIC SQUARE II
SRINIVASA RAMANUJAN'S MAGIC SQUARE II This square looks like any other normal magic square. But this is formed by great mathematician of our country, India -- Srinivasa Ramanujan. You can also view our other pregnancy, maternity, mother care, pre & post natal information, sex education, health benefits & home made beauty tips videos to get solution to your all health & beauty related problems naturally. SUBSCRIBE OUR CHANNEL FOR REGULAR UPDATES: http://www.youtube.com/subscription_center?add_user=f3infojunction Like us on Facebook: http://www.facebook.com/FirstFrameFilms Follow us on Twitter: http://www.twitter.com/FirstFrameFilms You can also share this video on Whatsapp too. Please visit our other channels as they are fully accomplished to meet your queries in relevance with all types of information. These videos will be about beauty tips, health tips, cooking tips, pregnancy information, comedy and many more entertaining & informative stuff by our talented and experts anchors. Click on the link below to get lots of beauty tips by a famous Movie & TV actress Roma https://www.youtube.com/playlist?list=PLXku-YdJ9NKiEqqpKZd29UXIw-GstuZ0L&action;_edit=1 Many more beauty tips by a young, talented & beautiful TV actress Ms. Jyotika Sharma https://www.youtube.com/playlist?list=PLXku-YdJ9NKjN4SLkZsz0F1_hzY3yWQD1 Click on the link below to get more than 400 home remedies to cure yourself and your near & dear ones lives naturally and without any side effects by Multi talented & expert anchor Mr. Piyush Shrivastava https://www.youtube.com/f3healthcare Click on the link below to have a stress free and healthy life style by the group of very talented, expertise & famous Yoga instructors. https://www.youtube.com/f3yogameditation For all the bachelors out there, who lives alone without family. F3 is here to solve all your kitchen queries. Click on the link below to have more than 300 cooking recipes in various cuisines to meet your appetite level in a healthier manner by our very own talented Chef Mr. Piyush Shrivastava https://www.youtube.com/f3bachelorscooking Click on the link below to have a solution to all your queries related to beauty and kitchen by very famous & beautiful TV & Movie actress Ms. Priyanka Saini https://www.youtube.com/f3priyankakitchen&beautytips; Click on the link below to get various types of delicious, tempting, quick to make cooking recipes that includes solutions for your all the cooking related queries from our multiple & multi talented anchors. https://www.youtube.com/f3recipes click on the link below to have solution for all the queries & remarkable information related to your kids behavioural problems, beauty tips & lot of informative videos related to your internal and external health and many more. https://www.youtube.com/f3infojunction Click on the link below and get entered into the lovely world of kids loaded with melodious rhymes & moral stories. https://www.youtube.com/playlist?action_edit=1&list;=PLkw5AtVqSy1Si3R6L7UQ0E1_82DW3nIZP Click on the link given below to get more delicious & mouth watering and instant recipes. https://www.youtube.com/playlist?list=PLkw5AtVqSy1QqIiArE3QokUN6mbV5Jodl&action;_edit=1. -
 8:19
8:19Magic Square Concept (Amazing)!!
Magic Square Concept (Amazing)!!Magic Square Concept (Amazing)!!
How to distribute numbers from 1-25 in a grid of 5*5 so that total of each row and each column is same!! -
 1:15
1:15Make A 4x4 Magic Square From Your Birthday!
Make A 4x4 Magic Square From Your Birthday!Make A 4x4 Magic Square From Your Birthday!
I have made a website so you can automatically generate your 4x4 birthday magic square: http://mindyourdecisions.com/MagicSquare.html A birthday magic square has all rows, columns, diagonals, and most 2x2 blocks add to the same number. The song in the video is Jingle Punks "Sound Off" downloaded from YouTube's Audio Library. If you like my videos, you can support me at Patreon: http://www.patreon.com/mindyourdecisions Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you. My Blog: http://mindyourdecisions.com/blog/ Twitter: http://twitter.com/preshtalwalkar Facebook: https://www.facebook.com/pages/Mind-Your-Decisions/168446714965 Google+: https://plus.google.com/108336608566588374147/posts Pinterest: https://www.pinterest.com/preshtalwalkar/ Tumblr: http://preshtalwalkar.tumblr.com/ Instagram: https://instagram.com/preshtalwalkar/ Patreon: http://www.patreon.com/mindyourdecisions Newsletter (sent about 2 times a year): http://eepurl.com/KvS0r My Books Here's a listing of all my books http://goo.gl/BDlEkB Here's a more detailed description of each book... "The Joy of Game Theory" shows how you can use math to out-think your competition. (rated 4.2/5 stars on 17 reviews) http://amzn.to/1uQvA20 "Math Puzzles Volume 1" features classic brain teasers and riddles with complete solutions for problems in counting, geometry, probability, and game theory. Volume 1 is rated 4.6/5 stars on 9 reviews. http://amzn.to/1GhUUSH "Math Puzzles Volume 2" is a sequel book with more great problems. http://amzn.to/1NKbyCs "Math Puzzles Volume 3" is the third in the series. http://amzn.to/1NKbGlp "40 Paradoxes in Logic, Probability, and Game Theory" contains thought-provoking and counter-intuitive results. (rated 4.9/5 stars on 7 reviews) http://amzn.to/1LOCI4U "The Best Mental Math Tricks" teaches how you can look like a math genius by solving problems in your head http://amzn.to/18maAdo "Multiply Numbers By Drawing Lines" This book is a reference guide for my video that has over 1 million views on a geometric method to multiply numbers. http://amzn.to/XRm7M4 -
 2:50
2:50How to solve a magic square in 3 minutes
How to solve a magic square in 3 minutesHow to solve a magic square in 3 minutes
This quick tutorial shows you how to solve magic squares of all sizes. -
 6:03
6:03As Seen on Penn & Teller Fool Us // Amazing Allison's Magic Square
As Seen on Penn & Teller Fool Us // Amazing Allison's Magic SquareAs Seen on Penn & Teller Fool Us // Amazing Allison's Magic Square
Amazing Allison performs the Magic Square
- 650 BC
- Ahmad al-Buni
- Al-Buni
- Albrecht Dürer
- Ali Skalli
- Amulet
- Ancient China
- Angel
- Antimagic square
- Arab
- Arabic language
- Arithmetic sequence
- Arthur Cayley
- Astrology
- Athanasius Kircher
- Baghdad
- Barcelona
- Barink
- Beirut
- Benjamin Franklin
- Bimagic square
- Buzjani
- Chen prime
- Chess
- Chinese literature
- Chinese year
- Chronos
- Cliff Pickover
- Complex numbers
- Counter-reformation
- Dan Brown
- Demon
- Dodecahedron
- Donald Morris
- Doubly even
- Egypt
- Eight queens puzzle
- Eric W. Weisstein
- Euler
- Franklin squares
- Genetic algorithms
- Green–Tao theorem
- Grimoire
- Group theory
- Hebrew
- Hermeticism
- Heterosquare
- Idries Shah
- Illusionists
- India
- Indian astronomy
- Indian mathematics
- Indian subcontinent
- Integer
- Invocation
- Islamic Golden Age
- Islamic mathematics
- Jain
- Jesus
- John Horton Conway
- John R. Hendricks
- Josep Subirachs
- Jupiter (astrology)
- Kamea
- Key of Solomon
- Khajuraho
- Kronecker product
- Latin square
- Lee Sallows
- Lo Shu
- Lo Shu Square
- Luca Pacioli
- Magic (paranormal)
- Magic constant
- Magic cube
- Magic cube classes
- Magic hexagon
- Magic hypercube
- Magic series
- Magic square
- Magic star
- Magic tesseract
- Magic triangle
- Manuel Moschopoulos
- Mars (astrology)
- Marsilio Ficino
- MathWorld
- Matrix (mathematics)
- Medjig
- Melencolia I
- Mercury (astrology)
- Moon (astrology)
- Multimagic square
- Mystic square
- Nevill Drury
- OEIS A006003
- OEIS A006052
- Oswald Jacoby
- Panmagic square
- Parshvanath
- Pico della Mirandola
- Prime number
- Queen (chess)
- Room square
- Rudolf Ondrejka
- Sagrada Família
- Saturn
- Saturn (astrology)
- Shams Al-ma'arif
- Shams al-Ma'arif
- Siamese method
- Sigil (magic)
- Solar term
- Spirit
- Square (geometry)
- Sudoku
- Sun (astrology)
- The Lost Symbol
- The Observer
- Trimagic square
- Turtle
- Vedic square
- Venus (astrology)
- Wikisource
- Willem Barink
- Word square
- Yang Hui
- Yuan Dynasty
-

Magic Square Tutorial
Amazing mathematical "magic" square. A spectator names any two digit number between 22-99 and after you fill in the 16 boxes there will be 28 possible combinations where the boxes will add up to the spectators number. Credit for teaching me this goes to SingingBanana. Please SUBSCRIBE to http://www.youtube.com/singingbanana -

3x3 Magic Square
This video will show you how to make a 3x3 magic square using the basic up-one, right-one method. -

The Magic Square Performed by Ben Mack
Ben Mack demonstrates the magic square. -

Special Magic Square - Numberphile
Magic squares are pretty interesting for Numberphiles any day of the week - but Roger shows us one with extra special "powers". Professor Roger Bowley works at the University of Nottingham. His drawing of the magic square can be seen at: http://www.flickr.com/photos/numberphile/6477417809 Website: http://www.numberphile.com/ Numberphile on Facebook: http://www.facebook.com/numberphile Numberphile tweets: https://twitter.com/numberphile About brown paper: http://periodicvideos.blogspot.com/2012/02/brown-paper-question.html Videos by Brady Haran Brady's other channels include: http://www.youtube.com/periodicvideos (Chemistry stuff) http://www.youtube.com/sixtysymbols (Physics and astronomy) http://www.youtube.com/DeepSkyVideos (Space stuff) http://www.youtube.com/nottinghamscience (Scie... -

SOLVE The 3x3 Magic Square Completely
A magic square has every row, column, and diagonal sum to the same number. How many magic squares are there using the numbers 1 to 9? This video shows you all the possibilities and proves there are no others, leading to the surprising result the 3x3 magic square is essentially unique, up to symmetries of a square. Blog post http://wp.me/p6aMk-4nC Relevant Math Stack Exchange http://math.stackexchange.com/questions/636633/how-to-prove-that-a-3-times-3-magic-square-must-have-5-in-its-middle-cell If you like my videos, you can support me at Patreon: http://www.patreon.com/mindyourdecisions Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you. My Blog: http://mindyourdecisions.com/blog/ Twitt... -

Magic square (4×4) BEST VIDEO TO UNDERSTAND
-

Magic Square - Sixty Symbols
Bit of Da Vinci Code moment here as Professor Eaves fuses his love of mathematical games and a famous piece of art. More videos at http://www.sixtysymbols.com/ -

Response: Magic Square Tutorial
A response to mismag822's Magic Square Tutorial http://www.youtube.com/watch?v=NVx9xfOl10o With no explanation, making a 5x5 magic square - using a completely different method. I should probably plug my website thing more. Follow me in your favourite flavour: http://singingbanana.com -

5x5 Magic Square
This video shows how to construct a 5 x 5 magic square using the basic up-one right-one method. -

SRINIVASA RAMANUJAN'S MAGIC SQUARE II
SRINIVASA RAMANUJAN'S MAGIC SQUARE II This square looks like any other normal magic square. But this is formed by great mathematician of our country, India -- Srinivasa Ramanujan. You can also view our other pregnancy, maternity, mother care, pre & post natal information, sex education, health benefits & home made beauty tips videos to get solution to your all health & beauty related problems naturally. SUBSCRIBE OUR CHANNEL FOR REGULAR UPDATES: http://www.youtube.com/subscription_center?add_user=f3infojunction Like us on Facebook: http://www.facebook.com/FirstFrameFilms Follow us on Twitter: http://www.twitter.com/FirstFrameFilms You can also share this video on Whatsapp too. Please visit our other channels as they are fully accomplished to meet your queries in relevance with all... -

Magic Square Concept (Amazing)!!
How to distribute numbers from 1-25 in a grid of 5*5 so that total of each row and each column is same!! -

Make A 4x4 Magic Square From Your Birthday!
I have made a website so you can automatically generate your 4x4 birthday magic square: http://mindyourdecisions.com/MagicSquare.html A birthday magic square has all rows, columns, diagonals, and most 2x2 blocks add to the same number. The song in the video is Jingle Punks "Sound Off" downloaded from YouTube's Audio Library. If you like my videos, you can support me at Patreon: http://www.patreon.com/mindyourdecisions Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you. My Blog: http://mindyourdecisions.com/blog/ Twitter: http://twitter.com/preshtalwalkar Facebook: https://www.facebook.com/pages/Mind-Your-Decisions/168446714965 Google+: https://plus.google.com/108336608566588374147/posts ... -

How to solve a magic square in 3 minutes
This quick tutorial shows you how to solve magic squares of all sizes. -

As Seen on Penn & Teller Fool Us // Amazing Allison's Magic Square
Amazing Allison performs the Magic Square -

Part 2 - 666 Magic Square of the Sun (Revelation 13 M)
Most people, even Hollywood knows that the number of the Beast is "666". But few have ever attempted to understand the meaning of this number, let alone factor it out. When doing so, we begin discover to that 666 is an astronomical number connected to the movements of the sun and may even help us better understand the calendar of the end times. By Pastor Ben Heath Visit us our website: http://www.ChristianOvercomers.com Connect on Facebook: https://www.facebook.com/groups/christianovercomers/ Donate: http://christianovercomers.com/blog/donations-page/ Do you have a Bible Question? http://christianovercomers.com/blog/forums/forum/questions-for-pastor-ben-2/ -

Magic Square Quilt Tutorial Using Pre-cut Fabrics
http://missouriquiltco.com -- Jenny Doan shows demonstrates how to make a Magic Square Quilt using layer cakes (or a smaller version using turnovers and jelly rolls). She demonstrates using Lemon Tree by Kanvas and My True Love Gave to Me by Erin Mcallister (both by Benartex), but you can use the precuts of any other line. To get the materials needed to do this project, follow the links in the description below. Lemon Tree Fabric by Benartex http://www.missouriquiltco.com/shop/browse?q=lemon+tree Layer Cakes - Click below to see the best selection of layer cakes on the net! http://www.missouriquiltco.com/shop/browse/14 Turnovers http://www.missouriquiltco.com/shop/browse/16 Jelly Rolls http://www.missouriquiltco.com/shop/browse/13 Notions - all the everyday tools you'll need to quil... -

The SATOR ROTAS Magic Square
Found buried in the ruins of Pompeii is a bit of graffiti with some magic to it. In this square, you can read forwards, backwards, up, or down, and still get the same message. But along with that is a hidden message of Christianity. -

How To Make 3x3 And 9x9 Magic Squares - Ancient Chinese Algorithm (Lo Shu Square)
Magic squares are arrangements of numbers where every row, column, and diagonal adds up to the same number. The ancient Chinese developed a geometric method to create 3x3 magic squares. Remarkably, they generalized the method to create a 9x9 magic square which is quite the feat! The Lo Shu Method From "The Evolution of Mathematics in Ancient China", Frank Swetz, Jan 1979. Appears in "Sherlock Holmes in Babylon." http://amzn.to/1c2QBSm Lo Shu Square courtesy Wikipedia http://en.wikipedia.org/wiki/File:Lo_Shu_3x3_magic_square.svg *Thanks to Patrons* Kyle Alberto Nishikawa If you like my videos, you can support me at Patreon: http://www.patreon.com/mindyourdecisions Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method ... -

Masonic secrets: Magic square - Union Jack - Creation Window - Crypt
A wander through Sydney's Hyde Park and St James' Church. -

-

Magic Square of RAMANUJAN
22nd December has been declared as the NATIONAL MATHEMATICS DAY. It is the birthday India's great maths hero Srinivasa Ramanujan. -

"The Lost Symbol" - Magic Squares and the Masonic Cipher
December 2, 2009 Dan Brown? The Lost Symbol? Masonic cipher? Albrecht Durers magic square? If you know about these things AND you can decipher the message below, then dont bother coming because you know as much as I do. If you dont know about them OR you cant decipher the message below, then by all means come and hear my presentation. Yes, we do have pizza. Ed Brumgnach http://www.qcc.cuny.edu/ecet/magicSquares.asp -

THE SQUARE (T-SQUARE) - IT'S MAGIC
LIVE in Yoyogi-park. Tokyo, Japan (1987 spring) Takeshi Ito (sax) Masahiro Ando (g) Hirotaka Izumi (key) Hiroyuki Noritake (d) Mitsuru suto (b)
Magic Square Tutorial
- Order: Reorder
- Duration: 5:59
- Updated: 13 Jan 2010
- views: 1109756
- published: 13 Jan 2010
- views: 1109756
3x3 Magic Square
- Order: Reorder
- Duration: 2:03
- Updated: 18 Feb 2013
- views: 276084
- published: 18 Feb 2013
- views: 276084
The Magic Square Performed by Ben Mack
- Order: Reorder
- Duration: 4:00
- Updated: 12 Mar 2009
- views: 77698
Special Magic Square - Numberphile
- Order: Reorder
- Duration: 4:09
- Updated: 21 Feb 2012
- views: 116297
- published: 21 Feb 2012
- views: 116297
SOLVE The 3x3 Magic Square Completely
- Order: Reorder
- Duration: 9:05
- Updated: 08 Nov 2015
- views: 7538
- published: 08 Nov 2015
- views: 7538
Magic square (4×4) BEST VIDEO TO UNDERSTAND
- Order: Reorder
- Duration: 4:47
- Updated: 25 Aug 2013
- views: 31702
- published: 25 Aug 2013
- views: 31702
Magic Square - Sixty Symbols
- Order: Reorder
- Duration: 3:39
- Updated: 07 Aug 2009
- views: 119192
- published: 07 Aug 2009
- views: 119192
Response: Magic Square Tutorial
- Order: Reorder
- Duration: 5:00
- Updated: 18 Jan 2010
- views: 84941
- published: 18 Jan 2010
- views: 84941
5x5 Magic Square
- Order: Reorder
- Duration: 3:44
- Updated: 20 Feb 2013
- views: 59817
- published: 20 Feb 2013
- views: 59817
SRINIVASA RAMANUJAN'S MAGIC SQUARE II
- Order: Reorder
- Duration: 1:41
- Updated: 01 Sep 2012
- views: 91452
- published: 01 Sep 2012
- views: 91452
Magic Square Concept (Amazing)!!
- Order: Reorder
- Duration: 8:19
- Updated: 23 Nov 2013
- views: 7636
- published: 23 Nov 2013
- views: 7636
Make A 4x4 Magic Square From Your Birthday!
- Order: Reorder
- Duration: 1:15
- Updated: 24 Sep 2014
- views: 9305
- published: 24 Sep 2014
- views: 9305
How to solve a magic square in 3 minutes
- Order: Reorder
- Duration: 2:50
- Updated: 01 Feb 2014
- views: 15396
- published: 01 Feb 2014
- views: 15396
As Seen on Penn & Teller Fool Us // Amazing Allison's Magic Square
- Order: Reorder
- Duration: 6:03
- Updated: 06 Apr 2015
- views: 3257
Part 2 - 666 Magic Square of the Sun (Revelation 13 M)
- Order: Reorder
- Duration: 54:07
- Updated: 26 Nov 2014
- views: 3720
- published: 26 Nov 2014
- views: 3720
Magic Square Quilt Tutorial Using Pre-cut Fabrics
- Order: Reorder
- Duration: 11:13
- Updated: 04 May 2012
- views: 386413
- published: 04 May 2012
- views: 386413
The SATOR ROTAS Magic Square
- Order: Reorder
- Duration: 4:30
- Updated: 09 Nov 2015
- views: 6922
- published: 09 Nov 2015
- views: 6922
How To Make 3x3 And 9x9 Magic Squares - Ancient Chinese Algorithm (Lo Shu Square)
- Order: Reorder
- Duration: 9:10
- Updated: 06 May 2015
- views: 18699
- published: 06 May 2015
- views: 18699
Masonic secrets: Magic square - Union Jack - Creation Window - Crypt
- Order: Reorder
- Duration: 24:08
- Updated: 13 Jul 2013
- views: 4321
Magic Square of RAMANUJAN
- Order: Reorder
- Duration: 1:25
- Updated: 22 Dec 2012
- views: 11636
- published: 22 Dec 2012
- views: 11636
"The Lost Symbol" - Magic Squares and the Masonic Cipher
- Order: Reorder
- Duration: 43:15
- Updated: 16 Dec 2009
- views: 506403
- published: 16 Dec 2009
- views: 506403
THE SQUARE (T-SQUARE) - IT'S MAGIC
- Order: Reorder
- Duration: 5:56
- Updated: 09 Apr 2007
- views: 229513
- published: 09 Apr 2007
- views: 229513
- Playlist
- Chat
- Playlist
- Chat

Magic Square Tutorial
- Report rights infringement
- published: 13 Jan 2010
- views: 1109756

3x3 Magic Square
- Report rights infringement
- published: 18 Feb 2013
- views: 276084

The Magic Square Performed by Ben Mack
- Report rights infringement
- published: 12 Mar 2009
- views: 77698

Special Magic Square - Numberphile
- Report rights infringement
- published: 21 Feb 2012
- views: 116297

SOLVE The 3x3 Magic Square Completely
- Report rights infringement
- published: 08 Nov 2015
- views: 7538

Magic square (4×4) BEST VIDEO TO UNDERSTAND
- Report rights infringement
- published: 25 Aug 2013
- views: 31702

Magic Square - Sixty Symbols
- Report rights infringement
- published: 07 Aug 2009
- views: 119192

Response: Magic Square Tutorial
- Report rights infringement
- published: 18 Jan 2010
- views: 84941

5x5 Magic Square
- Report rights infringement
- published: 20 Feb 2013
- views: 59817

SRINIVASA RAMANUJAN'S MAGIC SQUARE II
- Report rights infringement
- published: 01 Sep 2012
- views: 91452

Magic Square Concept (Amazing)!!
- Report rights infringement
- published: 23 Nov 2013
- views: 7636

Make A 4x4 Magic Square From Your Birthday!
- Report rights infringement
- published: 24 Sep 2014
- views: 9305

How to solve a magic square in 3 minutes
- Report rights infringement
- published: 01 Feb 2014
- views: 15396

As Seen on Penn & Teller Fool Us // Amazing Allison's Magic Square
- Report rights infringement
- published: 06 Apr 2015
- views: 3257
The world looks away as blood flows in Burundi
Edit The Guardian 10 Apr 2016Constant Repairs Required To Keep Iraqi Dam From Collapsing
Edit WorldNews.com 08 Apr 2016Ukrainian Prime Minister Quits, Paving Way for Cabinet Overhaul
Edit Yahoo Daily News 10 Apr 2016Indonesian Singer Dies After Cobra Bites Her Onstage
Edit WorldNews.com 08 Apr 2016Paul Daniels dies: The magician's 12 greatest TV moments
Edit Digital Spy 17 Mar 2016Story of cities #4: Beijing and the earliest planning document in history
Edit The Guardian 17 Mar 2016Sir Peter Maxwell Davies obituary
Edit The Guardian 14 Mar 2016Martin Luther King Jr. Word Games, Jigsaw Puzzles and Quizzes for Kids
Edit About.com 21 Feb 2016WWE 2K16 Confirmed for PC, Comes With All DLC for Free
Edit Gamespot 17 Feb 2016Manning, Magic Square Off in Egg Russian Roulette
Edit NBC News 12 Feb 2016Santa Barbara Pi Day Celebration: Call for Entries (City of Santa Barbara, CA)
Edit Public Technologies 08 Feb 2016Remedies for infertility: how performative rituals entered early medical literature (University of Cambridge)
Edit Public Technologies 25 Jan 2016Free printable math games, math worksheets for hands-on lesson plans
Edit The Examiner 19 Jan 2016Oladipo getting noticed for his off-court work as well
Edit The Oklahoman 15 Jan 2016Orlando Magic touch down in London ahead of NBA showdown with Toronto Raptors
Edit The Daily Mail 13 Jan 2016Spirals within spirals: Vortex Temporum at the Sydney Festival (UNSW - The University of New ...
Edit Public Technologies 12 Jan 2016CBSE schools to celebrate Ramanujan's birth anniversary
Edit The Times of India 15 Dec 2015- 1
- 2
- 3
- 4
- 5
- Next page »







