- published: 09 Apr 2013
- views: 212073
-
remove the playlistWhta Cha Gon Do Family
- remove the playlistWhta Cha Gon Do Family
- published: 23 Jan 2017
- views: 245301
- published: 09 Nov 2014
- views: 64653
- published: 20 Oct 2016
- views: 4020
- published: 08 Nov 2014
- views: 8388
- published: 23 Sep 2015
- views: 55380
- published: 17 Oct 2021
- views: 15965
- published: 13 Aug 2018
- views: 60
- published: 22 Aug 2016
- views: 143133
- published: 17 Mar 2014
- views: 3568

Tetracontaoctagon
In geometry, a tetracontaoctagon (or tetracontakaioctagon) is a forty-eight-sided polygon or 48-gon. The sum of any tetracontaoctagon's interior angles is 8280 degrees.
Regular tetracontaoctagon
The regular tetracontaoctagon is represented by Schläfli symbol {48} and can also be constructed as a truncated icositetragon, t{24}, or a twice-truncated dodecagon, tt{12}, or a thrice-truncated hexagon, ttt{6}, or a fourfold-truncated triangle, tttt{3}.
One interior angle in a regular tetracontaoctagon is 1721⁄2°, meaning that one exterior angle would be 71⁄2°.
The area of a regular tetracontaoctagon is: (with t = edge length)
The tetracontaoctagon appeared in Archimedes' polygon approximation of pi, along with the hexagon (6-gon), dodecagon (12-gon), icositetragon (24-gon), and enneacontahexagon (96-gon).
Construction
Since 48 = 24 × 3, a regular tetracontaoctagon is constructible using a compass and straightedge. As a truncated icositetragon, it can be constructed by an edge-bisection of a regular icositetragon.

Enneacontagon
In geometry, an enneacontagon or enenecontagon (from Ancient Greek ἑννενήκοντα, ninety) is a ninety-sided polygon or 90-gon. The sum of any enneacontagon's interior angles is 15840 degrees.
A regular enneacontagon is represented by Schläfli symbol {90} and can be constructed as a truncated tetracontapentagon, t{45}, which alternates two types of edges.
Regular enneacontagon properties
One interior angle in a regular enneacontagon is 176°, meaning that one exterior angle would be 4°.
The area of a regular enneacontagon is (with t = edge length)
and its inradius is
The circumradius of a regular enneacontagon is
Since 90 = 2 × 32 × 5, a regular enneacontagon is not constructible using a compass and straightedge, but is constructible if the use of an angle trisector is allowed.
Symmetry
The regular enneacontagon has Dih90dihedral symmetry, order 180, represented by 90 lines of reflection. Dih90 has 11 dihedral subgroups: Dih45, (Dih30, Dih15), (Dih18, Dih9), (Dih10, Dih5), (Dih6, Dih3), and (Dih2, Dih1). And 12 more cyclic symmetries: (Z90, Z45), (Z30, Z15), (Z18, Z9), (Z10, Z5), (Z6, Z3), and (Z2, Z1), with Zn representing π/n radian rotational symmetry.

Triacontagon
In geometry, a triacontagon is a thirty-sided polygon or 30-gon. The sum of any triacontagon's interior angles is 5040 degrees.
Regular triacontagon
The regular triacontagon is a constructible polygon, by an edge-bisection of a regular pentadecagon, and can also be constructed as a truncated pentadecagon, t{15}. A truncated triacontagon, t{30}, is a hexacontagon, {60}.
One interior angle in a regular triacontagon is 168°, meaning that one exterior angle would be 12°. The triacontagon is the largest regular polygon whose interior angle is the sum of the interior angles of smaller polygons: 168° is the sum of the interior angles of the equilateral triangle (60°) and the regular pentagon (108°).
The area of a regular triacontagon is (with t = edge length)
The inradius of a regular triacontagon is
The circumradius of a regular triacontagon is
Construction
As 30 = 2 × 3 × 5, a regular triacontagon is constructible using a compass and straightedge.
Symmetry
The regular triacontagon has Dih30dihedral symmetry, order 60, represented by 30 lines of reflection. Dih30 has 7 dihedral subgroups: Dih15, (Dih10, Dih5), (Dih6, Dih3), and (Dih2, Dih1). It also has eight more cyclic symmetries as subgroups: (Z30, Z15), (Z10, Z5), (Z6, Z3), and (Z2, Z1), with Zn representing π/n radian rotational symmetry.

Family Π
Family Π is a group of New Testament manuscripts. Belonging to the Byzantine text-type, it is one of the textual families of this group. The name of the family, "Π" (pronounced in English as "pie"), is drawn from the symbol used for the Codex Petropolitanus. One of the most distinct of the Byzantine sub-groups, it is very old and the third largest. The oldest Byzantine manuscripts belong to this family.
Hermann von Soden designated this group by the symbol "Ka". According to him, its text is not purely Byzantine.
Codices and manuscripts
Soden included the following in this group of codices: Cyprius (K), Petropolitanus (Π), 72, 114, 116, 178, 265, 389, 1008, 1009, 1079, 1154, 1200, 1219, 1346, and 1398. Lake added to this group of manuscripts: 489, 537, 652, 775, 796, 904, 1478, 1500, 1546, 1561, 1781, 1816. Soden also associated Codex Alexandrinus with this group. Wisse lists about 150 witnesses of the family, but the majority of them belong to this family only in some parts of their text. The Peshitta, in the Gospels, represents this family.
Index set
In mathematics, an index set is a set whose members label (or index) members of another set. For instance, if the elements of a set A may be indexed or labeled by means of a set J, then J is an index set. The indexing consists of a surjective function from J onto A and the indexed collection is typically called an (indexed) family, often written as (Aj)j∈J.
Examples
 , where f : J → S is the particular enumeration of S.
, where f : J → S is the particular enumeration of S. .
.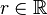 , the indicator function on r is the function
, the indicator function on r is the function  given by
given byThe set of all the 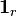 functions is an uncountable set indexed by
functions is an uncountable set indexed by 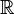 .
.
Other uses
In computational complexity theory and cryptography, an index set is a set for which there exists an algorithm I that can sample the set efficiently; i.e., on input 1n, I can efficiently select a poly(n)-bit long element from the set.
See also
References
Family (Spanish band)
Family was a cult band from Spain in the 1990s. Although initially unsuccessful, Family gradually acquired a fanbase and is now highly recognised in the Spanish underground pop scene. Their only album, Un Soplo en el Corazón has been praised for its poetic lyrics, inspired music and elegant artwork.
Family - Un Soplo en el Corazón (Tracklist)
1. La Noche Inventada (2:24)
2. Nadadora (2:57)
3. Como un Aviador (3:19)
4. En el Rascacielos (2:32)
5. El Bello Verano (2:19)
6. Portugal (2:10)
7. El Buen Vigía (2:05)
8. Viaje a los Sueños Polares (2:53)
9. Al Otro Lado (2:02)
10. Carlos Baila (2:49)
11. Yo TePerdí una Tarde de Abril (3:01)
12. Dame Estrellas O Limones (2:24)
13. El mapa (2:20)
14. Martín se ha ido para siempre (3:09)
CHA
CHA may refer to:
Sports
Places
Science
Surnames
Other
Podcasts:
-

Pharoah - What'cha Gonna Do
Six Foot Giant ©1997 Beatbox Records
published: 09 Apr 2013 -

Wha Cha Gonna Do
Provided to YouTube by Ingrooves Wha Cha Gonna Do · Bushwick Bill Phantom of the Rapra ℗ Rap-A-Lot/SoSouth Music Distribution Released on: 1995-07-11 Writer, Composer: Bryaan Ross Writer, Composer: John Bido Writer, Composer: Mike Dean Auto-generated by YouTube.
published: 23 Jan 2017 -

What 'Cha Gonna Do?
Provided to YouTube by Epic What 'Cha Gonna Do? · Shabba Ranks · Queen Latifah X-Tra Naked ℗ 1992 SONY BMG MUSIC ENTERTAINMENT Released on: 1992-09-05 Associated Performer: Shabba Ranks feat. Queen Latifah Composer, Lyricist: R. Gordon Composer, Lyricist: C. Dillon Background Vocal: Nadine Sutherland Background Vocal: Brian Gold Composer, Lyricist: Erroll Dillon Background Vocal: Dean Fraser Composer, Lyricist: L Shabazz Background Vocal: Cherelle Franklin Composer, Lyricist: D. Owens Composer, Lyricist: P. Rushen Background Vocal: Todd Gold Composer, Lyricist: F. Washington Background Vocal: Katrese Barnes Composer, Lyricist: G. Brown Background Vocal: Milini Khan Background Vocal: Lisa Robinson Composer, Lyricist: R. Mickens Bass, Drums, Keyboards: Danny Browne Composer, Ly...
published: 09 Nov 2014 -

Shabba Ranks - What'Cha Gonna Do ? (Official Video HD)(Ft. Queen Latifah)(Audio HD)
I've Uploaded & Remasterized, Just to Enjoy Better Quality Audio & Video. Follow Us 4 More Music & Remixes: https://soundcloud.com/santash
published: 20 Oct 2016 -

What'cha Gonna Do
Provided to YouTube by Warner Records What'cha Gonna Do · Sheila E Sex Cymbal ℗ 1991 Warner Records Inc. Background Vocals: Angel Rogers Guitar: Bobby Gonzales Background Vocals: Boni Boyer Background Vocals: Brenda Roy Background Vocals: Carl Carwell Additional Keyboards: Carl Wheeler Guitar: Carlos Rios Bass, Piano: Cat Gray Additional Keyboards: Cat Gray Background Vocals: Cat Gray Additional Keyboards: Dan Shea Horn: Daniel Regan Additional Keyboards: David Gamson Bass: Don Boyette Horn: Eddie M. Guitar: Grant Geissman Guitar: J. D. Riley Additional Keyboards: J.P. Charles Percussion: JOHN Santos Horn: Jeff Cressman Bass: Joel Smith Guitar: Jonathan DuBose Percussion: Juan E. Percussion: Karl Perazzo Background Vocals: Karl Perazzo Horn: Larry Williams Background Vocals...
published: 08 Nov 2014 -

What'Cha Gonna Do (About It)
Provided to YouTube by Columbia What'Cha Gonna Do (About It) · New Kids On The Block Hangin' Tough ℗ 1988 Columbia Records, a division of Sony Music Entertainment Released on: 1988-09-02 Unknown, Mixing Engineer, Producer: Maurice Starr Executive Producer: Cecil Holmes Composer, Lyricist: M. Starr Unknown, Mixing Engineer: Hediki Sunada Unknown: Patrick Spencer Unknown, Mixing Engineer: Phil Greene Unknown, Mixing Engineer: Richard Mendelson Unknown: Danny Wood Unknown: Tom Soars Unknown: Normandy Staff Auto-generated by YouTube.
published: 23 Sep 2015 -

How WE keep CARROTS over Winter (+ Carrot cake)
Today we harvested our carrots and stored them for winter. We also make a carrot cake for the autumn season! Carrot cake recipe: 250g Butter 250g Sugar 250g Flour 4 Eggs 100g Walnuts 50g Chocolate 15g Baking Powder 1 Tea Spoons Cinnamon 1 Tea Spoons Clove Powder 1 Tea Spoon Ginger powder 3 Apples 3 Carrots Make sure you subscribe to follow our daily lives in this farm! Hey to everyone!! We are two young adults, Despina 22 and Deivids 23 renovating an old farm house from 1817 in Latvia. Everything in and out of our house has been done by ourselves with no hired help. Soooo far everything is going great and there haven't been any incidents. DIY is going to apply to nearly everything in our house. Our budget is tight and that has made us appreciate every "ugly" part of this house and tur...
published: 17 Oct 2021 -

Vignette 11 01 What 'cha Gonna Do
This vignette was written for the Bellingwood series while I was in the middle of Book 11 - Look Always Forward. The vignettes are very short stories featuring characters other than Polly Giller. Published in the monthly newsletter (sign up at nammynools.com) as well as on my blog, they offer an opportunity to see what is happening in town when Polly isn't around. They're fun to write and are written while I'm in the middle of writing and editing the next book. A new book is published every three months - March 25, June 25, September 25, and December 25. There are more than twenty full length novels, as well as short stories in the Bellingwood series. Find the entire list here: http://nammynools.com/bellingwood-ser... Join us on Facebook: https://www.facebook.com/pollygiller/ Diane
published: 13 Aug 2018 -

Shabba Ranks - What 'Cha Gonna Do?
Shabba Ranks ft. Queen Latifah performing "What 'Cha Gonna Do?". http://vevo.ly/tmv2qJ Best of Shabba Ranks: https://goo.gl/EAdBkz Subscribe here: https://goo.gl/3Te3U7 #ShabbaRanks #WhatChaGonnaDo #Vevo #Pop
published: 22 Aug 2016 -

What Cha Gonna Do - Brian Simpson @ Spaghettini (Smooth Jazz Family)
Here's a clip of Brian Simpson performing with Randy Jacobs, Nate Kearney & Frank Richardson III @ Spaghettini in Seal Beach CA 3-14-14. Enjoy and "Stay Smooooth". https://www.facebook.com/SmoothJazzFamily
published: 17 Mar 2014

Pharoah - What'cha Gonna Do
- Order: Reorder
- Duration: 4:50
- Uploaded Date: 09 Apr 2013
- views: 212073
- published: 09 Apr 2013
- views: 212073

Wha Cha Gonna Do
- Order: Reorder
- Duration: 4:09
- Uploaded Date: 23 Jan 2017
- views: 245301
- published: 23 Jan 2017
- views: 245301

What 'Cha Gonna Do?
- Order: Reorder
- Duration: 3:50
- Uploaded Date: 09 Nov 2014
- views: 64653
- published: 09 Nov 2014
- views: 64653

Shabba Ranks - What'Cha Gonna Do ? (Official Video HD)(Ft. Queen Latifah)(Audio HD)
- Order: Reorder
- Duration: 3:51
- Uploaded Date: 20 Oct 2016
- views: 4020
- published: 20 Oct 2016
- views: 4020

What'cha Gonna Do
- Order: Reorder
- Duration: 4:40
- Uploaded Date: 08 Nov 2014
- views: 8388
- published: 08 Nov 2014
- views: 8388

What'Cha Gonna Do (About It)
- Order: Reorder
- Duration: 3:56
- Uploaded Date: 23 Sep 2015
- views: 55380
- published: 23 Sep 2015
- views: 55380

How WE keep CARROTS over Winter (+ Carrot cake)
- Order: Reorder
- Duration: 19:09
- Uploaded Date: 17 Oct 2021
- views: 15965
- published: 17 Oct 2021
- views: 15965

Vignette 11 01 What 'cha Gonna Do
- Order: Reorder
- Duration: 9:19
- Uploaded Date: 13 Aug 2018
- views: 60
- published: 13 Aug 2018
- views: 60

Shabba Ranks - What 'Cha Gonna Do?
- Order: Reorder
- Duration: 3:36
- Uploaded Date: 22 Aug 2016
- views: 143133
- published: 22 Aug 2016
- views: 143133

What Cha Gonna Do - Brian Simpson @ Spaghettini (Smooth Jazz Family)
- Order: Reorder
- Duration: 6:01
- Uploaded Date: 17 Mar 2014
- views: 3568
- published: 17 Mar 2014
- views: 3568



Pharoah - What'cha Gonna Do
- Report rights infringement
- published: 09 Apr 2013
- views: 212073

Wha Cha Gonna Do
- Report rights infringement
- published: 23 Jan 2017
- views: 245301

What 'Cha Gonna Do?
- Report rights infringement
- published: 09 Nov 2014
- views: 64653

Shabba Ranks - What'Cha Gonna Do ? (Official Video HD)(Ft. Queen Latifah)(Audio HD)
- Report rights infringement
- published: 20 Oct 2016
- views: 4020

What'cha Gonna Do
- Report rights infringement
- published: 08 Nov 2014
- views: 8388

What'Cha Gonna Do (About It)
- Report rights infringement
- published: 23 Sep 2015
- views: 55380

How WE keep CARROTS over Winter (+ Carrot cake)
- Report rights infringement
- published: 17 Oct 2021
- views: 15965

Vignette 11 01 What 'cha Gonna Do
- Report rights infringement
- published: 13 Aug 2018
- views: 60

Shabba Ranks - What 'Cha Gonna Do?
- Report rights infringement
- published: 22 Aug 2016
- views: 143133

What Cha Gonna Do - Brian Simpson @ Spaghettini (Smooth Jazz Family)
- Report rights infringement
- published: 17 Mar 2014
- views: 3568

Tetracontaoctagon
In geometry, a tetracontaoctagon (or tetracontakaioctagon) is a forty-eight-sided polygon or 48-gon. The sum of any tetracontaoctagon's interior angles is 8280 degrees.
Regular tetracontaoctagon
The regular tetracontaoctagon is represented by Schläfli symbol {48} and can also be constructed as a truncated icositetragon, t{24}, or a twice-truncated dodecagon, tt{12}, or a thrice-truncated hexagon, ttt{6}, or a fourfold-truncated triangle, tttt{3}.
One interior angle in a regular tetracontaoctagon is 1721⁄2°, meaning that one exterior angle would be 71⁄2°.
The area of a regular tetracontaoctagon is: (with t = edge length)
The tetracontaoctagon appeared in Archimedes' polygon approximation of pi, along with the hexagon (6-gon), dodecagon (12-gon), icositetragon (24-gon), and enneacontahexagon (96-gon).
Construction
Since 48 = 24 × 3, a regular tetracontaoctagon is constructible using a compass and straightedge. As a truncated icositetragon, it can be constructed by an edge-bisection of a regular icositetragon.
