- published: 28 Jun 2013
- views: 637
-
remove the playlistScalar (physics)
-
remove the playlistLatest Videos
-
remove the playlistLongest Videos
- remove the playlistScalar (physics)
- remove the playlistLatest Videos
- remove the playlistLongest Videos
- published: 11 Jun 2011
- views: 1816716
- published: 20 Sep 2009
- views: 22022
- published: 28 Jun 2011
- views: 55793
- published: 12 Sep 2011
- views: 72415
- published: 10 Aug 2013
- views: 4424
- published: 23 Jan 2011
- views: 129134
- published: 15 Sep 2015
- views: 828
- published: 09 Mar 2014
- views: 1955
- published: 07 Aug 2011
- views: 40352
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations (in Newtonian mechanics), or by Lorentz transformations or space-time translations (in relativity). This is in contrast to a vector. A related concept is a pseudoscalar, which is invariant under proper rotations but (like a pseudovector) flips sign under improper rotations.
A physical quantity is expressed as the product of a numerical value and a physical unit, not merely a number. The quantity does not depend on the unit (i.e for distance, 1 km is the same as 1000 m), although the number depends on the unit. Thus, following the example of distance, the quantity does not depend on the length of the base vectors of the coordinate system. Also, other changes of the coordinate system may affect the formula for computing the scalar (for example, the Euclidean formula for distance in terms of coordinates relies on the basis being orthonormal), but not the scalar itself. In this sense, physical distance deviates from the definition of metric in not being just a real number; however it satisfies all other properties. The same applies for other physical quantities which are not dimensionless. Direction does not apply to scalars; they are specified by magnitude or quantity alone.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...

-
 92:31
92:31New Scalar Model of Physics - Full Version
New Scalar Model of Physics - Full VersionNew Scalar Model of Physics - Full Version
A New Model of Physics that address the anomalies of the Standard Model -
 8:39
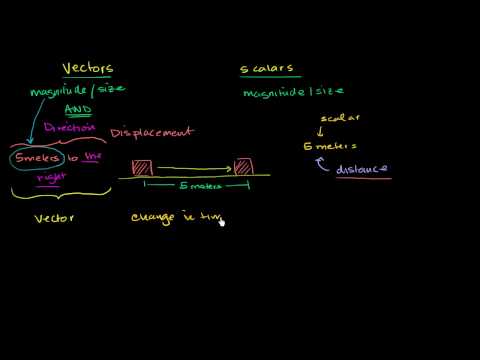
8:39Introduction to Vectors and Scalars
Introduction to Vectors and ScalarsIntroduction to Vectors and Scalars
Distance, displacement, speed and velocity. Difference between vectors and scalars More free lessons at: http://www.khanacademy.org/video?v=ihNZlp7iUHE -
 63:58
63:58Technical proof: scalar waves exist
Technical proof: scalar waves existTechnical proof: scalar waves exist
-
 10:00
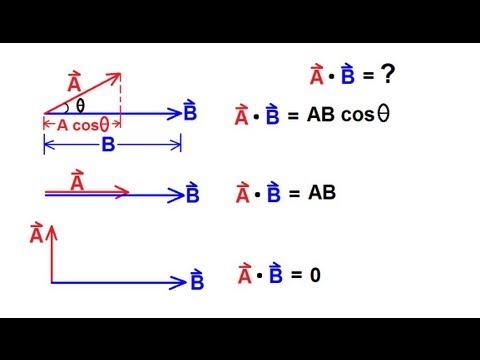
10:00The Scalar Product or Dot Product for Physics
The Scalar Product or Dot Product for PhysicsThe Scalar Product or Dot Product for Physics
An introduction to the scalar product of dot product for AP Physics. -
 15:08
15:08High School Physics: Vectors and Scalars
High School Physics: Vectors and ScalarsHigh School Physics: Vectors and Scalars
In this video Dan Fullerton provides a brief introduction to vectors and scalars for students in high school physics courses including Regents Physics, IB, AP Physics, and others. APlusPhysics.com provides a variety of free educational resources to assist students in finding success in high school physics courses such as Honors Physics, Regents Physics, and AP Physics. Resources include video mini-lessons, online tutorials, help forums, problem sets, downloads, and review books. You may also be interested in related videos in this series: https://www.youtube.com/playlist?list=PLB03A41EA88A8DE65 For more information, check out http://aplusphysics.com, and associated books in the series specific to courses: Regents Physics Essentials: http://aplusphysics.com/regents/ Honors Physics Essentials: http://aplusphysics.com/honors/ AP Physics 1 Essentials: http://aplusphysics.com/ap1/ AP Physics 2 Essentials: http://aplusphysics.com/ap2/ -
 11:00
11:00Physics Motion in plane part 1 (Introduction to Scalar and Vector) CBSE class 11
Physics Motion in plane part 1 (Introduction to Scalar and Vector) CBSE class 11Physics Motion in plane part 1 (Introduction to Scalar and Vector) CBSE class 11
Physics Motion in plane part 1 (Introduction to Scalar and Vector) CBSE class 11 -
 1:25
1:25(7) IGCSE Physics in 60 Seconds - Vector and Scalar Quantities
(7) IGCSE Physics in 60 Seconds - Vector and Scalar Quantities(7) IGCSE Physics in 60 Seconds - Vector and Scalar Quantities
A short and sweet video explaining about Vector and Scalar quantities! Created by a GCSE student, for GCSE students :) Like, Comment, Subscribe if you found this video helpful! Feel free to comment if you have any questions you would like to ask! Check out my blog :) - http://ohigetitnowebz.blogspot.co.uk/ Thanks for watching! - Music from www.freemusicforvideos.com -
 12:34
12:34Scalars and Vectors
Scalars and VectorsScalars and Vectors
Mr. Andersen explains the differences between scalar and vectors quantities. He also uses a demonstration to show the importance of vectors and vector addition. Intro Music Atribution Title: I4dsong_loop_main.wav Artist: CosmicD Link to sound: http://www.freesound.org/people/CosmicD/sounds/72556/ Creative Commons Atribution License -
 5:58
5:58Physics - Mechanics: Vectors (12 of 20) Product Of Vectors: Dot Product
Physics - Mechanics: Vectors (12 of 20) Product Of Vectors: Dot Product -
 23:31
23:31iTTV SPM Form 4 Physics Chapter 1 Scalar and Vector Quantities - Tuition/Lesson/Exam/Tips
iTTV SPM Form 4 Physics Chapter 1 Scalar and Vector Quantities - Tuition/Lesson/Exam/TipsiTTV SPM Form 4 Physics Chapter 1 Scalar and Vector Quantities - Tuition/Lesson/Exam/Tips
Chapter 01 : Introduction to Physics - Lesson 02: Scalar and Vector Quantities Hey Students. We are a private e-learning company which provide students with video classroom lessons for home study and revision. Our syllabus was developed for students who are in IGCSE, K-12, O-Level programs. Subscribe at www.ittv.com.my/fsl today for best study result. "Learn Well to Do Well" - iTTV Education. -
 4:38
4:38Basic Physics: Vector Measurements Vs. Scalar Measurements
Basic Physics: Vector Measurements Vs. Scalar MeasurementsBasic Physics: Vector Measurements Vs. Scalar Measurements
This is the the Basic Physics Series. In this lesson DrD, "The Explainer" explains the difference between vector and scalar measurements. This is an understandable explanation of another, often confusing topic. -
 12:04
12:04Physics Straight line motion Part 2 Scalar, vector, distance, displacement class 11 CBSE
Physics Straight line motion Part 2 Scalar, vector, distance, displacement class 11 CBSEPhysics Straight line motion Part 2 Scalar, vector, distance, displacement class 11 CBSE
Physics Straight line motion Part 2 Scalar, vector, distance, displacement class 11 CBSE -
 5:23
5:23AQA A level Physics Unit 2 Q1 Walk through. Scalars and vectors.
AQA A level Physics Unit 2 Q1 Walk through. Scalars and vectors.AQA A level Physics Unit 2 Q1 Walk through. Scalars and vectors.
AQA physics a level unit 2 mechanics. June 12 question 1 past paper walk through. Scalars vectors resolving vectors. -
 5:07
5:07Physics Motion part 3 (Scalar & vector quantity) CBSE class 9 IX
Physics Motion part 3 (Scalar & vector quantity) CBSE class 9 IX
- Charge (physics)
- Charge density
- Classical physics
- Coordinate system
- Current density
- Distance
- Electric charge
- Electric potential
- Energy density
- Euclidean vector
- Force
- Gravitation
- Improper rotation
- Invariant mass
- Lorentz scalar
- Magnetic charge
- Mass
- Matthew Sands
- Metric (mathematics)
- Number
- Orthonormal
- Physical quantity
- Physical unit
- Physics
- Pressure
- Proper length
- Proper rotation
- Proper time
- Pseudovector
- Quantity
- Relative scalar
- Richard Feynman
- Robert B. Leighton
- Scalar (mathematics)
- Scalar (physics)
- Scalar field
- Scalar field theory
- Spacetime
- Speed
- Stress-energy tensor
- Temperatures
- Theory of relativity
- Triple product
- Vector (geometric)
- Vector (physics)
- Velocity
-

New Scalar Model of Physics - Full Version
A New Model of Physics that address the anomalies of the Standard Model -

Introduction to Vectors and Scalars
Distance, displacement, speed and velocity. Difference between vectors and scalars More free lessons at: http://www.khanacademy.org/video?v=ihNZlp7iUHE -

Technical proof: scalar waves exist
-

The Scalar Product or Dot Product for Physics
An introduction to the scalar product of dot product for AP Physics. -

High School Physics: Vectors and Scalars
In this video Dan Fullerton provides a brief introduction to vectors and scalars for students in high school physics courses including Regents Physics, IB, AP Physics, and others. APlusPhysics.com provides a variety of free educational resources to assist students in finding success in high school physics courses such as Honors Physics, Regents Physics, and AP Physics. Resources include video mini-lessons, online tutorials, help forums, problem sets, downloads, and review books. You may also be interested in related videos in this series: https://www.youtube.com/playlist?list=PLB03A41EA88A8DE65 For more information, check out http://aplusphysics.com, and associated books in the series specific to courses: Regents Physics Essentials: http://aplusphysics.com/regents/ Honors Physics Essen... -

Physics Motion in plane part 1 (Introduction to Scalar and Vector) CBSE class 11
Physics Motion in plane part 1 (Introduction to Scalar and Vector) CBSE class 11 -

(7) IGCSE Physics in 60 Seconds - Vector and Scalar Quantities
A short and sweet video explaining about Vector and Scalar quantities! Created by a GCSE student, for GCSE students :) Like, Comment, Subscribe if you found this video helpful! Feel free to comment if you have any questions you would like to ask! Check out my blog :) - http://ohigetitnowebz.blogspot.co.uk/ Thanks for watching! - Music from www.freemusicforvideos.com -

Scalars and Vectors
Mr. Andersen explains the differences between scalar and vectors quantities. He also uses a demonstration to show the importance of vectors and vector addition. Intro Music Atribution Title: I4dsong_loop_main.wav Artist: CosmicD Link to sound: http://www.freesound.org/people/CosmicD/sounds/72556/ Creative Commons Atribution License -

-

iTTV SPM Form 4 Physics Chapter 1 Scalar and Vector Quantities - Tuition/Lesson/Exam/Tips
Chapter 01 : Introduction to Physics - Lesson 02: Scalar and Vector Quantities Hey Students. We are a private e-learning company which provide students with video classroom lessons for home study and revision. Our syllabus was developed for students who are in IGCSE, K-12, O-Level programs. Subscribe at www.ittv.com.my/fsl today for best study result. "Learn Well to Do Well" - iTTV Education. -

Basic Physics: Vector Measurements Vs. Scalar Measurements
This is the the Basic Physics Series. In this lesson DrD, "The Explainer" explains the difference between vector and scalar measurements. This is an understandable explanation of another, often confusing topic. -

Physics Straight line motion Part 2 Scalar, vector, distance, displacement class 11 CBSE
Physics Straight line motion Part 2 Scalar, vector, distance, displacement class 11 CBSE -

AQA A level Physics Unit 2 Q1 Walk through. Scalars and vectors.
AQA physics a level unit 2 mechanics. June 12 question 1 past paper walk through. Scalars vectors resolving vectors. -

-

-

IB Physics SL revision - Mechanics 1 - vectors vs scalars
In this first mechanics video, I show you the difference between vectors and scalars, and examples of each. For hundreds of free videos, one-to-one tutoring and revision courses, go to www.studynova.com -

Vectors in Physics, The Dot Product or The Scalar Product - College Physics Examples
Free Resources at JJtheTutor.com For the vectors A, B, and C in the figure, find the scalar products a dot b, b dot c, a dot c Dealing with products of vectors in college level physics problems. The dot product, the scalar product. -

Scalar Product and Vector Product Of two Vectors
Follow us at: https://plus.google.com/+tutorvista/ Check us out at http://www.tutorvista.com/content/physics/physics-iii/kinematics/cross-product.php Scalar Product The scalar product and the vector product are the two ways of multiplying vectors which see the most application in physics and astronomy. The scalar product of two vectors can be constructed by taking the component of one vector in the direction of the other and multiplying it times the magnitude of the other vector. Please like our facebook page http://www.facebook.com/tutorvista -

Urdu Physics Lecture About Vectors And Scalars
Visit http://urduphysicslectures.blogspot.com For More Urdu Physics Video Lectures Head To Tail Rule,Dot Product,Cross Product,Parallelogram Law Of Forces,Vector Addition and subtraction,Rectangular Components of Vector -

Physics Electricity part 3 (Current Scalar or vector) CBSE class 10 X
Physics Electricity part 3 (Current Scalar or vector) CBSE class 10 X -

Vectors & Scalars | AP Physics 1 & 2
Full lesson on vectors & scalars from Educator.com’s AP Physics 1 & 2 class. Want more video tutorials? Our full lesson includes in-depth explanations and even more worked out examples. ►See the entire syllabus at https://www.educator.com/physics/ap-physics-1-2/fullerton/?utm_source=YT&utm;_medium=SEO&utm;_campaign=APPHYS12YT In this video, we’ll discuss vectors & scalars. You'll learn about vector representations, graphical vector addition, graphical vector subtraction, vector components, and vector notation. We'll go over five full example problems on vector components, addition, and angle. Like other instructors such as Yau-Jong Twu, Flipping Physics, Bozeman Science, and Dan Fullerton? Our AP Physics instructor is pretty awesome too. Professor Fullerton obtained his B.S. and M.S. in... -

-

The dot product
Introduction to the vector dot product. More free lessons at: http://www.khanacademy.org/video?v=KDHuWxy53uM
New Scalar Model of Physics - Full Version
- Order: Reorder
- Duration: 92:31
- Updated: 28 Jun 2013
- views: 637
- published: 28 Jun 2013
- views: 637
Introduction to Vectors and Scalars
- Order: Reorder
- Duration: 8:39
- Updated: 11 Jun 2011
- views: 1816716
- published: 11 Jun 2011
- views: 1816716
Technical proof: scalar waves exist
- Order: Reorder
- Duration: 63:58
- Updated: 22 Aug 2013
- views: 21454
- published: 22 Aug 2013
- views: 21454
The Scalar Product or Dot Product for Physics
- Order: Reorder
- Duration: 10:00
- Updated: 20 Sep 2009
- views: 22022
- published: 20 Sep 2009
- views: 22022
High School Physics: Vectors and Scalars
- Order: Reorder
- Duration: 15:08
- Updated: 28 Jun 2011
- views: 55793
- published: 28 Jun 2011
- views: 55793
Physics Motion in plane part 1 (Introduction to Scalar and Vector) CBSE class 11
- Order: Reorder
- Duration: 11:00
- Updated: 12 Sep 2011
- views: 72415
- published: 12 Sep 2011
- views: 72415
(7) IGCSE Physics in 60 Seconds - Vector and Scalar Quantities
- Order: Reorder
- Duration: 1:25
- Updated: 10 Aug 2013
- views: 4424
- published: 10 Aug 2013
- views: 4424
Scalars and Vectors
- Order: Reorder
- Duration: 12:34
- Updated: 23 Jan 2011
- views: 129134
- published: 23 Jan 2011
- views: 129134
Physics - Mechanics: Vectors (12 of 20) Product Of Vectors: Dot Product
- Order: Reorder
- Duration: 5:58
- Updated: 07 Aug 2013
- views: 18288
iTTV SPM Form 4 Physics Chapter 1 Scalar and Vector Quantities - Tuition/Lesson/Exam/Tips
- Order: Reorder
- Duration: 23:31
- Updated: 15 Sep 2015
- views: 828
- published: 15 Sep 2015
- views: 828
Basic Physics: Vector Measurements Vs. Scalar Measurements
- Order: Reorder
- Duration: 4:38
- Updated: 09 Mar 2014
- views: 1955
- published: 09 Mar 2014
- views: 1955
Physics Straight line motion Part 2 Scalar, vector, distance, displacement class 11 CBSE
- Order: Reorder
- Duration: 12:04
- Updated: 07 Aug 2011
- views: 40352
- published: 07 Aug 2011
- views: 40352
AQA A level Physics Unit 2 Q1 Walk through. Scalars and vectors.
- Order: Reorder
- Duration: 5:23
- Updated: 30 Oct 2014
- views: 3002
- published: 30 Oct 2014
- views: 3002
Physics Motion part 3 (Scalar & vector quantity) CBSE class 9 IX
- Order: Reorder
- Duration: 5:07
- Updated: 15 Jun 2013
- views: 16853
Physics Work Energy Power part 2 (Scalar Products) CBSE class 11
- Order: Reorder
- Duration: 10:46
- Updated: 26 Aug 2011
- views: 28581
IB Physics SL revision - Mechanics 1 - vectors vs scalars
- Order: Reorder
- Duration: 9:08
- Updated: 16 Mar 2015
- views: 5159
- published: 16 Mar 2015
- views: 5159
Vectors in Physics, The Dot Product or The Scalar Product - College Physics Examples
- Order: Reorder
- Duration: 4:56
- Updated: 27 May 2013
- views: 1217
- published: 27 May 2013
- views: 1217
Scalar Product and Vector Product Of two Vectors
- Order: Reorder
- Duration: 3:43
- Updated: 26 Apr 2010
- views: 38214
- published: 26 Apr 2010
- views: 38214
Urdu Physics Lecture About Vectors And Scalars
- Order: Reorder
- Duration: 25:27
- Updated: 18 Feb 2011
- views: 35712
- published: 18 Feb 2011
- views: 35712
Physics Electricity part 3 (Current Scalar or vector) CBSE class 10 X
- Order: Reorder
- Duration: 1:58
- Updated: 16 Apr 2013
- views: 28018
- published: 16 Apr 2013
- views: 28018
Vectors & Scalars | AP Physics 1 & 2
- Order: Reorder
- Duration: 25:06
- Updated: 27 Mar 2013
- views: 3635
- published: 27 Mar 2013
- views: 3635
Physics Motion in plane part 2 (Combination of Scalar) CBSE class 11
- Order: Reorder
- Duration: 4:28
- Updated: 12 Sep 2011
- views: 31839
The dot product
- Order: Reorder
- Duration: 10:33
- Updated: 09 Aug 2008
- views: 252374
- published: 09 Aug 2008
- views: 252374
-

Physics - Advanced E&M;: Ch 1 Math Concepts (13 of 55) What is the Laplacian of a Scalar (Field)?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain, develop the equation, and give examples of the Laplacian of a scalar (field). Next video in this series can be seen at: https://youtu.be/2VXFzhcGT3U -

-

-

Vector and scalar quantities
GCSE Physics -

Scalar and Vector Quantities
Useful for CBSE, ICSE, NCERT & International Students Grade 7 Subject: Physics Lesson : Motion and Time Topic: Scalar and Vector Quantities • Scalar is the measurement of a medium strictly in magnitude. • Vector is a measurement that refers to both the magnitude of the medium as well as the direction of the movement the medium has taken. Visit www.oztern.com to find personalized test preparation solutions for Pre Medical - AIPMT, AIIMS, JIPMER, State, Pre Engineering - IIT JEE, JEE MAIN, BITSAT, State and Foundations - Class 6 to 10. -

Scalar and Vector Quantities
Scalars Vectors Vector Addition Resolution Of Vectors Like Our Facebook Page: https://www.facebook.com/physicspassion/ -

Scalar and Vector Quantities
Useful for CBSE, ICSE, NCERT & International Students Grade : 9 Subject :Physics Lesson : Motion Topic: Scalar and Vector Quantities Acceleration is a vector quantity that is defined as the rate at which an object changes its velocity. An object is accelerating if it is changing its velocity. Visit www.oztern.com to find personalized test preparation solutions for Pre Medical - AIPMT, AIIMS, JIPMER, State, Pre Engineering - IIT JEE, JEE MAIN, BITSAT, State and Foundations - Class 6 to 10. -

-

-

-

-

Mathematical Physics Class 7 - Scalar Triple Product
Here, we have discussed more about the Scalar Triple products and its physical interpretation. -

Mathematical Physics Class 5 - More on Scalar Product
Here we have discussed more on vector scalar products. We also discuss the unit vector scalar product and the law of cosine -

Scalar Mathematics for Scalar Motion & Scalar Motion for Scalar Physics - Part IV
On this episode of Honest Investigators Talk Shop, we present how understanding the true nature of numbers and the reciprocal nature of space and time leads to amazing results in understanding the observed physical universe. Both the mathematics and the physics of the Reciprocal System of Theory present mind-boggling possibilities for the future of science. Please join us for this episode of "Honest Investigators Talk Shop, live! -

Scalar (physics)
Scalar (physics) In physics, a scalar is a one-dimensional physical quantity, i.e.one that can be described by a single real number (sometimes signed, often with units), in other words a scalar is a physical quantity that only has magnitude but no direction, unlike (or as a special case of) vectors, tensors, etc. -Video is targeted to blind users Attribution: Article text available under CC-BY-SA image source in video https://www.youtube.com/watch?v=8kHzKcWSqQ0 -

Scalar field theory
Scalar field theory In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields.A scalar field is invariant under any Lorentz transformation. -Video is targeted to blind users Attribution: Article text available under CC-BY-SA image source in video https://www.youtube.com/watch?v=74qtcbQ4hEA -

Scalar Mathematics for Scalar Motion & Scalar Motion for Scalar Physics - Part III
In this episode we continue with part III of Lecture 3, taking the idea of multi-dimensional scalar algebra to the next level that should enable us to calculate the properties of the combinations of scalar motion, which correspond to those of the first family of the observed standard model of particle physics. See video synced with slides on our website: http://www.lrcphysics.com/lrc-lectures/?SSScrollPosition=0 -

Scalar field
Scalar field In mathematics and physics, a scalar field associates a scalar value to every point in a space.The scalar may either be a mathematical number or a physical quantity. =======Image-Copyright-Info======= Image is in public domain Author-Info: Lucas V. Barbosa Image Source: https://en.wikipedia.org/wiki/File:Scalar_field.png =======Image-Copyright-Info======== -Video is targeted to blind users Attribution: Article text available under CC-BY-SA image source in video https://www.youtube.com/watch?v=XEPo4wHhM1Y -

Scalar Waves: The Future-Now Medicine is Photonic Light
Light, the Medicine of the Future. Matrices of blue-white starlight, beaming from all the stars in the universe, converging at the body of the meditator, at her open receptive heart. Our pineal glands, mini-photon generators, the original little particle accelerators. The physics of higher multi-dimensional perception understands photons/light particles to be highly intelligent and conscious: we can communicate with the stars. Photon friends are awesome, helpful, and fract-all! I used to have dreams and memories early on in my awakening/remembering process in which I lived on a planet where everyone bathed regularly in starlight for nourishment and rejuvination as well as channeled the stars' energies into art, music, lovemaking etc. Note: scalar waves also neutralize less harmonious EM... -

Scalar Mathematics for Scalar Motion & Scalar Motion for Scalar Physics
Well, after nine years, the LRC's lecture on the Reciprocal System of Mathematics (RSM) is about to begin. In this part I of the lecture, Lecture 3 of our lecture series, we unveil an amazing correspondence between a new interpretation of the binomial expansion, as seen in the Greek Tetraktys, and the scalar expansion of rational numbers, in three dimensions. After we see this remarkable unification of scalar numbers, we are delighted to discover their physical connections. It's fascinating. Please join us for this episode of "Honest Investigators Talk Shop." -

Physics Introduction | Ch4 | Work, Power & Energy | Scalar Dot Product?
جامعة الملك خالد - عمادة التعلم الإلكتروني المقررات المفتوحة - مقدمة فيزياء Physics Introduction - 102 phys Chapter 4 : Work, Power & Energy 1. Scalar Dot Product? 2. Work 3. Kinetic Energy 4. Example -

Differential of a Scalar Function - Chain Rule - Special General Relativity - Mathematical Physics
Using component notation to show how a differential of a scalar field is derived. Using index gymnastics and Einstein summation convention. There is an implied summation at the end, alpha is an upper and lower index. -

Physics 3U - Kinematics - Scalar vs. Vector Quantity
Quick video describing the difference between a vector and scalar quantity. Subscribe for more!
Physics - Advanced E&M;: Ch 1 Math Concepts (13 of 55) What is the Laplacian of a Scalar (Field)?
- Order: Reorder
- Duration: 8:18
- Updated: 13 Mar 2016
- views: 183
Fsc Book 1 Physics Chapter 2 - LEC 5 - Scalar Product
- Order: Reorder
- Duration: 26:53
- Updated: 12 Mar 2016
- views: 13
Physics - Advance E&M;: Ch 1 Math Concepts (5 of 55) What is the Scalar Product?
- Order: Reorder
- Duration: 6:18
- Updated: 05 Mar 2016
- views: 30
Vector and scalar quantities
- Order: Reorder
- Duration: 4:30
- Updated: 01 Mar 2016
- views: 1
Scalar and Vector Quantities
- Order: Reorder
- Duration: 0:45
- Updated: 30 Dec 2015
- views: 4
- published: 30 Dec 2015
- views: 4
Scalar and Vector Quantities
- Order: Reorder
- Duration: 10:31
- Updated: 15 Dec 2015
- views: 7
- published: 15 Dec 2015
- views: 7
Scalar and Vector Quantities
- Order: Reorder
- Duration: 1:19
- Updated: 26 Nov 2015
- views: 14
- published: 26 Nov 2015
- views: 14
Scalar Mathematics for Scalar Motion and Scalar Motion for Scalar Physics, Part VII
- Order: Reorder
- Duration: 72:51
- Updated: 28 Feb 2016
- views: 3
Scalar Mathematics for Scalar Motion and Scalar Motion for Scalar Physics -Part VI
- Order: Reorder
- Duration: 50:59
- Updated: 21 Feb 2016
- views: 13
Scalar quantities
- Order: Reorder
- Duration: 1:01
- Updated: 18 Feb 2016
- views: 0
Scalar Mathematics for Scalar Motion and Scalar Motion for Scalar Physics Part V
- Order: Reorder
- Duration: 61:04
- Updated: 11 Feb 2016
- views: 12
Mathematical Physics Class 7 - Scalar Triple Product
- Order: Reorder
- Duration: 42:35
- Updated: 10 Feb 2016
- views: 2381
- published: 10 Feb 2016
- views: 2381
Mathematical Physics Class 5 - More on Scalar Product
- Order: Reorder
- Duration: 39:06
- Updated: 08 Feb 2016
- views: 0
- published: 08 Feb 2016
- views: 0
Scalar Mathematics for Scalar Motion & Scalar Motion for Scalar Physics - Part IV
- Order: Reorder
- Duration: 71:36
- Updated: 31 Jan 2016
- views: 17
- published: 31 Jan 2016
- views: 17
Scalar (physics)
- Order: Reorder
- Duration: 4:25
- Updated: 29 Jan 2016
- views: 0
- published: 29 Jan 2016
- views: 0
Scalar field theory
- Order: Reorder
- Duration: 18:12
- Updated: 29 Jan 2016
- views: 2
- published: 29 Jan 2016
- views: 2
Scalar Mathematics for Scalar Motion & Scalar Motion for Scalar Physics - Part III
- Order: Reorder
- Duration: 54:11
- Updated: 24 Jan 2016
- views: 18
- published: 24 Jan 2016
- views: 18
Scalar field
- Order: Reorder
- Duration: 5:34
- Updated: 22 Jan 2016
- views: 0
- published: 22 Jan 2016
- views: 0
Scalar Waves: The Future-Now Medicine is Photonic Light
- Order: Reorder
- Duration: 11:50
- Updated: 12 Jan 2016
- views: 131
- published: 12 Jan 2016
- views: 131
Scalar Mathematics for Scalar Motion & Scalar Motion for Scalar Physics
- Order: Reorder
- Duration: 89:51
- Updated: 10 Jan 2016
- views: 20
- published: 10 Jan 2016
- views: 20
Physics Introduction | Ch4 | Work, Power & Energy | Scalar Dot Product?
- Order: Reorder
- Duration: 13:46
- Updated: 02 Dec 2015
- views: 118
- published: 02 Dec 2015
- views: 118
Differential of a Scalar Function - Chain Rule - Special General Relativity - Mathematical Physics
- Order: Reorder
- Duration: 3:30
- Updated: 13 Oct 2015
- views: 104
- published: 13 Oct 2015
- views: 104
Physics 3U - Kinematics - Scalar vs. Vector Quantity
- Order: Reorder
- Duration: 1:52
- Updated: 24 Sep 2015
- views: 22
- published: 24 Sep 2015
- views: 22
-

-

Physics 240 Lecture 6 - Scalar Product and Cartesian Coordinate System
Professor Jerzy Wrobel explains introduces scalar product and shows how to identify components of vectors. -

Physics 240 - Lecture 3 - Scalar Quantities
Professor Jerzy Wrobel discussed properties of scalar quantities and introduces concepts of time, distance, mass and length. -

PHYSICS - MATHEMATICS FOR PHYSICS - Introduction to Scalar & Vector - Expert Speak - Crack IIT JEE
IIT JEE - PHYSICS - MATHEMATICS FOR PHYSICS - Introduction to Scalar & Vector. Scalar - Physical quantities which have magnitude only. Eg: Speed, Distance, Mass etc. Vector - Physical quantities which have magnitude as well as direction. Eg: Displacement, Velocity, Acceleration, Force, Momentum etc. This video takes you deeper into the section of vectors and scalars and also some problems and their solutions. It is a part of our IIT JEE video lecture series by Rajiv Sir - Ex Head Faculty at premier institutes for IIT JEE preparation - Resonance and Narayana. Rajiv qualified with a B.E. from IIT Bombay and has over 10 years of IIT JEE coaching experience. For more such helpful videos on IIT JEE Exam subscribe to our Channel. To know more kindly go on this link- https://goo.gl/Kzjptk Y... -

Scalar Mathematics for Scalar Motion & Scalar Motion for Scalar Physics - Part IIa
This program features a remake of Part II of Lecture 3. Part I was presented on the previous program. This lecture has to do with the unification of discrete numbers and continuous magnitudes, not by squaring the circle, but by showing how 3D discrete numbers contain 3D continuous magnitudes, as shown by the correspondence between the binomial expansion of the Greek Tetraktys and the 3D scalar expansion of Larson's Cube. Please join us to discuss it on this episode of the Honest Investigators Talk Shop show -

Tom Bearden (The Physics of Psionics) Radionics Action At A Distance
The actual PHYSICS of how your abilities work. VERY useful, (and also research his references). Previously suppressed information on scalar physics. (Radionics machines are machines that boost your psychic and psionic abilities) -

Mod-01 Lec-01 Scalar field and its Gradient
Electromagnetic Theory by Prof. D.K. Ghosh,Department of Physics,IIT Bombay.For more details on NPTEL visit http://nptel.ac.in -

Scalar Waves used in Mind Control
20 November 2014 targeted individuals (ti), victims of mind control, organized their first conference in the world to alarm about mind control and covert harassment. That technology is at least 60 years old and hidden behind secret physics. That makes it difficult to detect and protect against mind control. The secret physics are scalar waves, an unknown type of waves detected by Nikola Tesla for more than 100 years ago. Scalar waves have totally different qualities compared to electromagnetic waves. Scalar waves are kept secret because they describe how to use free energy (neutrinos) and because they are used to control humans mind, brain and body. The aims of the Covert Harassment Conference 2014: - To challenge general ignorance, governments denial and mainstream media silence regarding... -

Physics(Lec9,Scalar product(Kinematics),Class 11,CBSE,XI
11 Class Physics,Scalar product(Kinematics),CBSE,English-Hindi Mix.Explains in detail one of the two ways of multiplication of two vectors; the scalar product also known as dot product, highlighting the concept behind it and its applications in life. Buy Full Video For Rs. 200 At www.sci4you.com Buy Full Video For Rs. 200 At www.sci4you.com Buy Full Video For Rs. 200 At www.sci4you.com -

Scalar Triple Product and Vectors Practice Problems - IIT JEE Main & Advanced Physics Video Lecture
IIT JEE Main and Advanced Physics Video Lectures and Study Material developed by highly experienced and dedicated faculty team of Rao IIT Academy. Visit http://www.raoiit.com or email studentcare@raoiit.com for any query or doubt related to your IIT JEE Preparation. Want to be the Topper ??? Learn Scalar Triple Product and Vectors Practice Problems from Rao IIT Academy. Prepare for your Boards and New IIT-JEE Pattern - JEE Main and JEE Advanced / MH-CET / BITSAT / VIT / SRM / Manipal and other Competitive Exams with Rao IIT Academy. ...................................... Subscribe to Rao IIT Academy YouTube channel - http://www.youtube.com/RaoIITAcademy Like us on Facebook - https://www.facebook.com/Raoiit Follow us on Twitter - https://twitter.com/rao_iit +1 on Google Plus - https://plu...
XI-4.1Vector Introduction (2014) Pradeep Kshetrapal Physics
- Order: Reorder
- Duration: 62:06
- Updated: 20 Jul 2014
- views: 28731
Physics 240 Lecture 6 - Scalar Product and Cartesian Coordinate System
- Order: Reorder
- Duration: 43:15
- Updated: 10 Feb 2014
- views: 1624
- published: 10 Feb 2014
- views: 1624
Physics 240 - Lecture 3 - Scalar Quantities
- Order: Reorder
- Duration: 49:09
- Updated: 19 Jan 2010
- views: 3946
- published: 19 Jan 2010
- views: 3946
PHYSICS - MATHEMATICS FOR PHYSICS - Introduction to Scalar & Vector - Expert Speak - Crack IIT JEE
- Order: Reorder
- Duration: 44:38
- Updated: 20 Nov 2014
- views: 163
- published: 20 Nov 2014
- views: 163
Scalar Mathematics for Scalar Motion & Scalar Motion for Scalar Physics - Part IIa
- Order: Reorder
- Duration: 66:20
- Updated: 21 Jan 2016
- views: 13
- published: 21 Jan 2016
- views: 13
Tom Bearden (The Physics of Psionics) Radionics Action At A Distance
- Order: Reorder
- Duration: 95:40
- Updated: 11 Aug 2014
- views: 15688
- published: 11 Aug 2014
- views: 15688
Mod-01 Lec-01 Scalar field and its Gradient
- Order: Reorder
- Duration: 48:26
- Updated: 12 Mar 2015
- views: 16034
- published: 12 Mar 2015
- views: 16034
Scalar Waves used in Mind Control
- Order: Reorder
- Duration: 62:33
- Updated: 22 Nov 2014
- views: 11559
- published: 22 Nov 2014
- views: 11559
Physics(Lec9,Scalar product(Kinematics),Class 11,CBSE,XI
- Order: Reorder
- Duration: 26:40
- Updated: 21 Jun 2015
- views: 96
- published: 21 Jun 2015
- views: 96
Scalar Triple Product and Vectors Practice Problems - IIT JEE Main & Advanced Physics Video Lecture
- Order: Reorder
- Duration: 28:32
- Updated: 08 May 2014
- views: 5010
- published: 08 May 2014
- views: 5010
- Playlist
- Chat
- Playlist
- Chat

New Scalar Model of Physics - Full Version
- Report rights infringement
- published: 28 Jun 2013
- views: 637

Introduction to Vectors and Scalars
- Report rights infringement
- published: 11 Jun 2011
- views: 1816716

Technical proof: scalar waves exist
- Report rights infringement
- published: 22 Aug 2013
- views: 21454

The Scalar Product or Dot Product for Physics
- Report rights infringement
- published: 20 Sep 2009
- views: 22022

High School Physics: Vectors and Scalars
- Report rights infringement
- published: 28 Jun 2011
- views: 55793

Physics Motion in plane part 1 (Introduction to Scalar and Vector) CBSE class 11
- Report rights infringement
- published: 12 Sep 2011
- views: 72415

(7) IGCSE Physics in 60 Seconds - Vector and Scalar Quantities
- Report rights infringement
- published: 10 Aug 2013
- views: 4424

Scalars and Vectors
- Report rights infringement
- published: 23 Jan 2011
- views: 129134

Physics - Mechanics: Vectors (12 of 20) Product Of Vectors: Dot Product
- Report rights infringement
- published: 07 Aug 2013
- views: 18288

iTTV SPM Form 4 Physics Chapter 1 Scalar and Vector Quantities - Tuition/Lesson/Exam/Tips
- Report rights infringement
- published: 15 Sep 2015
- views: 828

Basic Physics: Vector Measurements Vs. Scalar Measurements
- Report rights infringement
- published: 09 Mar 2014
- views: 1955

Physics Straight line motion Part 2 Scalar, vector, distance, displacement class 11 CBSE
- Report rights infringement
- published: 07 Aug 2011
- views: 40352

AQA A level Physics Unit 2 Q1 Walk through. Scalars and vectors.
- Report rights infringement
- published: 30 Oct 2014
- views: 3002

Physics Motion part 3 (Scalar & vector quantity) CBSE class 9 IX
- Report rights infringement
- published: 15 Jun 2013
- views: 16853
- Playlist
- Chat

Physics - Advanced E&M;: Ch 1 Math Concepts (13 of 55) What is the Laplacian of a Scalar (Field)?
- Report rights infringement
- published: 13 Mar 2016
- views: 183


Physics - Advance E&M;: Ch 1 Math Concepts (5 of 55) What is the Scalar Product?
- Report rights infringement
- published: 05 Mar 2016
- views: 30

Vector and scalar quantities
- Report rights infringement
- published: 01 Mar 2016
- views: 1

Scalar and Vector Quantities
- Report rights infringement
- published: 30 Dec 2015
- views: 4

Scalar and Vector Quantities
- Report rights infringement
- published: 15 Dec 2015
- views: 7

Scalar and Vector Quantities
- Report rights infringement
- published: 26 Nov 2015
- views: 14

Scalar Mathematics for Scalar Motion and Scalar Motion for Scalar Physics, Part VII
- Report rights infringement
- published: 28 Feb 2016
- views: 3

Scalar Mathematics for Scalar Motion and Scalar Motion for Scalar Physics -Part VI
- Report rights infringement
- published: 21 Feb 2016
- views: 13

Scalar quantities
- Report rights infringement
- published: 18 Feb 2016
- views: 0

Scalar Mathematics for Scalar Motion and Scalar Motion for Scalar Physics Part V
- Report rights infringement
- published: 11 Feb 2016
- views: 12

Mathematical Physics Class 7 - Scalar Triple Product
- Report rights infringement
- published: 10 Feb 2016
- views: 2381

Mathematical Physics Class 5 - More on Scalar Product
- Report rights infringement
- published: 08 Feb 2016
- views: 0

Scalar Mathematics for Scalar Motion & Scalar Motion for Scalar Physics - Part IV
- Report rights infringement
- published: 31 Jan 2016
- views: 17
- Playlist
- Chat

XI-4.1Vector Introduction (2014) Pradeep Kshetrapal Physics
- Report rights infringement
- published: 20 Jul 2014
- views: 28731

Physics 240 Lecture 6 - Scalar Product and Cartesian Coordinate System
- Report rights infringement
- published: 10 Feb 2014
- views: 1624

Physics 240 - Lecture 3 - Scalar Quantities
- Report rights infringement
- published: 19 Jan 2010
- views: 3946

PHYSICS - MATHEMATICS FOR PHYSICS - Introduction to Scalar & Vector - Expert Speak - Crack IIT JEE
- Report rights infringement
- published: 20 Nov 2014
- views: 163

Scalar Mathematics for Scalar Motion & Scalar Motion for Scalar Physics - Part IIa
- Report rights infringement
- published: 21 Jan 2016
- views: 13

Tom Bearden (The Physics of Psionics) Radionics Action At A Distance
- Report rights infringement
- published: 11 Aug 2014
- views: 15688

Mod-01 Lec-01 Scalar field and its Gradient
- Report rights infringement
- published: 12 Mar 2015
- views: 16034

Scalar Waves used in Mind Control
- Report rights infringement
- published: 22 Nov 2014
- views: 11559

Physics(Lec9,Scalar product(Kinematics),Class 11,CBSE,XI
- Report rights infringement
- published: 21 Jun 2015
- views: 96

Scalar Triple Product and Vectors Practice Problems - IIT JEE Main & Advanced Physics Video Lecture
- Report rights infringement
- published: 08 May 2014
- views: 5010
Cynthia Lee Fontaine on her "Drag Race" elimination and battle with cancer
Edit The Examiner 22 Mar 2016Islamic State issues statement promising ‘dark days’ ahead
Edit Indian Express 23 Mar 2016Australian Police Arrest 16-Year-Old Student Suspected Of Raising Funds For Islamic State
Edit WorldNews.com 23 Mar 2016FBI's New Unlocking Method May Resolve Terrorist's iPhone 5C, But Scares Apple
Edit WorldNews.com 23 Mar 2016Raising the Social Security Retirement Age Would Pose Hardship on Millions of American Workers (CEPR - Center for Economic and Policy Research)
Edit Public Technologies 23 Mar 2016School Specialty’s Sportime® Celebrates 50 Years of Innovation in Physical Education (School Specialty Inc)
Edit Public Technologies 23 Mar 2016Exercise recommendations to counter health-detrimental passivity in old people (Umeå universitet)
Edit Public Technologies 23 Mar 2016Jump-start your program's physical activities with a PEP grant IN: FUNDING (3/22/16) (Afterschool Alliance)
Edit Public Technologies 23 Mar 2016Physical activity encouraged more for boys than girls: UC research (University of Canberra)
Edit Public Technologies 23 Mar 2016Exercise Slows Brain Aging By 10 Years
Edit Time Magazine 23 Mar 2016UCSB Professor Joe Incandela Named 61st Faculty Research Lecturer (University of California - Santa Barbara)
Edit Public Technologies 23 Mar 2016VIAREGGIO CUP 2016, COACH BROCCHI: "THIS GAME WILL BE USED AS A LESSON” (Milan Associazione Calcio SpA)
Edit Public Technologies 23 Mar 2016Acupuncture licensing requirements pass Senate (KHI - Kansas Health Institute)
Edit Public Technologies 23 Mar 2016Paracetamol ‘not clinically effective’ in treating joint pain
Edit Indian Express 23 Mar 2016$5.55 Billion Data Center Physical Security Market Report - Forecasts from 2016 to 2021 - ...
Edit Business Wire 23 Mar 2016'Digi transformation is GE's core growth'
Edit Deccan Herald 23 Mar 2016Emmy Noether revolutionized mathematics — and still faced sexism all her life
Edit Vox 23 Mar 2016- 1
- 2
- 3
- 4
- 5
- Next page »







