- published: 24 Apr 2016
- views: 3465
- published: 25 Apr 2016
- views: 14208
- published: 25 Apr 2016
- views: 6405
- published: 22 Apr 2016
- views: 103030
- published: 23 Apr 2016
- views: 202
- published: 20 Apr 2016
- views: 21450
- published: 25 Apr 2016
- views: 1153
- published: 24 Apr 2016
- views: 960
- published: 25 Apr 2016
- views: 31
- published: 23 Mar 2016
- views: 464

In geometry, the centre (or center) (from Greek κέντρο) of an object is a point in some sense in the middle of the object. If geometry is regarded as the study of isometry groups then the centre is a fixed point of the isometries.
The centre of a circle is the point equidistant from the points on the edge. Similarly the centre of a sphere is the point equidistant from the points on the surface, and the centre of a line segment is the midpoint of the two ends.
For objects with several symmetries, the centre of symmetry is the point left unchanged by the symmetric actions. So the centre of a square, rectangle, rhombus or parallelogram is where the diagonals intersect, this being (amongst other properties) the fixed point of rotational symmetries. Similarly the centre of an ellipse is where the axes intersect.
Main article : Triangle centre
Several special points of a triangle are often described as triangle centres: the circumcentre, centroid or centre of mass, incentre, excentres, orthocentre, nine-point centre. For an equilateral triangle, these (except for the excentres) are the same point, which lies at the intersection of the three axes of symmetry of the triangle, one third of the distance from its base to its apex.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
Center or centre may refer to:
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.

Geometry (Ancient Greek: γεωμετρία; geo- "earth", -metria "measurement") is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer. Geometry arose independently in a number of early cultures as a body of practical knowledge concerning lengths, areas, and volumes, with elements of a formal mathematical science emerging in the West as early as Thales (6th Century BC). By the 3rd century BC geometry was put into an axiomatic form by Euclid, whose treatment—Euclidean geometry—set a standard for many centuries to follow.Archimedes developed ingenious techniques for calculating areas and volumes, in many ways anticipating modern integral calculus. The field of astronomy, especially mapping the positions of the stars and planets on the celestial sphere and describing the relationship between movements of celestial bodies, served as an important source of geometric problems during the next one and a half millennia. Both geometry and astronomy were considered in the classical world to be part of the Quadrivium, a subset of the seven liberal arts considered essential for a free citizen to master.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...

-
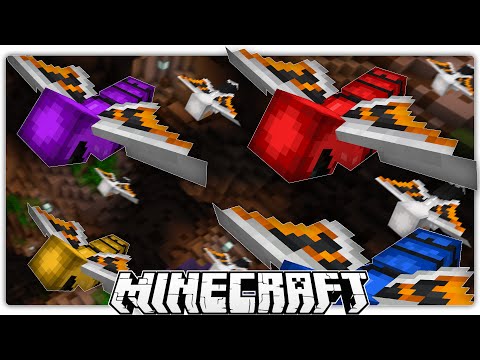 15:22
15:22JOURNEY TO THE CENTER OF PLANET MINECRAFT!! | Terra Swoop Force Custom Map Adventure
JOURNEY TO THE CENTER OF PLANET MINECRAFT!! | Terra Swoop Force Custom Map AdventureJOURNEY TO THE CENTER OF PLANET MINECRAFT!! | Terra Swoop Force Custom Map Adventure
JOURNEY TO THE CENTER OF PLANET MINECRAFT!! | Terra Swoop Force Custom Map Adventure Leave a like for Part 2 :D | Don't miss a vid! ►http://bit.ly/SubLog Support The Mapmakers! https://www.patreon.com/Noxcrew Terra Swoop Force is a team of scientists who have taken it upon themselves to harvest valuable minerals from the center of the Earth. A mission gone astray has left behind two scientists, and your job is to travel to the core of the planet and retrieve them. Are you up to the task!? _ ► Facebook http://facebook.com/Logdotzip ► Twitch http://twitch.tv/Logdotzip ► Twitter http://twitter.com/Logdotzip ► Instagram http://instagram.com/Logdotzip _ Minecraft Terra Swoop Force Map Download http://noxcrew.com/threads/terra-swoop-force-an-arcadey-minecraft-adventure-map-mc1-9-2.2773/ by Noxite: https://twitter.com/AlmightyNoxite by Avondale: https://twitter.com/avondale1718 and the NoxCrew! http://twitter.com/Noxcrew Music by Shag http://facebook.com/shagbeats All music used with permission from its creator. -
 7:52
7:52Things guitar center employees say
Things guitar center employees say -
 25:09
25:09JOURNEY TO THE CENTER OF THE EARTH IN MINECRAFT!
JOURNEY TO THE CENTER OF THE EARTH IN MINECRAFT!JOURNEY TO THE CENTER OF THE EARTH IN MINECRAFT!
An amazing Minecraft Map with a Journey to the center of the Earth! My Gaming Channel: http://www.youtube.com/VikkstarPlays Follow me on TWITTER: http://twitter.com/#!/Vikkstar123 Like my Facebook Page: http://www.facebook.com/Vikkstar123 My Instagram: http://instagram.com/Vikkstagram The Pack: https://www.youtube.com/Lachlan https://www.youtube.com/PrestonPlayz https://www.youtube.com/MrWoofless https://www.youtube.com/JeromeASF https://www.youtube.com/TheBajanCanadian My Servers: http://treasurewars.net/ IP: treasurewars.net My capture card: http://e.lga.to/v Follow me on Twitch for Livestreams: http://www.twitch.tv/vikkstar123 Check out my other channels linked below: FPS & More: http://www.youtube.com/Vikkstar123 Lets Play: http://www.youtube.com/VikkstarPlays Map: http://noxcrew.com/threads/terra-swoop-force-an-arcadey-minecraft-adventure-map-mc1-9-2.2773/ By The Noxcrew: http://noxcrew.com/ -
 14:33
14:33Heftiges Acer Event im World Trade Center!
Heftiges Acer Event im World Trade Center!Heftiges Acer Event im World Trade Center!
Heute ging auf zum Acer Event, dass doch tatsächlich oben in einem der New-Yorker World-Trade-Center Türme stattgefunden hat! Was da so alles spannendes Vorgestellt wurde und noch viel mehr, seht ihr in diesem Vlog. Viel Spaß! Mein Reise-Vlog Setup: Kamera: http://amzn.to/1Xgp1qX Objektiv: http://amzn.to/1YkCTxc Mikrofon: http://amzn.to/1IFqmRq Stativ: http://amzn.to/1Xgp8Tb Actioncam: http://amzn.to/1jsccaB Rucksack: http://amzn.to/1N9yeqL Kann Spuren der Musik von www.epidemicsound.com, Music4Montage und The Passion Hifi enthalten ;) -------------------------------------------------------------- Twitter: http://www.twitter.com/felixba Facebook: http://www.facebook.com/felixbaTV Instagram: http://www.instagram.com/felixba Hauptkanal auf Youtube: http://www.youtube.com/felixba94 Meine Videoausrüstung: http://astore.amazon.de/wwwyoutube066-21 -------------------------------------------------------------- Manche Links in der Videobeschreibung können Afilliate-Links sein. Wenn ihr über die Links etwas kauft, bekomme ich eine kleine Provision, ohne dass sich der Preis für euch ändert. Danke für den netten Support! -
 1:45
1:4516 Secrets Call Center Employees Won’t Tell You
16 Secrets Call Center Employees Won’t Tell You16 Secrets Call Center Employees Won’t Tell You
“The more upset you get, the funnier it is to me!” Check out more awesome videos at BuzzFeedVideo! http://bit.ly/YTbuzzfeedvideo MUSIC The Morning Show Licensed via Warner Chappell Production Music Inc. SFX provided by Audioblocks. (https://www.Audioblocks.com) Made by BFMP www.buzzfeed.com/videoteam + Rosa Pasquarella www.twitter.com/whatrosasaid Toni Del Sorbo https://www.facebook.com/tonidelsorbo/ Deyo Forteza Instagram: @le_deyo STILLS Business telephone with extensions on desk in office Hemera Technologies / Thinkstockphotos.com Film Footage courtesy of Shutterstock, Inc. Used with Permission BASED ON THIS BUZZFEED POST: http://www.buzzfeed.com/michaelblackmon/23-secrets-call-center-employees-wont-tell-you GET MORE BUZZFEED: www.buzzfeed.com/videoteam www.facebook.com/buzzfeedvideo www.instagram.com/buzzfeedvideo www.buzzfeed.com/video www.youtube.com/buzzfeedvideo www.youtube.com/buzzfeedyellow www.youtube.com/buzzfeedblue www.youtube.com/buzzfeedviolet BUZZFEED VIDEO BuzzFeed Motion Picture’s flagship channel. Sometimes funny, sometimes serious, always shareable. New videos posted daily! Subscribe to BuzzFeedVideo today! http://bit.ly/YTbuzzfeedvideo -
 0:42
0:42Donald Trump uses terrible Indian accent ,Trump: impersonates Indian call-center worker
Donald Trump uses terrible Indian accent ,Trump: impersonates Indian call-center workerDonald Trump uses terrible Indian accent ,Trump: impersonates Indian call-center worker
Donald Trump uses terrible Indian accent ,Trump: impersonates Indian call-center worker trump indian accent,Donald trump indian accent,Indian Accent,fake Indian Accent,Trump uses fake Indian accent,impersonates Indian call-center worker,Indian call-center,Indian call-center worker,Donald Trump - American Politician,trump indiana,donald trump rally,gop polls,how old is donald trump,trump delegate,trump delegate count,trump,trump news,hillary clinton,bernie sanders,debate,president,trump,donald trump,trump india,india,trump call center -
 6:16
6:16Things guitar center employees say (BLOOPERS)
Things guitar center employees say (BLOOPERS)Things guitar center employees say (BLOOPERS)
Watch some of my other videos: The DickeyDines Show: https://www.youtube.com/channel/UCxuvDkUxwEERVG9OZkxBtaA But Does It Djent: https://www.youtube.com/watch?v=5uD31YJkJj4 10 Styles Of Breakdowns: https://www.youtube.com/watch?v=7UPjLu5pHnE 10 styles of metal: https://www.youtube.com/watch?v=nKS1WTM6fzg 10 ways to hold a guitar: https://www.youtube.com/watch?v=v6hZ90IF0ps Things drummers say in the studio: https://www.youtube.com/watch?v=_2zUYmgIxEU Things cocky bassists say: https://www.youtube.com/watch?v=yG7H55V_4O0 Shred Wars: https://www.youtube.com/playlist?list=PLnOz4ii-wwznabw6cTyp4-ClLd68lJGjK Crazy Metal Facts: https://www.youtube.com/playlist?list=PLnOz4ii-wwzmPzHQW3hLlDR3qpugpaREf All Guitar Videos: https://www.youtube.com/playlist?list=PLnOz4ii-wwzlMlszfKXrFeWGpQDQEaUnk All Vocal Videos: https://www.youtube.com/playlist?list=PLnOz4ii-wwzkTSvE57jAWSLLuMa8hE58J All Drum Videos: https://www.youtube.com/playlist?list=PLnOz4ii-wwzkOZNm_towVRcEPsD7-dJqP Click the links below to stay connected! Thanks for the support! MERCH STORE: http://jareddines.bigcartel.com/ FACEBOOK: https://www.facebook.com/jared.dines INSTAGRAM: https://instagram.com/j4r3dd1n3s TWITTER: https://twitter.com/JaredDines MY BANDS MUSIC: https://dissimulator.bandcamp.com/ VIDEO SHOT/EDITED BY: http://www.caughtalivemedia.com/ -
 38:48
38:48Детский развлекательный центр Fancyfox / Fancyfox Children's entertainment center Fancyfox
Детский развлекательный центр Fancyfox / Fancyfox Children's entertainment center FancyfoxДетский развлекательный центр Fancyfox / Fancyfox Children's entertainment center Fancyfox
Детский развлекательный центр Fancyfox / Children's entertainment center Fancyfox https://goo.gl/IcRkmM Путилычи играют в детском развлекательном центре FancyFox. Играем в интерактивные автоматы в Фэнсифокс. Встречаем нашего подписчика в детском центре. Джунгли парк «FancyFox» – это развлекательный остров для детей и их родителей, где каждый визит – необычное, увлекательное путешествие в удивительный мир детства. Здесь не бывает скучно – Американская горка, Виртуальный 5Д Кинотеатр, карусель «Дикая Сельва», автодром, башня падения и самый большой детский лабиринт! Веселимся вместе! Вместе с «FancyFox» любой праздник становится ярче – день рождения, выпускной младших классов и детсадовцев, первый школьный звонок, Новый год и любая другая выдающаяся дата. Программа аниматоров, ростовых кукол подарит всем незабываемые впечатления. Это будет, несомненно лучший, Твой праздник! Джунгли парк «FancyFox» открыт каждый день с 10.00 до 22.00. Адрес: ТРЦ «Планета», 2 уровень. Телефон: 561-201 Веб-сайт:http://www.fancy-fox.ru Местоположение: ТРЦ Планета, 2 уровень, ул. ДОЗ 10 а, Новокузнецк Путилычи - семейный спортивно-развлекательный канал о взаимоотношениях, о здоровом образе жизни, спорте, единоборствах, совместных играх и соревнованиях! Занимайтесь со своими детишками интересными и веселыми вещами, ведь ДЕТИ - ЭТО СЧАСТЬЕ! _ Putilichy - family sports and entertainment channel about relationships, about healthy lifestyles, sports, martial arts, cooperative games and competitions! Engage with your kids interesting and fun things, because children - this is happiness! ___ Денис "Путилыч" - профиль вконтакте https://vk.com/putilich Группа канала в Вконтакте https://vk.com/Putilichy Мой профиль в ОК (Одноклассники) http://ok.ru/putilich Мой профиль в фэйсбук (Facebook) https://www.facebook.com/Putilich Мой профиль в Instagram https://www.instagram.com/putilich/ Музыкальный трек предоставлен VSP Group и Apollo Music с сайта музыкальной библиотеки http://www.findthetune.com Партнерская программа моего канала: https://youpartnerwsp.com/join?93044 -
 6:26
6:26Purple Rain by Bruce Springsteen Live 4/23/2016 Brooklyn Barclays Center
Purple Rain by Bruce Springsteen Live 4/23/2016 Brooklyn Barclays CenterPurple Rain by Bruce Springsteen Live 4/23/2016 Brooklyn Barclays Center
Purple Rain by Bruce Springsteen live 4/23/2016 Brooklyn Barclay Center -
 0:39
0:39Flagrante - Fazendo cavalo de pau no estacionamento de Shopping Center no Canadá
Flagrante - Fazendo cavalo de pau no estacionamento de Shopping Center no CanadáFlagrante - Fazendo cavalo de pau no estacionamento de Shopping Center no Canadá
INSCREVA-SE NO CANAL ► http://goo.gl/aBlST2 SITE ► http://www.canadadiario.com/ CAMISETAS DO DIMITRI ► http://dimitrikozma.spreadshirt.com/ FACEBOOK ► https://www.facebook.com/canadadiario INSTAGRAM ► https://instagram.com/canadadiario/ TWITTER ► https://twitter.com/CanadaDiario +++++++++++++++++++++++++++++++ Flagrante - Babaca fazendo cavalo de pau no estacionamento de Shopping Center no Canadá Gostou? Comente, dê seu "like", adicione este vídeo aos favoritos e divulgue nas mídias sociais, como Facebook e Twitter. ;-) ------------------------------------------------ 2015 08 03 -
 8:29
8:29Google Data Center 360° Tour
Google Data Center 360° TourGoogle Data Center 360° Tour
Take a Google data center tour in 360° -- brought to you by the Google Cloud Platform team. Learn about the massive scale, the incredible attention to security and privacy, and the amazing efforts to make the data center extremely efficient and green. How to view the 360° video: Desktop using Google Chrome: Use your mouse or trackpad to change your view while the video plays YouTube app on mobile: Move your device around to look at all angles while the video plays Google Cardboard: Load the video in the YouTube app and tap on the cardboard icon when the video starts to play. Insert your phone in cardboard and enjoy. Cardboard is currently only supported by the YouTube app on Android. iOS support is coming soon! Learn more about Google Cloud Platform -- https://cloud.google.com Google Cloud Platform Blog -- https://cloudplatform.googleblog.com/2016/03/Google-Data-Center-360-Tour.html Learn more about Google Data Centers -- http://www.google.com/about/datacenters Follow the Google Cloud Platform Developer Advocates -- https://twitter.com/googlecloud/lists... -
 0:28
0:28Donald Trump does Impression of Indian Call Center Worker
Donald Trump does Impression of Indian Call Center Worker -
 7:00
7:00Purple Rain - Bruce Springsteen - Barclay's Center - April 23, 2016 - Prince Tribute
Purple Rain - Bruce Springsteen - Barclay's Center - April 23, 2016 - Prince TributePurple Rain - Bruce Springsteen - Barclay's Center - April 23, 2016 - Prince Tribute
Bruce Springsteen and the E Street Band perform Purple Rain in honor of Prince. In Brooklyn at the Barclay's Center on April 23, 2016 -
 4:14
4:14Riesen Experiment 2 | Intelligente Knete, Schleim, Agua Sand, Jelly Beans, Center Shock in Essig
Riesen Experiment 2 | Intelligente Knete, Schleim, Agua Sand, Jelly Beans, Center Shock in EssigRiesen Experiment 2 | Intelligente Knete, Schleim, Agua Sand, Jelly Beans, Center Shock in Essig
Riesen Experiment 2 | Intelligente Knete, Schleim, Agua Sand, Jelly Beans, Center Shock in Essig ABONNIERT den Kanal kostenlos wenn Ihr Spielzeuge liebt: http://goo.gl/GpXJjY DAUMEN HOCH! -- wenn das Video Euch gefallen hat TEILT das Video mit Euren Freunden! https://www.youtube.com/user/SpieleSpielzeug Diese Playlists könnten Euch auch interessieren: Spielzeuge für Jungs: https://www.youtube.com/watch?v=R-iTUlicNXo&list;=PL_TZokecG1Co-XmBnHdyLY2m6jqnl5E8x Spielzeuge für Mädchen: https://www.youtube.com/watch?v=mIEVgegUQoY&list;=PL_TZokecG1CocOfYb-v0bv7QXwVd-Drw6 Play Doh Playlist: https://www.youtube.com/watch?v=R-iTUlicNXo&list;=PL_TZokecG1CpPYPEnLie1pSi1upJ5MnYK Loom Bands Unboxings: https://www.youtube.com/watch?v=3QxplB6eCNY&list;=PL_TZokecG1CpeAk7plrD2yHOnckpwc0eS Süßigkeiten aus Spielzeug: https://www.youtube.com/watch?v=fvJKh4HD6Uo&list;=PL_TZokecG1Cq485fP8-d29F2CwjD7ffyW Intelligente Knete: https://www.youtube.com/watch?v=PPwSKiedil4&list;=PL_TZokecG1Cr3C9K9hXZCv-ueSuNx4X-h Playmobil: https://www.youtube.com/watch?v=XpQ3X7VWWuw&list;=PL_TZokecG1CpcIUsxA0LV2m-xE578Ok05 Barbie und Puppen: https://www.youtube.com/watch?v=gFU6Y98IHus&list;=PL_TZokecG1Cpp_L6vuypTQLvo0yeAYW9g Lego: https://www.youtube.com/watch?v=6bHi31FPI8s&list;=PL_TZokecG1CrN_MVOnY3wt7gkxjm-3UMS Diese Kanäle könnten Euch auch interessieren: Lilli und Lars: https://www.youtube.com/channel/UC0074qE0PgLefqGnqN5QIfg ABC lernen: https://www.youtube.com/user/ABC123lernen DIY Inspiration Kids Club: https://www.youtube.com/channel/UCKe4uxgeC1LY61Ko9IYrYsQ DIY Ideen: https://www.youtube.com/user/DIYselbermachen Häkel-Ideen: https://www.youtube.com/user/TolleWolle24 DIY Inspiration Reviews: https://www.youtube.com/channel/UCuEU6QTnjdP9PiYhCxocHQQ DIY Inspiration Koch- und BackClub: https://www.youtube.com/channel/UCLI1DZEpS2PNfkfk9KEnUJw ----------------- Abonniert den Kanal und seit immer die ersten die über neue Videos informiert werden! Wir stellen täglich ein neues Spielzeugvideo vor! Unsere Zuschauer sind 2 bis 90 Jahr alt. Wenn Ihr kein Spielzeug Video mehr verpassen wollt, abonniert kostenlos den Kanal! Danke! http://www.youtube.com/user/SpieleSpielzeug?sub_confirmation=1 Viel Spass beim Zuschauen und Mitspielen! Musik aus YouTube Bibliothek BESUCHT UNS AUF FACEBOOK: https://www.facebook.com/pages/Spiel-mit-mir-Kinderspielzeuge/1471553083091700?fref=ts ------------- Play-Doh in anderen Sprachen: Playdough, Play-Doh, Clay, Plasticine, Plastilina, Plastiline, مادة لدائنية, 橡皮泥, 橡皮泥, pâte à modeler, プラスティシーン, plasticina, пластилин, modellera, пластилін, Crayola ------------- Disclaimer: Dieser YouTube Kanal ist unabhängig. LEGO®, PLAYMOBIL®, PLAY-DOH®, HOTWHEELS®, DISNEY®, TURTLES®, MY LITTLE PONY®, LALALOOPSY®, BARBIE® und alle anderen in diesem Kanal gezeigten Spielzeugmarken sind Marken der jeweiligen Hersteller, durch die der vorliegende YouTube Kanal weder gesponsert noch autorisiert oder unterstützt wird.
- Center of mass
- Center of symmetry
- Centre (geometry)
- Centre of mass
- Centroid
- Chebyshev center
- Circle
- Circumcentre
- Elementary geometry
- Ellipse
- Equilateral triangle
- Excentre
- Geometry
- Greek language
- Incentre
- Isometry group
- Nine-point centre
- Orthocentre
- Parallelogram
- Rectangle
- Rhombus
- Sphere
- Square (geometry)
- Symmetries
- Triangle center
- Triangle centre
- Trilinear coordinate
- Wikipedia INCITE
- Wikipedia Stub
- Archimedes
- Bernhard Riemann
- Carl Benjamin Boyer
- Carl Friedrich Gauss
- David Hilbert
- Edwin Abbott Abbott
- Euclid
- Eudoxus of Cnidus
- Felix Klein
- Gersonides
- Henri Poincaré
- Immanuel Kant
- Jeremy Gray
- John Wallis
- János Bolyai
- Leonhard Euler
- Nubia
- Omar Khayyám
- Pierre de Fermat
- René Descartes
- Sophus Lie
- Thales
- Thābit ibn Qurra
- Witelo
-

JOURNEY TO THE CENTER OF PLANET MINECRAFT!! | Terra Swoop Force Custom Map Adventure
JOURNEY TO THE CENTER OF PLANET MINECRAFT!! | Terra Swoop Force Custom Map Adventure Leave a like for Part 2 :D | Don't miss a vid! ►http://bit.ly/SubLog Support The Mapmakers! https://www.patreon.com/Noxcrew Terra Swoop Force is a team of scientists who have taken it upon themselves to harvest valuable minerals from the center of the Earth. A mission gone astray has left behind two scientists, and your job is to travel to the core of the planet and retrieve them. Are you up to the task!? _ ► Facebook http://facebook.com/Logdotzip ► Twitch http://twitch.tv/Logdotzip ► Twitter http://twitter.com/Logdotzip ► Instagram http://instagram.com/Logdotzip _ Minecraft Terra Swoop Force Map Download http://noxcrew.com/threads/terra-swoop-force-an-arcadey-minecraft-adventure-map-mc1-9-2.2773/ by No... -

-

JOURNEY TO THE CENTER OF THE EARTH IN MINECRAFT!
An amazing Minecraft Map with a Journey to the center of the Earth! My Gaming Channel: http://www.youtube.com/VikkstarPlays Follow me on TWITTER: http://twitter.com/#!/Vikkstar123 Like my Facebook Page: http://www.facebook.com/Vikkstar123 My Instagram: http://instagram.com/Vikkstagram The Pack: https://www.youtube.com/Lachlan https://www.youtube.com/PrestonPlayz https://www.youtube.com/MrWoofless https://www.youtube.com/JeromeASF https://www.youtube.com/TheBajanCanadian My Servers: http://treasurewars.net/ IP: treasurewars.net My capture card: http://e.lga.to/v Follow me on Twitch for Livestreams: http://www.twitch.tv/vikkstar123 Check out my other channels linked below: FPS & More: http://www.youtube.com/Vikkstar123 Lets Play: http://www.youtube.com/VikkstarPlays Map: http://noxcre... -

Heftiges Acer Event im World Trade Center!
Heute ging auf zum Acer Event, dass doch tatsächlich oben in einem der New-Yorker World-Trade-Center Türme stattgefunden hat! Was da so alles spannendes Vorgestellt wurde und noch viel mehr, seht ihr in diesem Vlog. Viel Spaß! Mein Reise-Vlog Setup: Kamera: http://amzn.to/1Xgp1qX Objektiv: http://amzn.to/1YkCTxc Mikrofon: http://amzn.to/1IFqmRq Stativ: http://amzn.to/1Xgp8Tb Actioncam: http://amzn.to/1jsccaB Rucksack: http://amzn.to/1N9yeqL Kann Spuren der Musik von www.epidemicsound.com, Music4Montage und The Passion Hifi enthalten ;) -------------------------------------------------------------- Twitter: http://www.twitter.com/felixba Facebook: http://www.facebook.com/felixbaTV Instagram: http://www.instagram.com/felixba Hauptkanal auf Youtube: http://www.youtube.com/felixba94 M... -

16 Secrets Call Center Employees Won’t Tell You
“The more upset you get, the funnier it is to me!” Check out more awesome videos at BuzzFeedVideo! http://bit.ly/YTbuzzfeedvideo MUSIC The Morning Show Licensed via Warner Chappell Production Music Inc. SFX provided by Audioblocks. (https://www.Audioblocks.com) Made by BFMP www.buzzfeed.com/videoteam + Rosa Pasquarella www.twitter.com/whatrosasaid Toni Del Sorbo https://www.facebook.com/tonidelsorbo/ Deyo Forteza Instagram: @le_deyo STILLS Business telephone with extensions on desk in office Hemera Technologies / Thinkstockphotos.com Film Footage courtesy of Shutterstock, Inc. Used with Permission BASED ON THIS BUZZFEED POST: http://www.buzzfeed.com/michaelblackmon/23-secrets-call-center-employees-wont-tell-you GET MORE BUZZFEED: www.buzzfeed.com/videoteam www.facebook.com/buzz... -

Donald Trump uses terrible Indian accent ,Trump: impersonates Indian call-center worker
Donald Trump uses terrible Indian accent ,Trump: impersonates Indian call-center worker trump indian accent,Donald trump indian accent,Indian Accent,fake Indian Accent,Trump uses fake Indian accent,impersonates Indian call-center worker,Indian call-center,Indian call-center worker,Donald Trump - American Politician,trump indiana,donald trump rally,gop polls,how old is donald trump,trump delegate,trump delegate count,trump,trump news,hillary clinton,bernie sanders,debate,president,trump,donald trump,trump india,india,trump call center -

Things guitar center employees say (BLOOPERS)
Watch some of my other videos: The DickeyDines Show: https://www.youtube.com/channel/UCxuvDkUxwEERVG9OZkxBtaA But Does It Djent: https://www.youtube.com/watch?v=5uD31YJkJj4 10 Styles Of Breakdowns: https://www.youtube.com/watch?v=7UPjLu5pHnE 10 styles of metal: https://www.youtube.com/watch?v=nKS1WTM6fzg 10 ways to hold a guitar: https://www.youtube.com/watch?v=v6hZ90IF0ps Things drummers say in the studio: https://www.youtube.com/watch?v=_2zUYmgIxEU Things cocky bassists say: https://www.youtube.com/watch?v=yG7H55V_4O0 Shred Wars: https://www.youtube.com/playlist?list=PLnOz4ii-wwznabw6cTyp4-ClLd68lJGjK Crazy Metal Facts: https://www.youtube.com/playlist?list=PLnOz4ii-wwzmPzHQW3hLlDR3qpugpaREf All Guitar Videos: https://www.youtube.com/playlist?list=PLnOz4ii-wwzlMlszfKXrFeWGpQDQE... -

Детский развлекательный центр Fancyfox / Fancyfox Children's entertainment center Fancyfox
Детский развлекательный центр Fancyfox / Children's entertainment center Fancyfox https://goo.gl/IcRkmM Путилычи играют в детском развлекательном центре FancyFox. Играем в интерактивные автоматы в Фэнсифокс. Встречаем нашего подписчика в детском центре. Джунгли парк «FancyFox» – это развлекательный остров для детей и их родителей, где каждый визит – необычное, увлекательное путешествие в удивительный мир детства. Здесь не бывает скучно – Американская горка, Виртуальный 5Д Кинотеатр, карусель «Дикая Сельва», автодром, башня падения и самый большой детский лабиринт! Веселимся вместе! Вместе с «FancyFox» любой праздник становится ярче – день рождения, выпускной младших классов и детсадовцев, первый школьный звонок, Новый год и любая другая выдающаяся дата. Программа аниматоров, ростовых ку... -

Purple Rain by Bruce Springsteen Live 4/23/2016 Brooklyn Barclays Center
Purple Rain by Bruce Springsteen live 4/23/2016 Brooklyn Barclay Center -

Flagrante - Fazendo cavalo de pau no estacionamento de Shopping Center no Canadá
INSCREVA-SE NO CANAL ► http://goo.gl/aBlST2 SITE ► http://www.canadadiario.com/ CAMISETAS DO DIMITRI ► http://dimitrikozma.spreadshirt.com/ FACEBOOK ► https://www.facebook.com/canadadiario INSTAGRAM ► https://instagram.com/canadadiario/ TWITTER ► https://twitter.com/CanadaDiario +++++++++++++++++++++++++++++++ Flagrante - Babaca fazendo cavalo de pau no estacionamento de Shopping Center no Canadá Gostou? Comente, dê seu "like", adicione este vídeo aos favoritos e divulgue nas mídias sociais, como Facebook e Twitter. ;-) ------------------------------------------------ 2015 08 03 -

Google Data Center 360° Tour
Take a Google data center tour in 360° -- brought to you by the Google Cloud Platform team. Learn about the massive scale, the incredible attention to security and privacy, and the amazing efforts to make the data center extremely efficient and green. How to view the 360° video: Desktop using Google Chrome: Use your mouse or trackpad to change your view while the video plays YouTube app on mobile: Move your device around to look at all angles while the video plays Google Cardboard: Load the video in the YouTube app and tap on the cardboard icon when the video starts to play. Insert your phone in cardboard and enjoy. Cardboard is currently only supported by the YouTube app on Android. iOS support is coming soon! Learn more about Google Cloud Platform -- https://cloud.google.com Goo... -

-

Purple Rain - Bruce Springsteen - Barclay's Center - April 23, 2016 - Prince Tribute
Bruce Springsteen and the E Street Band perform Purple Rain in honor of Prince. In Brooklyn at the Barclay's Center on April 23, 2016 -

Riesen Experiment 2 | Intelligente Knete, Schleim, Agua Sand, Jelly Beans, Center Shock in Essig
Riesen Experiment 2 | Intelligente Knete, Schleim, Agua Sand, Jelly Beans, Center Shock in Essig ABONNIERT den Kanal kostenlos wenn Ihr Spielzeuge liebt: http://goo.gl/GpXJjY DAUMEN HOCH! -- wenn das Video Euch gefallen hat TEILT das Video mit Euren Freunden! https://www.youtube.com/user/SpieleSpielzeug Diese Playlists könnten Euch auch interessieren: Spielzeuge für Jungs: https://www.youtube.com/watch?v=R-iTUlicNXo&list;=PL_TZokecG1Co-XmBnHdyLY2m6jqnl5E8x Spielzeuge für Mädchen: https://www.youtube.com/watch?v=mIEVgegUQoY&list;=PL_TZokecG1CocOfYb-v0bv7QXwVd-Drw6 Play Doh Playlist: https://www.youtube.com/watch?v=R-iTUlicNXo&list;=PL_TZokecG1CpPYPEnLie1pSi1upJ5MnYK Loom Bands Unboxings: https://www.youtube.com/watch?v=3QxplB6eCNY&list;=PL_TZokecG1CpeAk7plrD2yHOnckpwc0eS Süßigkeiten au... -

-

Youtuber Körperteile erraten | Center Shock Challenge mit mydealz
Schaffen wir es die Youtuber anhand ihrer Körperteile zu erraten? Als Bestrafung gibt es Center Shocks und ich verrate schonmal so viel: am Ende war es ganz schön SAUER! Hier gehts zur Pornotitel Challenge von Marvin: http://1.kleinaber.de/1MONbnY Hier kostenlos meinen Kanal Abonnieren: https://goo.gl/mpM6hb Mein 2. Kanal Hannah Kocht: https://goo.gl/sba3E9 Besucht mich auch auf meinem Blog: http://kleinaber.de Wenn euch die Challenge gefallen hat, lasst doch einen Daumen nach oben da :) Hier gehts zu Marvins Kanal: http://1.kleinaber.de/2175rve Instagram @KleinaberHannah Facebook.com/KleinaberHannah Twitter @KleinaberHannah Weil jetzt schon so oft danach gefragt wurde: Mein Objektiv*: http://amzn.to/1gFQxuc Mein Ton*: http://amzn.to/1NkJ4ym * Falls Ihr das Produkt über diesen Link... -

Aimpoint Sportsman Shooting Center Tour
Larry takes a tour of Aimpoint's Sportsman Shooting Center. A state of the art shooting cinema located in Grapevine Texas. -

Aretha Franklin (You Make Me Feel Like) A Natural Woman - Kennedy Center Honors 2015
Full segment of Aretha Franklin (You Make Me Feel Like) A Natural Woman - Kennedy Center Honors 2015. Chilina Kennedy, plays Carole King in Beautiful, the musical, introduces Aretha. -

Survei Populi Center: Pilgub DKI 2017, Kinerja Ahok Serta DPRD & Elektabilitas Cagub Lain
sumber: Populi Center Update Berita TyoJB Via: - Web: http://tyojb.blogspot.com - Twitter: https://twitter.com/Jokowi_JK_Ahok - Facebook: https://www.facebook.com/jokowi.jk.ahok Kritik & masukan ke admin TyoJB dapat disampaikan ke: - SMS: 082132588207 - Email: tyo.jakartabaru@gmail.com Untuk pengaduan warga kepada Pemprov DKI Jakarta dapat disampaikan melalui: - Facebook: https://www.facebook.com/infojakarta - Twitter: https://twitter.com/jakartagoid - SMS Center: 32881818 - Call Center: 164 - Email: sekretariat.gubdki@gmail.com - Website Lapor: https://www.lapor.go.id/ TOP 10 Video Terpopuler Bulan Ini: ** https://www.youtube.com/playlist?list=PL0m89HXXcIM83MFUIn3ie8fxn5bB3aK8T ** Menyuguhkan Update Berita Video Terbaru: Basuki TP (Ahok), Djarot Saiful & Seputar Ibukota Jakarta Ser... -

Clippers center DeAndre Jordan previews Game 4 against Blazers
The center said the defense must defend Portland's pick-and-rolls better, finishing off possessions and improve their defensive rebounding. -

Donald Trump impersonates Indian call center worker.
The Republican front-runner also said he once called a credit-card call center, suspecting the employees were working from India -

Inside a Google data center
Joe Kava, VP of Google's Data Center Operations, gives a tour inside a Google data center, and shares details about the security, sustainability and the core architecture of Google's infrastructure. -

Splashlings Medical Center Doctor & Nurse Exclusives + 6 Pack with Surprise Shell - Cookieswirlc
Unboxing the Splashlings Medical Center Playset were all the under sea friends come for a check up. Comes with 2 exclusives. Unboxing a 6 pack set with a mermaid and a surprise shell with a Splashling inside. Who will it be? - Watch my last video: https://www.youtube.com/watch?v=P3etj18TGCc - Hi Cookie fans, never miss one of my videos... SUBSCRIBE: http://bit.ly/1RYkDF6 More Videos: - DIY Squishy Cookie Nut Shopkins Season 4 Inspired Easy Craft Do It Yourself http://bit.ly/1RYl3eJ - Mega Littlest Pet Shop Collection Tour All Cats Dogs Fairy More Animals LPS Toys http://bit.ly/1TJfTIj - Splashlings Mermaid 12 Pack & Season 4 Shopkins 12 with Surprise Blind Bags http://bit.ly/25RWz04 🍪🍪🍪Find Me On My Official Social Media🍪🍪🍪 - Website and Blog: www.cookieswirlc.com - Instagram: ...
JOURNEY TO THE CENTER OF PLANET MINECRAFT!! | Terra Swoop Force Custom Map Adventure
- Order: Reorder
- Duration: 15:22
- Updated: 24 Apr 2016
- views: 3465
- published: 24 Apr 2016
- views: 3465
Things guitar center employees say
- Order: Reorder
- Duration: 7:52
- Updated: 18 Apr 2016
- views: 42002
JOURNEY TO THE CENTER OF THE EARTH IN MINECRAFT!
- Order: Reorder
- Duration: 25:09
- Updated: 25 Apr 2016
- views: 14208
- published: 25 Apr 2016
- views: 14208
Heftiges Acer Event im World Trade Center!
- Order: Reorder
- Duration: 14:33
- Updated: 25 Apr 2016
- views: 6405
- published: 25 Apr 2016
- views: 6405
16 Secrets Call Center Employees Won’t Tell You
- Order: Reorder
- Duration: 1:45
- Updated: 22 Apr 2016
- views: 103030
- published: 22 Apr 2016
- views: 103030
Donald Trump uses terrible Indian accent ,Trump: impersonates Indian call-center worker
- Order: Reorder
- Duration: 0:42
- Updated: 23 Apr 2016
- views: 202
- published: 23 Apr 2016
- views: 202
Things guitar center employees say (BLOOPERS)
- Order: Reorder
- Duration: 6:16
- Updated: 20 Apr 2016
- views: 21450
- published: 20 Apr 2016
- views: 21450
Детский развлекательный центр Fancyfox / Fancyfox Children's entertainment center Fancyfox
- Order: Reorder
- Duration: 38:48
- Updated: 25 Apr 2016
- views: 1153
- published: 25 Apr 2016
- views: 1153
Purple Rain by Bruce Springsteen Live 4/23/2016 Brooklyn Barclays Center
- Order: Reorder
- Duration: 6:26
- Updated: 24 Apr 2016
- views: 960
- published: 24 Apr 2016
- views: 960
Flagrante - Fazendo cavalo de pau no estacionamento de Shopping Center no Canadá
- Order: Reorder
- Duration: 0:39
- Updated: 25 Apr 2016
- views: 31
- published: 25 Apr 2016
- views: 31
Google Data Center 360° Tour
- Order: Reorder
- Duration: 8:29
- Updated: 23 Mar 2016
- views: 464
- published: 23 Mar 2016
- views: 464
Donald Trump does Impression of Indian Call Center Worker
- Order: Reorder
- Duration: 0:28
- Updated: 26 Apr 2016
- views: 14
Purple Rain - Bruce Springsteen - Barclay's Center - April 23, 2016 - Prince Tribute
- Order: Reorder
- Duration: 7:00
- Updated: 24 Apr 2016
- views: 165
- published: 24 Apr 2016
- views: 165
Riesen Experiment 2 | Intelligente Knete, Schleim, Agua Sand, Jelly Beans, Center Shock in Essig
- Order: Reorder
- Duration: 4:14
- Updated: 23 Apr 2016
- views: 930
- published: 23 Apr 2016
- views: 930
Ark: Survival Evolved - BEST BASE LOCATIONS THE CENTER!
- Order: Reorder
- Duration: 10:29
- Updated: 25 Apr 2016
- views: 378
Youtuber Körperteile erraten | Center Shock Challenge mit mydealz
- Order: Reorder
- Duration: 7:35
- Updated: 24 Apr 2016
- views: 10040
- published: 24 Apr 2016
- views: 10040
Aimpoint Sportsman Shooting Center Tour
- Order: Reorder
- Duration: 4:44
- Updated: 22 Apr 2016
- views: 5765
- published: 22 Apr 2016
- views: 5765
Aretha Franklin (You Make Me Feel Like) A Natural Woman - Kennedy Center Honors 2015
- Order: Reorder
- Duration: 5:04
- Updated: 31 Dec 2015
- views: 663335
- published: 31 Dec 2015
- views: 663335
Survei Populi Center: Pilgub DKI 2017, Kinerja Ahok Serta DPRD & Elektabilitas Cagub Lain
- Order: Reorder
- Duration: 10:03
- Updated: 25 Apr 2016
- views: 728
- published: 25 Apr 2016
- views: 728
Clippers center DeAndre Jordan previews Game 4 against Blazers
- Order: Reorder
- Duration: 2:27
- Updated: 25 Apr 2016
- views: 0
- published: 25 Apr 2016
- views: 0
Donald Trump impersonates Indian call center worker.
- Order: Reorder
- Duration: 0:28
- Updated: 23 Apr 2016
- views: 174
- published: 23 Apr 2016
- views: 174
Inside a Google data center
- Order: Reorder
- Duration: 5:28
- Updated: 17 Dec 2014
- views: 2082850
- published: 17 Dec 2014
- views: 2082850
Splashlings Medical Center Doctor & Nurse Exclusives + 6 Pack with Surprise Shell - Cookieswirlc
- Order: Reorder
- Duration: 9:59
- Updated: 11 Apr 2016
- views: 4372
- published: 11 Apr 2016
- views: 4372
-

Geometry Dash 2.1 SECRETS REVEALED! (Trailer Analysis and RELEASE DATE?!)
Geometry Dash 2.1 update trailer deep analysis. I think I've found some crazy information about the release date here. Second Channel ► https://www.youtube.com/channel/UCSnmEl_MrgcOKMfUQzzkWGQ/videos --CONTACT ME-- Subscribe to me! ► https://www.youtube.com/channel/UC_BXQNOzX7ALIf8FkDqOahQ?sub_confirmation=1 Facebook ► https://www.facebook.com/EricVanWilderman/ Twitter ► https://twitter.com/VanWilderman Outro Song ► https://www.youtube.com/watch?v=KCoCY5QsfCU -

INFINITE GEOMETRY DASH LEVEL - Timeless by Cyrillic
Someone finally made it.. Probably infinite level.. Also I've seen someone on the forums that you can't beat it with the hack that makes you go to the end of the level, don't know if that's true. And from the comments I guess it crashes mobile... But yeah cool (I guess) level lol... ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ 👉 WANT TO DONATE? ●Donate link - https://goo.gl/jiqfps ●If you're enjoying my videos, you can donate, I'm not forcing of course, but it would really help me a lot, thanks if you do, any amount is appreciated. ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ 👉 Random Playlists ●Fun Facts About Geometry Dash - https://goo.gl/OpXN3L ●Dumb Comments On GD Vids - https://goo.gl/w6XxR7 ●Exposals - https://goo.gl/NZflhP ●Top 5-10 Lists - https://goo.gl/2kWUGL ●Hackers get featured levels - https://goo.gl/... -

Geometry Dash Update 2.1 Sneak Peek
Update 2.1 sneak peek! Thank you all for 1 million subscribers, you're awesome! :) Song: Fingerbang by MDK https://www.youtube.com/watch?v=BuPmq7yjDnI Get Geometry Dash here: iOS: https://itunes.apple.com/us/app/geometry-dash/id625334537 Google Play: https://play.google.com/store/apps/details?id=com.robtopx.geometryjump Steam: http://store.steampowered.com/app/322170 Follow for more info: https://www.facebook.com/geometrydash https://twitter.com/robtopgames -

-

Basic geometry: language and labels | Introduction to Euclidean geometry | Geometry | Khan Academy
Before learning any new concept (mathematical or otherwise), it's important we learn and use a common language and label concepts consistently. Watch the next lesson: https://www.khanacademy.org/math/geometry/intro_euclid/v/lines-line-segments-and-rays?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Missed the previous lesson? https://www.khanacademy.org/math/geometry/intro_euclid/v/euclid-as-the-father-of-geometry?utm_source=YT&utm;_medium=Desc&utm;_campaign=Geometry Geometry on Khan Academy: We are surrounded by space. And that space contains lots of things. And these things have shapes. In geometry we are concerned with the nature of these shapes, how we define them, and what they teach us about the world at large--from math to architecture to biology to astronomy (and everything ... -

NINE CIRCLES SUNSET! Geometry Dash [2.0] (Demon) - AnotherCircles by Zyzyx | GuitarHeroStyles
● Juegos Baratos con el código de descuento "GHERO"! https://www.g2a.com/r/advystyles ● Camisetas con un 20% de descuento con el código "GUITAR1"! http://www.pampling.com/ ★ DARKNESS INCOMING! (Info) https://www.youtube.com/watch?v=EcOWC4RRqn4 ★ DEM TRAVEL! https://www.youtube.com/watch?v=jktF8n3KoKY ➚ ID: 14309230 ➚ Demon Difficulty: 3/10 (Easy Demon) ► Sígueme! • Suscríbete al canal! ❱ https://www.youtube.com/user/GuitarHeroStyles?sub_confirmation=1 • Twitter! ❱ https://twitter.com/AdvyStyles • Mi canal de Twitch! ❱ http://www.twitch.tv/guitarherostyles • Facebook! ❱ https://www.facebook.com/GuitarHeroStyles • Instagram! ❱ https://instagram.com/advystyles ► Playlists! • Mis mayores logros! ❱ https://www.youtube.com/playlist?list=PLxNqK_fPi9KzkmUM-XyC-LmtK-XxDmW5b • Geometry Dash 2.1!... -

FREE STARS #10 | Geometry Dash
. More free stars - https://goo.gl/zlP2o9 ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ 👉 WANT TO DONATE? ●Donate link - https://goo.gl/jiqfps ●If you're enjoying my videos, you can donate, I'm not forcing of course, but it would really help me a lot, thanks if you do, any amount is appreciated. ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ 👉 Random Playlists ●Fun Facts About Geometry Dash - https://goo.gl/OpXN3L ●Dumb Comments On GD Vids - https://goo.gl/w6XxR7 ●Exposals - https://goo.gl/NZflhP ●Top 5-10 Lists - https://goo.gl/2kWUGL ●Hackers get featured levels - https://goo.gl/tNq8jk ●Geometry Dash 2.1 Stuff - https://goo.gl/sYU4UZ ●Geometry Dash Texture Packs - https://goo.gl/G2t6Vo ●Geometry Dash Drama - https://goo.gl/nNhdsz ●Geometry Dash Comedy News - https://goo.gl/bdWBsY ●Not Patched Secret Way Demons - http... -

Geometry Dash - SILENT SKRILLEX - Impossible (Semi-AV)
//- Geometry Dash (Song: My Name Is Skrillex (REMIX) BY CETHIC) Want more impossible levels soon? Lemme know in the comment section. Done with start positions and semi-av (semi-av = half-autoversion). Thanks for watching. Thumbnail made by [DW] Hydro cuz I had no time atm. Thanks bud. https://www.youtube.com/channel/UCr9138Ti9s3xgubpilujRnA ──────────────────── FOLLOW ME ON SOCIAL MEDIA; • TWITTER (New) ➚ https://twitter.com/ToshDeluxe • Follow me on Instagram ➚ @toshey https://instagram.com/toshey • TWITCH ➚ http://www.twitch.tv/toshdeluxe • SNAPCHAT ➚ WhiteAgeRose ──────────────────── //- PC Specifications -OS: Windows 8.1 x64 -Case: Sharkoon VG5-W - Red -CPU: Intel® Core™ i7-6700K -CPU Speed: @ 4.0 GHz -Cooler: Water Cooling Corsair Hydro H100i GTX -MB: MSI B150M BAZOOKA -GPU: NVIDIA... -

GEOMETRY DASH 2.1 REVIEW - Sneak Peek - MiKha
⚫ JUEGOS MUY BARATOS USANDO EL CÓDIGO "MIKA": https://www.g2a.com/r/mikha ⚫ SUSCRÍBETE ES GRATIS: http://bit.ly/1PZTuAS ⚫ TWITTER: https://twitter.com/XxMiKhaxX ►CANAL SECUNDARIO: https://www.youtube.com/user/MiKhaKiLLeR ••••LISTAS DE REPRODUCCIÓN•••• ► Niveles Épicos: http://bit.ly/1H46Gkj ► Estrellas Gratis En Geometry Dash: http://bit.ly/1H4742g ► Detalles Sobre Actualizaciones Y Secretos: http://bit.ly/1I22QsW ► Tops 5 En Geometry Dash: http://bit.ly/1LWJSra ► Demons: http://bit.ly/22xcDTs ❤ MIS REDES SOCIALES ❤ ►Instagram: https://www.instagram.com/bymikhaxx/ ►Twitter: https://twitter.com/XxMiKhaxX ►Twitch: http://www.twitch.tv/bymikha ►Facebook: https://www.facebook.com/MiKhaXx ►Google +: http://bit.ly/196BFAZ ☢ τσdσs lσs Dεяεcнσs яεsεяvαdσs® ☢ -

TOP 5 NIVELES DE GEOMETRY DASH 2.1 - MiKha
❤ ¿LLEGAMOS A 3.000 LÍKES PARA MÁS TOPS 5? ❤ ⚫ SUSCRÍBETE ES GRATIS: http://bit.ly/1PZTuAS ⚫ TWITTER: https://twitter.com/XxMiKhaxX Para jugar al nivel del puesto Nº 1 y 2 es necesario descargar el Texture Pack de GDL7u7: https://youtu.be/5sn5hFGOV3A ►CANAL SECUNDARIO: https://www.youtube.com/user/MiKhaKiLLeR ••••LISTAS DE REPRODUCCIÓN•••• ► Niveles Épicos: http://bit.ly/1H46Gkj ► Estrellas Gratis En Geometry Dash: http://bit.ly/1H4742g ► Detalles Sobre Actualizaciones Y Secretos: http://bit.ly/1I22QsW ► Tops 5 En Geometry Dash: http://bit.ly/1LWJSra ► Demons: http://bit.ly/22xcDTs ❤ MIS REDES SOCIALES ❤ ►Instagram: https://www.instagram.com/bymikhaxx/ ►Twitter: https://twitter.com/XxMiKhaxX ►Twitch: http://www.twitch.tv/bymikha ►Facebook: https://www.facebook.com/MiKhaXx ►Google ... -

Journey by lSkyJax (& Kronos) | Geometry Dash
beautiful art. unfortunately there is a lack of gameplay though. -

The Sacred Geometry of The Universe
According to Stephen Skinner, the study of sacred geometry has its roots in the study of nature, and the mathematical principles at work therein. Many forms observed in nature can be related to geometry, for example, the chambered nautilus grows at a constant rate and so its shell forms a logarithmic spiral to accommodate that growth without changing shape. Also, honeybees construct hexagonal cells to hold their honey. These and other correspondences are sometimes interpreted in terms of sacred geometry and considered to be further proof of the natural significance of geometric forms. If you want more videos like this, follow us on: * Twitter: http://www.twitter.com/ConspiraciesYT * Google+: http://www.google.com/+WhatTheyDontWantYouToKnow * Facebook: http://www.facebook.com/whattheydontw... -

When You're Bored playing Geometry Dash for Today.
Already completed the level by now. ( ͡° ͜ʖ ͡°) Only took me 97 attempts. ( ͡° ͜ʖ ͡°) This happens when you aren't concentrating. ( ͡° ͜ ͡°) Dat hard volume at the end tho. ͡° ͜ ͡° -

-

Geometry Dash (DEMON) - Clutterfunk V2 - by IIINeptuneIII
Old video (I know, bad audio). All song credits goes to Waterflame. Song: Waterflame - Clutterfunk Waterflame's channel: https://www.youtube.com/user/waterflame89 Clutterfunk song (by Waterflame): https://www.youtube.com/watch?v=D5uJOpItgNg ──────────────────── FOLLOW ME ON SOCIAL MEDIA; • TWITTER (New) ➚ https://twitter.com/ToshDeluxe • Follow me on Instagram ➚ @toshey https://instagram.com/toshey • TWITCH ➚ http://www.twitch.tv/toshdeluxe • SNAPCHAT ➚ WhiteAgeRose ──────────────────── //- PC Specifications -OS: Windows 8.1 x64 -Case: Sharkoon VG5-W - Red -CPU: Intel® Core™ i7-6700K -CPU Speed: @ 4.0 GHz -Cooler: Water Cooling Corsair Hydro H100i GTX -MB: MSI B150M BAZOOKA -GPU: NVIDIA GTX 980 4GB -RAM: Crucial Ballistix 16GB DDR4-2400 -HDD: 2000 GB HDD Sata III -Monitor: LG 25UM65-P... -

EL RAP DE FERNANFLOO EN GEOMETRY DASH 2.0
Canal de creador del vídeo: https://www.youtube.com/channel/UC4WMhrA676vJbKBx_zUFbNg -

Geometry Dash #29 - Самые непризнанные уровни
Если тебе понравилось видео - поставь пожалуйста лайк :) Группа ВК - http://vk.com/rekvizit8bit Стримы тут - http://www.twitch.tv/rekvizit8bit -

BLOODBATH WTF?! ~ Geometry Dash EricVanWilderman FAN-MADE Levels (6)
Geometry Dash MORE EricVanWilderman fan-made levels. Somebody snuck Bloodbath in there ;( Second Channel ► https://www.youtube.com/channel/UCSnmEl_MrgcOKMfUQzzkWGQ/videos --CONTACT ME-- Subscribe to me! ► https://www.youtube.com/channel/UC_BXQNOzX7ALIf8FkDqOahQ?sub_confirmation=1 Facebook ► https://www.facebook.com/EricVanWilderman/ Twitter ► https://twitter.com/VanWilderman Outro Song ► https://www.youtube.com/watch?v=KCoCY5QsfCU --OTHER LEVELS-- ToE2 v2 ► https://www.youtube.com/watch?v=8SsGpZ691Bk Deadlocked ► https://www.youtube.com/watch?v=z1rW1hwEV7k Reanimation ►https://www.youtube.com/watch?v=Vn8YBAe32kw X ► https://www.youtube.com/watch?v=vp52E3aqrds Blue Hell ► https://www.youtube.com/watch?v=NUP9JBPmQXc -

WIZWARD BOSS BATTLE - Geometry Dash
Defending my wizward title in Geometry Dash! Game Link: http://store.steampowered.com/app/322170/ Merch: http://mattshea.fanfiber.com Instagram: http://instagram.com/mattsheatv Reddit: http://reddit.com/r/mattshea Twitch: http://twitch.tv/mattshea Twitter: http://twitter.com/mattshea Facebook: http://facebook.com/mattsheatv -

EPIC MEGACOLLAB! Drowning [DEMON] by HexagonDashers | Geometry Dash
An epic megacollab by a French collab group, The Hexagon Dashers. It's really fun and I love the song! ------- ID: 18450970 Rate: 10* Difficulty: 3/10 (Easy Demon) ------ ✓✓ FOLLOW ME ON SOCIAL NETWORKS ✓✓ ♥ INSTAGRAM ♥ http://bit.ly/1XttfHo ♠ SOUNDCLOUD ♠ http://bit.ly/1nMlLD9 ♠ TWITTER ♠ https://twitter.com/demongmd ♠♠ SUPPORT ON PATREON ♠♠ https://www.patreon.com/gdandromeda?ty=h Intro music: Oliver Heldens - Shades of Grey (Ephwurd Future House Remix) Level Song: Omnivore - Drowning --- if you read down this far, comment 'ok' -

I'M HAVING A MELTDOWN! | Geometry Dash Meltdown
A whole new Geometry Dash means a whole lot of new ways to pull out my hair! Paint The Town Red ► https://www.youtube.com/watch?v=jVfUEP7op50 ►Twitter : https://twitter.com/Jack_Septic_Eye ►Instagram: http://instagram.com/jacksepticeye ►Facebook : https://facebook.com/officialjacksepticeye ►Merchandise: http://jacksepticeye.fanfiber.com/ Outro animation created by Cranbersher: https://www.youtube.com/user/Cranbersher Outro Song created by "Teknoaxe". It's called "I'm everywhere" and you can listen to it here http://www.youtube.com/watch?v=JPtNBwMIQ9Q -

Geometry Dash 2.0/Level 20 - Deadlocked
Really fun new demon with moving objects and teleports as well . I rate ez/medium demon :D Win sound - San Andreas Mission passed Menu music - K-391 - Electro House 2012 -

NEW ICON - Geometry Dash 2.1 News
bg song - https://goo.gl/1LMylU link - http://www.boomlings.com/images/brainy.png ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ 👉 WANT TO DONATE? ●Donate link - https://goo.gl/jiqfps ●If you're enjoying my videos, you can donate, I'm not forcing of course, but it would really help me a lot, thanks if you do, any amount is appreciated. ▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬ 👉 Random Playlists ●Fun Facts About Geometry Dash - https://goo.gl/OpXN3L ●Dumb Comments On GD Vids - https://goo.gl/w6XxR7 ●Exposals - https://goo.gl/NZflhP ●Top 5-10 Lists - https://goo.gl/2kWUGL ●Hackers get featured levels - https://goo.gl/tNq8jk ●Geometry Dash 2.1 Stuff - https://goo.gl/sYU4UZ ●Geometry Dash Texture Packs - https://goo.gl/G2t6Vo ●Geometry Dash Drama - https://goo.gl/nNhdsz ●Geometry Dash Comedy News - https://goo.gl/bdWB...
Geometry Dash 2.1 SECRETS REVEALED! (Trailer Analysis and RELEASE DATE?!)
- Order: Reorder
- Duration: 3:47
- Updated: 26 Apr 2016
- views: 4288
- published: 26 Apr 2016
- views: 4288
INFINITE GEOMETRY DASH LEVEL - Timeless by Cyrillic
- Order: Reorder
- Duration: 2:46
- Updated: 25 Apr 2016
- views: 2556
- published: 25 Apr 2016
- views: 2556
Geometry Dash Update 2.1 Sneak Peek
- Order: Reorder
- Duration: 0:38
- Updated: 16 Apr 2016
- views: 73662
- published: 16 Apr 2016
- views: 73662
Introduction to Geometry (1.1)
- Order: Reorder
- Duration: 14:32
- Updated: 31 Aug 2012
- views: 110543
Basic geometry: language and labels | Introduction to Euclidean geometry | Geometry | Khan Academy
- Order: Reorder
- Duration: 12:58
- Updated: 28 Feb 2012
- views: 589477
- published: 28 Feb 2012
- views: 589477
NINE CIRCLES SUNSET! Geometry Dash [2.0] (Demon) - AnotherCircles by Zyzyx | GuitarHeroStyles
- Order: Reorder
- Duration: 1:45
- Updated: 25 Apr 2016
- views: 40210
- published: 25 Apr 2016
- views: 40210
FREE STARS #10 | Geometry Dash
- Order: Reorder
- Duration: 2:30
- Updated: 26 Apr 2016
- views: 984
- published: 26 Apr 2016
- views: 984
Geometry Dash - SILENT SKRILLEX - Impossible (Semi-AV)
- Order: Reorder
- Duration: 1:26
- Updated: 23 Apr 2016
- views: 4320
- published: 23 Apr 2016
- views: 4320
GEOMETRY DASH 2.1 REVIEW - Sneak Peek - MiKha
- Order: Reorder
- Duration: 5:47
- Updated: 22 Apr 2016
- views: 7962
- published: 22 Apr 2016
- views: 7962
TOP 5 NIVELES DE GEOMETRY DASH 2.1 - MiKha
- Order: Reorder
- Duration: 6:14
- Updated: 25 Apr 2016
- views: 31975
- published: 25 Apr 2016
- views: 31975
Journey by lSkyJax (& Kronos) | Geometry Dash
- Order: Reorder
- Duration: 1:07
- Updated: 26 Apr 2016
- views: 942
- published: 26 Apr 2016
- views: 942
The Sacred Geometry of The Universe
- Order: Reorder
- Duration: 106:47
- Updated: 01 Feb 2015
- views: 349654
- published: 01 Feb 2015
- views: 349654
When You're Bored playing Geometry Dash for Today.
- Order: Reorder
- Duration: 1:37
- Updated: 25 Apr 2016
- views: 5924
- published: 25 Apr 2016
- views: 5924
Geometry Activities - MathHelp.com - 1000+ Online Math Lessons
- Order: Reorder
- Duration: 3:32
- Updated: 30 Sep 2008
- views: 121329
Geometry Dash (DEMON) - Clutterfunk V2 - by IIINeptuneIII
- Order: Reorder
- Duration: 2:08
- Updated: 25 Apr 2016
- views: 2280
- published: 25 Apr 2016
- views: 2280
EL RAP DE FERNANFLOO EN GEOMETRY DASH 2.0
- Order: Reorder
- Duration: 2:49
- Updated: 23 Apr 2016
- views: 6121
- published: 23 Apr 2016
- views: 6121
Geometry Dash #29 - Самые непризнанные уровни
- Order: Reorder
- Duration: 17:12
- Updated: 26 Apr 2016
- views: 5166
- published: 26 Apr 2016
- views: 5166
BLOODBATH WTF?! ~ Geometry Dash EricVanWilderman FAN-MADE Levels (6)
- Order: Reorder
- Duration: 28:23
- Updated: 24 Apr 2016
- views: 5224
- published: 24 Apr 2016
- views: 5224
WIZWARD BOSS BATTLE - Geometry Dash
- Order: Reorder
- Duration: 17:02
- Updated: 17 Apr 2016
- views: 51075
- published: 17 Apr 2016
- views: 51075
EPIC MEGACOLLAB! Drowning [DEMON] by HexagonDashers | Geometry Dash
- Order: Reorder
- Duration: 2:41
- Updated: 24 Apr 2016
- views: 5504
- published: 24 Apr 2016
- views: 5504
I'M HAVING A MELTDOWN! | Geometry Dash Meltdown
- Order: Reorder
- Duration: 15:10
- Updated: 30 Dec 2015
- views: 1740813
- published: 30 Dec 2015
- views: 1740813
Geometry Dash 2.0/Level 20 - Deadlocked
- Order: Reorder
- Duration: 2:06
- Updated: 27 Aug 2015
- views: 4721447
- published: 27 Aug 2015
- views: 4721447
NEW ICON - Geometry Dash 2.1 News
- Order: Reorder
- Duration: 0:35
- Updated: 24 Apr 2016
- views: 1710
- published: 24 Apr 2016
- views: 1710
- Playlist
- Chat
- Playlist
- Chat

JOURNEY TO THE CENTER OF PLANET MINECRAFT!! | Terra Swoop Force Custom Map Adventure
- Report rights infringement
- published: 24 Apr 2016
- views: 3465

Things guitar center employees say
- Report rights infringement
- published: 18 Apr 2016
- views: 42002

JOURNEY TO THE CENTER OF THE EARTH IN MINECRAFT!
- Report rights infringement
- published: 25 Apr 2016
- views: 14208

Heftiges Acer Event im World Trade Center!
- Report rights infringement
- published: 25 Apr 2016
- views: 6405

16 Secrets Call Center Employees Won’t Tell You
- Report rights infringement
- published: 22 Apr 2016
- views: 103030

Donald Trump uses terrible Indian accent ,Trump: impersonates Indian call-center worker
- Report rights infringement
- published: 23 Apr 2016
- views: 202

Things guitar center employees say (BLOOPERS)
- Report rights infringement
- published: 20 Apr 2016
- views: 21450

Детский развлекательный центр Fancyfox / Fancyfox Children's entertainment center Fancyfox
- Report rights infringement
- published: 25 Apr 2016
- views: 1153

Purple Rain by Bruce Springsteen Live 4/23/2016 Brooklyn Barclays Center
- Report rights infringement
- published: 24 Apr 2016
- views: 960

Flagrante - Fazendo cavalo de pau no estacionamento de Shopping Center no Canadá
- Report rights infringement
- published: 25 Apr 2016
- views: 31

Google Data Center 360° Tour
- Report rights infringement
- published: 23 Mar 2016
- views: 464

Donald Trump does Impression of Indian Call Center Worker
- Report rights infringement
- published: 26 Apr 2016
- views: 14

Purple Rain - Bruce Springsteen - Barclay's Center - April 23, 2016 - Prince Tribute
- Report rights infringement
- published: 24 Apr 2016
- views: 165

Riesen Experiment 2 | Intelligente Knete, Schleim, Agua Sand, Jelly Beans, Center Shock in Essig
- Report rights infringement
- published: 23 Apr 2016
- views: 930
- Playlist
- Chat

Geometry Dash 2.1 SECRETS REVEALED! (Trailer Analysis and RELEASE DATE?!)
- Report rights infringement
- published: 26 Apr 2016
- views: 4288

INFINITE GEOMETRY DASH LEVEL - Timeless by Cyrillic
- Report rights infringement
- published: 25 Apr 2016
- views: 2556

Geometry Dash Update 2.1 Sneak Peek
- Report rights infringement
- published: 16 Apr 2016
- views: 73662


Basic geometry: language and labels | Introduction to Euclidean geometry | Geometry | Khan Academy
- Report rights infringement
- published: 28 Feb 2012
- views: 589477

NINE CIRCLES SUNSET! Geometry Dash [2.0] (Demon) - AnotherCircles by Zyzyx | GuitarHeroStyles
- Report rights infringement
- published: 25 Apr 2016
- views: 40210

FREE STARS #10 | Geometry Dash
- Report rights infringement
- published: 26 Apr 2016
- views: 984

Geometry Dash - SILENT SKRILLEX - Impossible (Semi-AV)
- Report rights infringement
- published: 23 Apr 2016
- views: 4320

GEOMETRY DASH 2.1 REVIEW - Sneak Peek - MiKha
- Report rights infringement
- published: 22 Apr 2016
- views: 7962

TOP 5 NIVELES DE GEOMETRY DASH 2.1 - MiKha
- Report rights infringement
- published: 25 Apr 2016
- views: 31975

Journey by lSkyJax (& Kronos) | Geometry Dash
- Report rights infringement
- published: 26 Apr 2016
- views: 942

The Sacred Geometry of The Universe
- Report rights infringement
- published: 01 Feb 2015
- views: 349654

When You're Bored playing Geometry Dash for Today.
- Report rights infringement
- published: 25 Apr 2016
- views: 5924

Geometry Activities - MathHelp.com - 1000+ Online Math Lessons
- Report rights infringement
- published: 30 Sep 2008
- views: 121329
Scientists: Massive Subterranean Lakes, Channels Found Beneath Antarctic Glaciers
Edit WorldNews.com 26 Apr 2016Trump's big night: Front-runner sweeps 5 states in Northeast
Edit The Associated Press 27 Apr 2016No Need To Panic, But Your Facebook Account Has Been Hacked For A Good Reason
Edit WorldNews.com 26 Apr 2016Al-Qaida Claims Responsibility In Slaying Of Gay Activist, Friend In Bangladesh
Edit WorldNews.com 26 Apr 2016ISIS's Multimillion-Dollar Oil Deals With Assad Regime Uncovered in U.S. Special Forces Raid
Edit Newsweek 26 Apr 2016The top iPhone and iPad apps on App Store
Edit Times Union 27 Apr 2016Compatible Sparse Representation for Manifold Surfaces Developed (University of Science and Technology of China)
Edit Public Technologies 27 Apr 2016New climate science centre doesn’t make up for CSIRO cuts: experts (UNSW - The University of New South Wales)
Edit Public Technologies 27 Apr 2016MLB college opens centre for space studies
Edit The Times of India 27 Apr 2016Magadh varsity Vice Chancellor reviews arrangements for evaluation
Edit The Times of India 27 Apr 2016The order to end Manus detention was predictable. The next step is not
Edit The Guardian 27 Apr 2016Media Release - New Cultural Centre project to deliver a fresh collaborative approach to community & visitor services (Blayney Shire Council)
Edit Public Technologies 27 Apr 2016Manus Island detention centre to close, PNG Prime Minister says following court bombshell
Edit Sydney Morning Herald 27 Apr 2016New Canberra visitor centre at Regatta Point to open mid-year
Edit Sydney Morning Herald 27 Apr 2016Solar savings for Concord Centre for Mental Health (Sydney Local Health District)
Edit Public Technologies 27 Apr 2016Law ministry blocks HRD proposal to amend IIT Act
Edit Indian Express 27 Apr 2016Broadspectrum investors dump Ferrovial bid as stock falls
Edit Sydney Morning Herald 27 Apr 2016- 1
- 2
- 3
- 4
- 5
- Next page »







