- published: 09 Apr 2016
- views: 7076863
-
remove the playlistAleph Number
- remove the playlistAleph Number
- published: 06 Jul 2012
- views: 4743541
- published: 30 Nov 2015
- views: 437
- published: 22 Jan 2016
- views: 43
- published: 14 Sep 2008
- views: 12360
- published: 13 Dec 2011
- views: 6415
- published: 04 Oct 2015
- views: 1352

Aleph number
In mathematics, and in particular set theory, the aleph numbers are a sequence of numbers used to represent the cardinality (or size) of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph (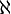 ) (though in older mathematics books the letter aleph is often printed upside down by accident, partly because a Monotype matrix for aleph was mistakenly constructed the wrong way up ).
) (though in older mathematics books the letter aleph is often printed upside down by accident, partly because a Monotype matrix for aleph was mistakenly constructed the wrong way up ).
The cardinality of the natural numbers is  (read aleph-naught or aleph-zero; the German term aleph-null is also sometimes used), the next larger cardinality is aleph-one
(read aleph-naught or aleph-zero; the German term aleph-null is also sometimes used), the next larger cardinality is aleph-one 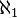 , then
, then  and so on. Continuing in this manner, it is possible to define a cardinal number
and so on. Continuing in this manner, it is possible to define a cardinal number  for every ordinal number α, as described below.
for every ordinal number α, as described below.
The concept goes back to Georg Cantor, who defined the notion of cardinality and realized that infinite sets can have different cardinalities.
The aleph numbers differ from the infinity (∞) commonly found in algebra and calculus. Alephs measure the sizes of sets; infinity, on the other hand, is commonly defined as an extreme limit of the real number line (applied to a function or sequence that "diverges to infinity" or "increases without bound"), or an extreme point of the extended real number line.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...

-
 23:46
23:46How To Count Past Infinity
How To Count Past InfinityHow To Count Past Infinity
Vote for Vsauce in the WEBBYS! https://pv.webbyawards.com/2016/online-film-video/video-channels-and-networks/science-education Sources and links to learn more below! I’m very grateful to mathematician Hugh Woodin, Professor of Philosophy and Mathematics at Harvard, for taking the time on multiple occasions to discuss this topic with me and help me wrap my (finite) head around it. I’m also grateful to David Eisenbud, the Director of the Mathematical Sciences Research Institute (MSRI) and professor of mathematics at the University of California, Berkeley, for his help and for connecting me with Hugh Woodin. And of course, big thanks to Brady Haran who created the “mile of pi” seen in this video and connected me with all these mathematicians in the first place. His channel, Numberphile, is superb: https://www.youtube.com/user/numberphile BOOKS related to these topics that I used: “The Outer Limits of Reason” by Noson S. Yanofsky: http://amzn.com/0262019353 “Infinity and The Mind” by Rudy Rucker: http://amzn.com/0691121273 “Roads to Infinity” by John C. Stilwell: http://amzn.com/1568814666 “More Precisely: The Math You Need to Do Philosophy” by Eric Steinhart: http://amzn.com/1551119099 “Satan, Cantor and Infinity: Mind-Boggling Puzzles” by Raymond M. Smullyan: http://amzn.com/0486470369 classic book that helps introduce concept of axioms: “Introduction to the Foundations of Mathematics” by Raymond L. Wilder: http://amzn.com/0486488209 Hugh Woodin speaking about infinity at the World Science Festival: https://youtu.be/KDCJZ81PwVM?t=29m45s Names of large (finite) numbers: https://en.wikipedia.org/wiki/Names_of_large_numbers Geoglyphs: The biggest number: https://goo.gl/maps/7GWcpnzo7iG2 Fovant badges: https://en.wikipedia.org/wiki/Fovant_Badges Battalion Park: https://en.wikipedia.org/wiki/Battalion_Park A mile of pi [VIDEO]: https://www.youtube.com/watch?v=0r3cEKZiLmg Wikipedia’s great visualization of ordinals out to omega^omega: https://en.wikipedia.org/wiki/File:Omega-exp-omega-labeled.svg as seen on: https://en.wikipedia.org/wiki/Ordinal_number this is also a good page about ordinals: http://math.wikia.com/wiki/Ordinal_Number also: http://www.cut-the-knot.org/WhatIs/Infinity/Ordinals.shtml and: https://en.wikipedia.org/wiki/Order_type and https://en.wikipedia.org/wiki/Well-order Axioms: https://en.wikipedia.org/wiki/Axiom https://www.reddit.com/r/askscience/comments/30xokb/have_there_been_axioms_that_later_have_been/ http://philosophy.stackexchange.com/questions/5922/what-is-the-difference-between-dogma-and-an-axiom http://www.cs.umd.edu/~gasarch/BLOGPAPERS/belaxioms1.pdf http://www.cs.umd.edu/~gasarch/BLOGPAPERS/belaxioms2.pdf THE UNREASONABLE EFFECTIVENSS OF MATHEMATICS IN THE NATURAL SCIENCES [PDF]: http://www.maths.ed.ac.uk/~aar/papers/wigner.pdf https://en.wikipedia.org/wiki/The_Unreasonable_Effectiveness_of_Mathematics_in_the_Natural_Sciences Large Cardinal game based on 2048: http://cantorontheshore.blogspot.it/2014/10/one-reinhardt-and-counting.html Other good resources: http://quibb.blogspot.com/2012/01/infinity-first-transfinite-cardinal.html http://plato.stanford.edu/entries/set-theory/ http://cantorsattic.info/Cantor%27s_Attic http://cantorontheshore.blogspot.co.at/2014/09/artemis-fowl-and-large-cardinals_22.html http://isomorphism.es/post/10782081422/what-comes-after-infinity-transfinite-arithmetic-and-ord https://lukepalmer.wordpress.com/2007/06/14/the-lesser-of-infinitely-many-evils/ MUSIC BY: http://www.youtube.com/JakeChudnow http://www.audionetwork.com -
 8:00
8:00Infinity is bigger than you think - Numberphile
Infinity is bigger than you think - NumberphileInfinity is bigger than you think - Numberphile
Sometimes infinity is even bigger than you think... Dr James Grime explains with a little help from Georg Cantor. Website: http://www.numberphile.com/ Numberphile on Facebook: http://www.facebook.com/numberphile Numberphile tweets: https://twitter.com/numberphile James Grime: http://singingbanana.com/ Videos by Brady Haran Minute Physics video on this topic http://www.youtube.com/watch?v=A-QoutHCu4o (somewhat more fast-paced... but we did film ours BEFORE his was uploaded, so similarities are coincidental... well actually, no they are not... we are all building upon Cantor's work!!) -
 9:35
9:35Aleph number
Aleph numberAleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph. The cardinality of the natural numbers is , the next larger cardinality is aleph-one , then and so on. Continuing in this manner, it is possible to define a cardinal number for every ordinal number α, as described below. This video is targeted to blind users. Attribution: Article text available under CC-BY-SA Creative Commons image source in video -
 9:07
9:07Aleph number
Aleph numberAleph number
Aleph number In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality (or size) of infinite sets.They are named after the symbol used to denote them, the Hebrew letter aleph () (though in older mathematics books the letter aleph is often printed upside down by accident, partly because a Monotype matrix for aleph was mistakenly constructed the wrong way up ). -Video is targeted to blind users Attribution: Article text available under CC-BY-SA image source in video https://www.youtube.com/watch?v=_wFxi22PF9w -
 14:56
14:56How many kinds of infinity are there?
How many kinds of infinity are there? -
 1:19
1:19ALEPH NUMBER 1 THE OX
ALEPH NUMBER 1 THE OX -
 8:54
8:54Different Infinities-Series on Infinity Part 6
Different Infinities-Series on Infinity Part 6Different Infinities-Series on Infinity Part 6
This video presents Cantor's argument that there exist different infinities by demonstrating a set that is uncountable. It will only make sense if you have watched the previous video, Part 5, which defines countable sets. In essence, the size, or cardinality, of the rational numbers (fractions) is the smallest infinity: aleph null (or aleph zero). The cardinality of the real numbers, aleph one, is probably the next largest infinity, but that fact (the continuum hypothesis) has been shown to be impossible to prove under the current axioms of set theory. -
 6:24
6:24Aleph number or I dont know
Aleph number or I dont know -
 11:50
11:50Who are the ALEPH? | Infinity Week Discussion
Who are the ALEPH? | Infinity Week DiscussionWho are the ALEPH? | Infinity Week Discussion
The guys from Corvus Belli, creators of Infinity, give us the run down on one of the most mysterious factions in the Infinity game. The techno-organic ALEPH. -
 5:23
5:23Some Infinities are bigger than other Infinities
Some Infinities are bigger than other InfinitiesSome Infinities are bigger than other Infinities
Infinity is one of the most interesting concepts in mathematics, and while most people have some idea of what it is as a concept, many only know of an extremely simplified version of this idea - the simple concept of "the biggest number". With so many ideas at the forefront of science relying heavily on this supposedly useless number (the study of black holes and quantum mechanics being just a few), it seems a shame to reduce this incredibly important and complex topic down to just a single sentence. Concepts discussed: Aleph Null: https://en.wikipedia.org/wiki/Aleph_number Hilbert's Paradox of the Grand Hotel: https://en.wikipedia.org/wiki/Hilbert%27s_paradox_of_the_Grand_Hotel Uncountable sets: https://en.wikipedia.org/wiki/Uncountable_set Cantor's Diagonal Argument: https://en.wikipedia.org/wiki/Cantor%27s_diagonal_argument This video was produced for the Breakthrough Junior Challenge. For more information, please see: https://www.breakthroughjuniorchallenge.org
-

How To Count Past Infinity
Vote for Vsauce in the WEBBYS! https://pv.webbyawards.com/2016/online-film-video/video-channels-and-networks/science-education Sources and links to learn more below! I’m very grateful to mathematician Hugh Woodin, Professor of Philosophy and Mathematics at Harvard, for taking the time on multiple occasions to discuss this topic with me and help me wrap my (finite) head around it. I’m also grateful to David Eisenbud, the Director of the Mathematical Sciences Research Institute (MSRI) and professor of mathematics at the University of California, Berkeley, for his help and for connecting me with Hugh Woodin. And of course, big thanks to Brady Haran who created the “mile of pi” seen in this video and connected me with all these mathematicians in the first place. His channel, Numberphile, i...
published: 09 Apr 2016 -

Infinity is bigger than you think - Numberphile
Sometimes infinity is even bigger than you think... Dr James Grime explains with a little help from Georg Cantor. Website: http://www.numberphile.com/ Numberphile on Facebook: http://www.facebook.com/numberphile Numberphile tweets: https://twitter.com/numberphile James Grime: http://singingbanana.com/ Videos by Brady Haran Minute Physics video on this topic http://www.youtube.com/watch?v=A-QoutHCu4o (somewhat more fast-paced... but we did film ours BEFORE his was uploaded, so similarities are coincidental... well actually, no they are not... we are all building upon Cantor's work!!)
published: 06 Jul 2012 -

Aleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph. The cardinality of the natural numbers is , the next larger cardinality is aleph-one , then and so on. Continuing in this manner, it is possible to define a cardinal number for every ordinal number α, as described below. This video is targeted to blind users. Attribution: Article text available under CC-BY-SA Creative Commons image source in video
published: 30 Nov 2015 -

Aleph number
Aleph number In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality (or size) of infinite sets.They are named after the symbol used to denote them, the Hebrew letter aleph () (though in older mathematics books the letter aleph is often printed upside down by accident, partly because a Monotype matrix for aleph was mistakenly constructed the wrong way up ). -Video is targeted to blind users Attribution: Article text available under CC-BY-SA image source in video https://www.youtube.com/watch?v=_wFxi22PF9w
published: 22 Jan 2016 -

-

-

Different Infinities-Series on Infinity Part 6
This video presents Cantor's argument that there exist different infinities by demonstrating a set that is uncountable. It will only make sense if you have watched the previous video, Part 5, which defines countable sets. In essence, the size, or cardinality, of the rational numbers (fractions) is the smallest infinity: aleph null (or aleph zero). The cardinality of the real numbers, aleph one, is probably the next largest infinity, but that fact (the continuum hypothesis) has been shown to be impossible to prove under the current axioms of set theory.
published: 14 Sep 2008 -

-

Who are the ALEPH? | Infinity Week Discussion
The guys from Corvus Belli, creators of Infinity, give us the run down on one of the most mysterious factions in the Infinity game. The techno-organic ALEPH.
published: 13 Dec 2011 -

Some Infinities are bigger than other Infinities
Infinity is one of the most interesting concepts in mathematics, and while most people have some idea of what it is as a concept, many only know of an extremely simplified version of this idea - the simple concept of "the biggest number". With so many ideas at the forefront of science relying heavily on this supposedly useless number (the study of black holes and quantum mechanics being just a few), it seems a shame to reduce this incredibly important and complex topic down to just a single sentence. Concepts discussed: Aleph Null: https://en.wikipedia.org/wiki/Aleph_number Hilbert's Paradox of the Grand Hotel: https://en.wikipedia.org/wiki/Hilbert%27s_paradox_of_the_Grand_Hotel Uncountable sets: https://en.wikipedia.org/wiki/Uncountable_set Cantor's Diagonal Argument: https://en.wikipedi...
published: 04 Oct 2015
How To Count Past Infinity
- Order: Reorder
- Duration: 23:46
- Updated: 09 Apr 2016
- views: 7076863
- published: 09 Apr 2016
- views: 7076863
Infinity is bigger than you think - Numberphile
- Order: Reorder
- Duration: 8:00
- Updated: 06 Jul 2012
- views: 4743541
- published: 06 Jul 2012
- views: 4743541
Aleph number
- Order: Reorder
- Duration: 9:35
- Updated: 30 Nov 2015
- views: 437
- published: 30 Nov 2015
- views: 437
Aleph number
- Order: Reorder
- Duration: 9:07
- Updated: 22 Jan 2016
- views: 43
- published: 22 Jan 2016
- views: 43
How many kinds of infinity are there?
- Order: Reorder
- Duration: 14:56
- Updated: 06 Jun 2014
- views: 387169
ALEPH NUMBER 1 THE OX
- Order: Reorder
- Duration: 1:19
- Updated: 13 Jan 2017
- views: 73
Different Infinities-Series on Infinity Part 6
- Order: Reorder
- Duration: 8:54
- Updated: 14 Sep 2008
- views: 12360
- published: 14 Sep 2008
- views: 12360
Aleph number or I dont know
- Order: Reorder
- Duration: 6:24
- Updated: 04 Jun 2016
- views: 159
Who are the ALEPH? | Infinity Week Discussion
- Order: Reorder
- Duration: 11:50
- Updated: 13 Dec 2011
- views: 6415
- published: 13 Dec 2011
- views: 6415
Some Infinities are bigger than other Infinities
- Order: Reorder
- Duration: 5:23
- Updated: 04 Oct 2015
- views: 1352
- published: 04 Oct 2015
- views: 1352
- Playlist
- Chat
- Playlist
- Chat

How To Count Past Infinity
- Report rights infringement
- published: 09 Apr 2016
- views: 7076863

Infinity is bigger than you think - Numberphile
- Report rights infringement
- published: 06 Jul 2012
- views: 4743541

Aleph number
- Report rights infringement
- published: 30 Nov 2015
- views: 437

Aleph number
- Report rights infringement
- published: 22 Jan 2016
- views: 43

How many kinds of infinity are there?
- Report rights infringement
- published: 06 Jun 2014
- views: 387169

ALEPH NUMBER 1 THE OX
- Report rights infringement
- published: 13 Jan 2017
- views: 73

Different Infinities-Series on Infinity Part 6
- Report rights infringement
- published: 14 Sep 2008
- views: 12360

Aleph number or I dont know
- Report rights infringement
- published: 04 Jun 2016
- views: 159

Who are the ALEPH? | Infinity Week Discussion
- Report rights infringement
- published: 13 Dec 2011
- views: 6415

Some Infinities are bigger than other Infinities
- Report rights infringement
- published: 04 Oct 2015
- views: 1352
Donald Trump inauguration live: Billionaire reality TV star to become US President amid massive protests
Edit The Independent 20 Jan 2017Was Fort Lauderdale Shooter Another Case of Deep State’s MKUltra-Mind Control?
Edit WorldNews.com 20 Jan 2017Spain Arrests Russian Programmer Over Hacking On US Request
Edit WorldNews.com 20 Jan 2017Osama Bin Laden Documents: Worry Over ISIS Tactics, 'Aging' Al-Qaeda
Edit NDTV 20 Jan 2017BREAKING: Report Say Eight Survivors Found Inside Italian Hotel Buried By Avalanche
Edit WorldNews.com 20 Jan 2017Natalie Portman: ‘JFK was a great proponent of civil rights. Trump is taking us backwards’
Edit The Guardian 19 Jan 2017Much hype, few sales
Edit DNA India 15 Jan 2017Interview: Natalie Portman on making her new film, Jackie
Edit Scotsman 14 Jan 2017Case of 'fattened' Jorge Luis Borges story headed to court in Argentina
Edit The Guardian 10 Jan 2017Natalie Portman: bringing Jackie Onassis back to life
Edit The Guardian 08 Jan 201710 books we’re watching out for this year
Edit Hindustan Times 07 Jan 2017An anthology that takes you into the dark places of the mind
Edit Hindustan Times 06 Jan 2017What to read in 2017
Edit Kashmir Observer 02 Jan 2017Interview with a bookstore: DIESEL, A Bookstore in California
Edit The Guardian 02 Jan 2017Distrust Forecasts
Edit Seeking Alpha 01 Jan 2017A collection of short stories that promises to linger on for a long time
Edit Hindustan Times 30 Dec 2016The Best Reads of 2016
Edit Hindustan Times 30 Dec 2016The Best Writing Advice of 2016
Edit The Atlantic 27 Dec 2016- 1
- 2
- 3
- 4
- 5
- Next page »








