- published: 05 Feb 2013
- views: 171542
-
remove the playlistCircular Motion
- remove the playlistCircular Motion
- published: 28 Oct 2013
- views: 31446
- published: 13 Sep 2009
- views: 177686
- published: 18 Jan 2016
- views: 1055
- published: 22 Nov 2011
- views: 261957
- published: 26 Sep 2012
- views: 44202
- published: 20 Jul 2012
- views: 47632
- published: 10 Dec 2014
- views: 36564
- published: 21 Dec 2007
- views: 83185
- published: 22 Apr 2012
- views: 73178
- published: 26 May 2014
- views: 14535

In physics, circular motion is a movement of an object along the circumference of a circle or rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation (and thus constant speed), or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of its parts. The equations describing circular motion of an object do not take size or geometry into account, rather, the motion of a point mass in a plane is assumed. In practice, the center of mass of a body can be considered to undergo circular motion.
Examples of circular motion include: an artificial satellite orbiting the Earth at constant height, a stone which is tied to a rope and is being swung in circles, a car turning through a curve in a race track, an electron moving perpendicular to a uniform magnetic field, and a gear turning inside a mechanism.
Circular motion is accelerated even if the angular rate of rotation is constant, because the object's velocity vector is constantly changing direction. Such change in direction of velocity involves acceleration of the moving object by a centripetal force, which pulls the moving object toward the center of the circular orbit. Without this acceleration, the object would move in a straight line, according to Newton's laws of motion.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...

-
 27:29
27:29Circular Motion - A Level Physics
Circular Motion - A Level PhysicsCircular Motion - A Level Physics
Consideration of Circular Motion, orbital speed, angular speed, centripetal acceleration and force - with some worked example. -
 9:11
9:11Intro to Circular Motion! (a tribute to Lou Reed) | Doc Physics
Intro to Circular Motion! (a tribute to Lou Reed) | Doc PhysicsIntro to Circular Motion! (a tribute to Lou Reed) | Doc Physics
A strange condition must be met for things to go in a circle. I'm not sure you've realized just how lucky you are, Ducky. -
 9:23
9:23Circular Motion Problems
Circular Motion ProblemsCircular Motion Problems
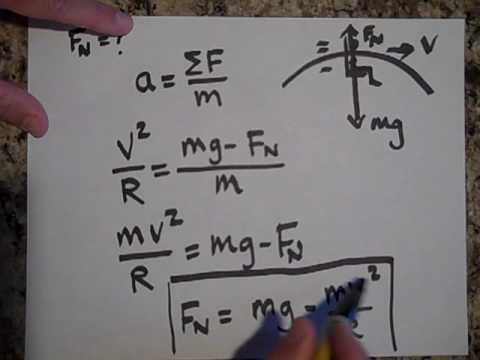
Illustrates how to use Newton's second law to solve circular motion problems. For a complete index of these videos visit http://www.apphysicslectures.com -
 4:35
4:35Circular Motion | A-Level Physics | Doodle Science
Circular Motion | A-Level Physics | Doodle ScienceCircular Motion | A-Level Physics | Doodle Science
A Level Physics Doodle Science teaches you high school and College physics in a less boring way in almost no time! Follow me: https://twitter.com/DoodleSci You can support me at: https://patreon.com/doodlescience Script: Circular motion is simply the physics of things moving in circles. This happens all the time, for example you are moving in a circle around the earth as it rotates about its axis. If you are on the equator you would be moving through a larger circle per day than if you were in London, which is much further north. However, both of these places would have the same angular displacement at any point in the day. The angular displacement is measured in radians rather than degrees because it makes calculations much more straightforward. For example, the distance you move along the circle is given by the formula s = r θ. Where s is the arc length in metres, r is the radius of the circle in metres and θ is the angular displacement in radians. There are 2π radians in a circle, which means that 2π = 360 degrees and using this fact we can convert between degrees and radians. For example, an aeroplane performing a loop de loop of radius 60m turns through 135 degrees. To calculate the distance the plane has moved we have to first convert the degrees into radians. This is done by dividing 2π/360 to get the radians for 1 degree and multiplying it by 135, which gives ¾ π or 2.36 radians. This can then be used to work out the distance the plane has travelled as being 141m. When an object undergoes circular motion, the object will move at a constant speed but changing velocity. The velocity is changing because the direction is constantly changing and velocity is both speed and direction. This means that there is an acceleration, called the centripetal acceleration. The formula for this is a = v^2/r, where v is the velocity and r is the radius. Another relationship in circular motion is ω = v/r, where ω is the angular speed, which is a measrure of how many radians are being turned through per second and it is measured in rad/s. Another formula for ω is 2π/T where T is the time period of one complete rotation measured in seconds. A centripetal force must be occuring here in order to produce this acceleration. The formula for centripetal force is F = mv^2/r. Where m is the mass of the body undergoing circular motion, v is the velocity and r is the radius of the circle. For example, another aircraft display team perform a horizontal circle of radius 350m travelling at 100m/s. From this we can work out the angular speed as being 0.286 rad/s. If the mass of the pilot was 75kg, then we could work out the centripetal force as being 2140N. It’s important to determine which forces are directed towards and away from the centre of the circle in order to determine the resultant force which is equal to the centripetal force. For example going back to the loop de loop performed by the aircraft, there are 2 points in the stunt that are of interest, at the top and at the bottom of the circle. At the top, the normal reaction force of the pilot from his seat and his weight are both acting downwards, towards the centre of the circle. At the bottom of the circle, the normal reaction force acts up towards the centre of the circle and the weight acts down. Given that the pilot had a mass of 80kg and the plane was travelling at 100m/s we can work out the normal reaction force on the pilot at the bottom of the circle to be 14100N and at the top the normal reaction force as 12500N which is a very strong force. References: 1. CGP AS & A2 Physics for OCR A, ISBN: 9781847624192 -
 10:47
10:47Centripetal Force and Acceleration Intuition
Centripetal Force and Acceleration IntuitionCentripetal Force and Acceleration Intuition
The direction of the force in cases of circular motion at constant speeds More free lessons at: http://www.khanacademy.org/video?v=vZOk8NnjILg -
 7:32
7:32Hewitt-Drew-it! PHYSICS 35. Circular Motion
Hewitt-Drew-it! PHYSICS 35. Circular MotionHewitt-Drew-it! PHYSICS 35. Circular Motion
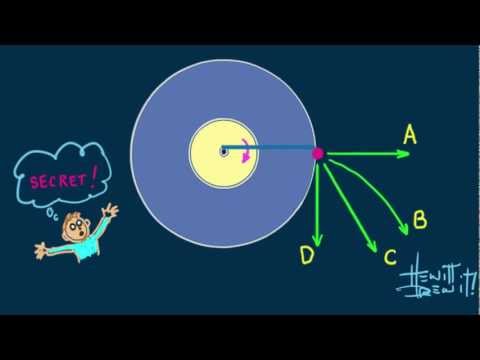
Paul discusses his father working as a ticket collector in a merry-go-round and ties this to a Burl-Grey problem involving circular motion. -
 67:26
67:26XI 34 Circular Motion basics
XI 34 Circular Motion basicsXI 34 Circular Motion basics
Class XI Physics Class room Lecture by Pradeep Kshetrapal. Chapter : Two dimension motion. Topic : Circular motion Basics. Language Hindi and English mixed. -
 50:51
50:51Lec 05: Uniform Circular Motion | 8.01 Classical Mechanics, Fall 1999 (Walter Lewin)
Lec 05: Uniform Circular Motion | 8.01 Classical Mechanics, Fall 1999 (Walter Lewin)Lec 05: Uniform Circular Motion | 8.01 Classical Mechanics, Fall 1999 (Walter Lewin)
This lecture is about uniform circular motion. There is a constant radial acceleration (centripetal acceleration) but constant tangential speed. This lecture is part of 8.01 Physics I: Classical Mechanics, as taught in Fall 1999 by Dr. Walter Lewin at MIT. This video was formerly hosted on the YouTube channel MIT OpenCourseWare. This version was downloaded from the Internet Archive, at https://archive.org/details/MIT8.01F99/. Attribution: MIT OpenCourseWare License: Creative Commons BY-NC-SA 3.0 US To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/us/. More information at http://ocw.mit.edu/terms/. This YouTube channel is independently operated. It is not affiliated with MIT, MIT OpenCourseWare, the Internet Archive, or Dr. Lewin, nor do they endorse any content on this channel. -
 5:17
5:17Circular Motion
Circular MotionCircular Motion
A physics video project that explains the concept of circular motion, including centripetal acceleration, centripetal force, and other equations. Examples include roller coaster, hammer throw, race car, moon orbit. Wide screen (16:9) Won 4 out of 5 "Acade-marr Awards" in 2007 at Hugh McRoberts Secondary, including Best Picture Best Directing/Editing Best Special Effects Best Sound Effects -
 5:25
5:25Physics - Mechanics: Motion In Two-Dimension: (16 of 21) Circular Motion and Acceleration
Physics - Mechanics: Motion In Two-Dimension: (16 of 21) Circular Motion and Acceleration -
 4:21
4:21Physics Lecture - 16 - Circular Motion / Centripetal Force
Physics Lecture - 16 - Circular Motion / Centripetal ForcePhysics Lecture - 16 - Circular Motion / Centripetal Force
Visit my website at https://www.thenewboston.com/ for all of my videos and tutorials! Have questions or looking for source code? Check out the forum at https://www.thenewboston.com/forum/ My Profile - https://www.thenewboston.com/profile.php?user=2 Facebook - http://www.facebook.com/pages/TheNewBoston/464114846956315 Google+ - https://plus.google.com/+BuckyRoberts/posts Twitter - http://twitter.com/#!/bucky_roberts Donate - https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted;_button_id=5K9RJVCAKWZKS -
 63:06
63:06IIT JEE Main + Advanced | Physics | Circular motion | NM Sir from etoosindia.com
IIT JEE Main + Advanced | Physics | Circular motion | NM Sir from etoosindia.comIIT JEE Main + Advanced | Physics | Circular motion | NM Sir from etoosindia.com
"Circular Motion video Lecture of Physics for IIT-JEE Main and Advanced by NM Sir. NM Sir is known for his focused and simplified JEE teaching to bring to students an easy and analytical methodology towards IIT-JEE. This course is designed and developed by the experienced faculty of KOTA and www.etoosindia.com. #phy nm circular motion p-nm-12-0103-circular-motion-140501-vh "
- Alexis Clairaut
- Analytical dynamics
- Analytical mechanics
- Angular acceleration
- Angular displacement
- Angular frequency
- Angular momentum
- Angular velocity
- Applied mechanics
- Celestial mechanics
- Center of mass
- Centrifugal force
- Centripetal force
- Circle
- Circular motion
- Circumference
- Complex number
- Continuum mechanics
- Coriolis effect
- Couple (mechanics)
- Cross product
- Damping
- Damping ratio
- Energy
- Equations of motion
- Fictitious force
- Force
- Frame of reference
- Frequency
- Friction
- Galileo Galilei
- Gear
- Gravitation
- Harmonic oscillator
- Hertz
- Imaginary unit
- Impulse (physics)
- Inertia
- Isaac Newton
- Jeremiah Horrocks
- Joule
- Kinematics
- Kinetic energy
- Kinetics (physics)
- Lagrangian mechanics
- Leonhard Euler
- Linear motion
- Magnetic field
- Mass
- Moment (physics)
- Moment of inertia
- Momentum
- Motion (physics)
- Newton (unit)
- Nu (letter)
- Omega
- Orbit
- Orthogonality
- Physics
- Pi
- Pierre-Simon Laplace
- Planck's constant
- Potential energy
- Quantum mechanics
- Race track
- Radian
- Radius
- Reciprocating motion
- Relative velocity
- Right-hand rule
- Rigid body
- Rigid body dynamics
- Rotation
- Rotational speed
- Second
- Siméon Denis Poisson
- Space
- Speed
- Statics
- Talk Circular motion
- Time
- Time derivative
- Torque
- Turn (geometry)
- Unit vector
- Vector (geometry)
- Velocity
- Vibration
- Virtual work
- Wikipedia Merging
- Work (physics)
-

Circular Motion - A Level Physics
Consideration of Circular Motion, orbital speed, angular speed, centripetal acceleration and force - with some worked example. -

Intro to Circular Motion! (a tribute to Lou Reed) | Doc Physics
A strange condition must be met for things to go in a circle. I'm not sure you've realized just how lucky you are, Ducky. -

Circular Motion Problems
Illustrates how to use Newton's second law to solve circular motion problems. For a complete index of these videos visit http://www.apphysicslectures.com -

Circular Motion | A-Level Physics | Doodle Science
A Level Physics Doodle Science teaches you high school and College physics in a less boring way in almost no time! Follow me: https://twitter.com/DoodleSci You can support me at: https://patreon.com/doodlescience Script: Circular motion is simply the physics of things moving in circles. This happens all the time, for example you are moving in a circle around the earth as it rotates about its axis. If you are on the equator you would be moving through a larger circle per day than if you were in London, which is much further north. However, both of these places would have the same angular displacement at any point in the day. The angular displacement is measured in radians rather than degrees because it makes calculations much more straightforward. For example, the distance you move alon... -

Centripetal Force and Acceleration Intuition
The direction of the force in cases of circular motion at constant speeds More free lessons at: http://www.khanacademy.org/video?v=vZOk8NnjILg -

Hewitt-Drew-it! PHYSICS 35. Circular Motion
Paul discusses his father working as a ticket collector in a merry-go-round and ties this to a Burl-Grey problem involving circular motion. -

XI 34 Circular Motion basics
Class XI Physics Class room Lecture by Pradeep Kshetrapal. Chapter : Two dimension motion. Topic : Circular motion Basics. Language Hindi and English mixed. -

Lec 05: Uniform Circular Motion | 8.01 Classical Mechanics, Fall 1999 (Walter Lewin)
This lecture is about uniform circular motion. There is a constant radial acceleration (centripetal acceleration) but constant tangential speed. This lecture is part of 8.01 Physics I: Classical Mechanics, as taught in Fall 1999 by Dr. Walter Lewin at MIT. This video was formerly hosted on the YouTube channel MIT OpenCourseWare. This version was downloaded from the Internet Archive, at https://archive.org/details/MIT8.01F99/. Attribution: MIT OpenCourseWare License: Creative Commons BY-NC-SA 3.0 US To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/us/. More information at http://ocw.mit.edu/terms/. This YouTube channel is independently operated. It is not affiliated with MIT, MIT OpenCourseWare, the Internet Archive, or Dr. Lewin, nor do they endors... -

Circular Motion
A physics video project that explains the concept of circular motion, including centripetal acceleration, centripetal force, and other equations. Examples include roller coaster, hammer throw, race car, moon orbit. Wide screen (16:9) Won 4 out of 5 "Acade-marr Awards" in 2007 at Hugh McRoberts Secondary, including Best Picture Best Directing/Editing Best Special Effects Best Sound Effects -

-

Physics Lecture - 16 - Circular Motion / Centripetal Force
Visit my website at https://www.thenewboston.com/ for all of my videos and tutorials! Have questions or looking for source code? Check out the forum at https://www.thenewboston.com/forum/ My Profile - https://www.thenewboston.com/profile.php?user=2 Facebook - http://www.facebook.com/pages/TheNewBoston/464114846956315 Google+ - https://plus.google.com/+BuckyRoberts/posts Twitter - http://twitter.com/#!/bucky_roberts Donate - https://www.paypal.com/cgi-bin/webscr?cmd=_s-xclick&hosted;_button_id=5K9RJVCAKWZKS -

IIT JEE Main + Advanced | Physics | Circular motion | NM Sir from etoosindia.com
"Circular Motion video Lecture of Physics for IIT-JEE Main and Advanced by NM Sir. NM Sir is known for his focused and simplified JEE teaching to bring to students an easy and analytical methodology towards IIT-JEE. This course is designed and developed by the experienced faculty of KOTA and www.etoosindia.com. #phy nm circular motion p-nm-12-0103-circular-motion-140501-vh "
Circular Motion - A Level Physics
- Order: Reorder
- Duration: 27:29
- Updated: 05 Feb 2013
- views: 171542
- published: 05 Feb 2013
- views: 171542
Intro to Circular Motion! (a tribute to Lou Reed) | Doc Physics
- Order: Reorder
- Duration: 9:11
- Updated: 28 Oct 2013
- views: 31446
- published: 28 Oct 2013
- views: 31446
Circular Motion Problems
- Order: Reorder
- Duration: 9:23
- Updated: 13 Sep 2009
- views: 177686
- published: 13 Sep 2009
- views: 177686
Circular Motion | A-Level Physics | Doodle Science
- Order: Reorder
- Duration: 4:35
- Updated: 18 Jan 2016
- views: 1055
- published: 18 Jan 2016
- views: 1055
Centripetal Force and Acceleration Intuition
- Order: Reorder
- Duration: 10:47
- Updated: 22 Nov 2011
- views: 261957
- published: 22 Nov 2011
- views: 261957
Hewitt-Drew-it! PHYSICS 35. Circular Motion
- Order: Reorder
- Duration: 7:32
- Updated: 26 Sep 2012
- views: 44202
- published: 26 Sep 2012
- views: 44202
XI 34 Circular Motion basics
- Order: Reorder
- Duration: 67:26
- Updated: 20 Jul 2012
- views: 47632
- published: 20 Jul 2012
- views: 47632
Lec 05: Uniform Circular Motion | 8.01 Classical Mechanics, Fall 1999 (Walter Lewin)
- Order: Reorder
- Duration: 50:51
- Updated: 10 Dec 2014
- views: 36564
- published: 10 Dec 2014
- views: 36564
Circular Motion
- Order: Reorder
- Duration: 5:17
- Updated: 21 Dec 2007
- views: 83185
- published: 21 Dec 2007
- views: 83185
Physics - Mechanics: Motion In Two-Dimension: (16 of 21) Circular Motion and Acceleration
- Order: Reorder
- Duration: 5:25
- Updated: 21 Aug 2013
- views: 27888
Physics Lecture - 16 - Circular Motion / Centripetal Force
- Order: Reorder
- Duration: 4:21
- Updated: 22 Apr 2012
- views: 73178
- published: 22 Apr 2012
- views: 73178
IIT JEE Main + Advanced | Physics | Circular motion | NM Sir from etoosindia.com
- Order: Reorder
- Duration: 63:06
- Updated: 26 May 2014
- views: 14535
- published: 26 May 2014
- views: 14535
- Playlist
- Chat
- Playlist
- Chat

Circular Motion - A Level Physics
- Report rights infringement
- published: 05 Feb 2013
- views: 171542

Intro to Circular Motion! (a tribute to Lou Reed) | Doc Physics
- Report rights infringement
- published: 28 Oct 2013
- views: 31446

Circular Motion Problems
- Report rights infringement
- published: 13 Sep 2009
- views: 177686

Circular Motion | A-Level Physics | Doodle Science
- Report rights infringement
- published: 18 Jan 2016
- views: 1055

Centripetal Force and Acceleration Intuition
- Report rights infringement
- published: 22 Nov 2011
- views: 261957

Hewitt-Drew-it! PHYSICS 35. Circular Motion
- Report rights infringement
- published: 26 Sep 2012
- views: 44202

XI 34 Circular Motion basics
- Report rights infringement
- published: 20 Jul 2012
- views: 47632

Lec 05: Uniform Circular Motion | 8.01 Classical Mechanics, Fall 1999 (Walter Lewin)
- Report rights infringement
- published: 10 Dec 2014
- views: 36564

Circular Motion
- Report rights infringement
- published: 21 Dec 2007
- views: 83185

Physics - Mechanics: Motion In Two-Dimension: (16 of 21) Circular Motion and Acceleration
- Report rights infringement
- published: 21 Aug 2013
- views: 27888

Physics Lecture - 16 - Circular Motion / Centripetal Force
- Report rights infringement
- published: 22 Apr 2012
- views: 73178

IIT JEE Main + Advanced | Physics | Circular motion | NM Sir from etoosindia.com
- Report rights infringement
- published: 26 May 2014
- views: 14535
RNC Chairman Says Trump "Trying" To Rein In Craziness Surrounding His Campaign
Edit WorldNews.com 06 May 2016US magazine names British star in media gag over 'sex with prostitute'
Edit Belfast Telegraph 05 May 2016Oil tanker washes up on Liberia beach with no crew or lifeboats
Edit The Guardian 06 May 2016After a Landmark Legal Ruling, Will CIA Torture Victims Finally Have Their Day in Court?
Edit Democracy Now 06 May 20169 things you should know if your child is using heroin
Edit Raw Story 06 May 2016IVF: 'I had the dread feeling that I was part of some greater experiment'
Edit The Guardian 06 May 2016Why men should exfoliate and how to do it?
Edit The Examiner 04 May 2016Burglary, theft, among indictments in Hunterdon County
Edit NJ dot com 03 May 2016The Bar Amigos ® Turbulence Bohemian Crystal Wine Glass Range is really brewing up a storm!
Edit Pressat 03 May 2016Hindu children honor their teachers in program at New Cumberland temple
Edit Penn Live 02 May 2016MY GUMS ARE GROWING OVER MY BRACES. WHY?
Edit The Examiner 02 May 2016Tone your upper body this summer
Edit The Examiner 30 Apr 2016Co-owner of Precious Paws Pet Spa in Dubai makes sure every guest is pampered
Edit The National 30 Apr 20165 must try low calorie dishes
Edit The Times of India 29 Apr 2016What does Brazil's political crisis mean for the 2016 Rio Olympic Games?
Edit Sydney Morning Herald 29 Apr 2016Braving temps of -47, New York Airmen build snow runway in High Arctic (The National Guard)
Edit Public Technologies 26 Apr 2016In Rome, 'everything is beautiful'
Edit Stuff 26 Apr 2016Review: Golden Door Bamboo Scrub
Edit The Examiner 20 Apr 2016- 1
- 2
- 3
- 4
- 5
- Next page »







