Branches of Mathematics
Pure mathematics
Applied mathematics
- Dynamical systems and differential equations
- Mathematical physics
- Computing
- Information theory and signal processing
- Probability and statistics
- Game theory
- Operations research
Related Topics
- Electromagnetic Spectrum
- Linear Equations
- Applied Physics
- Nano Technology
- Engineering Sciences
- Mathematical Medicine
- Fluid dynamics
- Computational Mathematics
- Gamma Ray Optics
- Onfrared Optics
- Relative Velocity
- Iciam
- Intelligent Imaging Neuroscience
- Biomedical Engineering
- Neuroscience Research
- Quantum Cosmology
- Brain Research

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size (enumerative combinatorics), deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria (as in combinatorial designs and matroid theory), finding "largest", "smallest", or "optimal" objects (extremal combinatorics and combinatorial optimization), and studying combinatorial structures arising in an algebraic context, or applying algebraic techniques to combinatorial problems (algebraic combinatorics).
Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry, and combinatorics also has many applications in optimization, computer science, ergodic theory and statistical physics. Many combinatorial questions have historically been considered in isolation, giving an ad hoc solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics is graph theory, which also has numerous natural connections to other areas. Combinatorics is used frequently in computer science to obtain formulas and estimates in the analysis of algorithms.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...

-
Basic Combinatorics- Part 1
Basic Combinatorics- Part 1 -
Getting Exactly Two Heads (Combinatorics)
Getting Exactly Two Heads (Combinatorics)Getting Exactly Two Heads (Combinatorics)
Learn more: http://www.khanacademy.org/video?v=8TIben0bJpU A different way to think about the probability of getting 2 heads in 4 flips. -
MathHistory29: Combinatorics
MathHistory29: CombinatoricsMathHistory29: Combinatorics
We give a brief historical introduction to the vibrant modern theory of combinatorics, concentrating on examples coming from counting problems, graph theory and generating functions. In particular we look at partitions and Euler's pentagonal theorem, Fibonacci numbers, the Catalan sequence, the Erdos Szekeres theorem, Ramsey theory and the Kirkman Schoolgirls problem. -
Introduction to Combinatorics : Principles of Math
Introduction to Combinatorics : Principles of MathIntroduction to Combinatorics : Principles of Math
Subscribe Now: http://www.youtube.com/subscription_center?add_user=Ehow Watch More: http://www.youtube.com/Ehow Combinatorics is a very important course in t... -
Combinatorics with Day[9]: Bijections
Combinatorics with Day[9]: BijectionsCombinatorics with Day[9]: Bijections
Combinatorics with Day[9]: Bijections. -
Lecture 1 . Enumerative Combinatorics (Federico Ardila)
Lecture 1 . Enumerative Combinatorics (Federico Ardila)Lecture 1 . Enumerative Combinatorics (Federico Ardila)
Much of enumerative combinatorics concerns the question: "Count the number a_n of elements of a set S_n for n=1,2,..." We discuss four types of answers: an e... -
Algebra II: binomial Expansion and Combinatorics
Algebra II: binomial Expansion and CombinatoricsAlgebra II: binomial Expansion and Combinatorics
65 (done another way) - 66, combinatorics and binomial expansions -
Extremal and Probabilistic Combinatorics Aula 1 Parte 1
Extremal and Probabilistic Combinatorics Aula 1 Parte 1Extremal and Probabilistic Combinatorics Aula 1 Parte 1
Extremal and Probabilistic Combinatorics In this course we will introduce the student to the basic theorems and proof techniques in extremal graph theory and probabilistic combinatorics. We shall emphasize the close links between these two areas, and provide the background material for modern research fields such as additive combinatorics, monotone and hereditary properties, and graph limits. We also discuss some simple but powerful applications of techniques from functional analysis and linear algebra. The course has no prerequisites. Programa: 1. Ramsey Theory: Finite and infinite versions. Erdös' random proof of the lower bound. Van de -
Counting and Combinatorics in Discrete Math Part 1
Counting and Combinatorics in Discrete Math Part 1Counting and Combinatorics in Discrete Math Part 1
This is part 1 of learning basic counting and combinations in discrete mathematics. I will give some examples to get you introduced to the idea of finding combinations. -
GMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT Prep
GMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT PrepGMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT Prep
http://www.manhattanreview.com/gmat-online/. This video covers the permutation and combinatorics problems in the GMAT Math Problem Solving section. Manhattan... -
How To Do Combinatorics In Poker
How To Do Combinatorics In PokerHow To Do Combinatorics In Poker
http://nitreg.com How do you figure out combinatorics in poker? Watch this video and find out. The math is fairly easy and I show you a couple of examples to... -
Unizor - Combinatorics - Permutations
Unizor - Combinatorics - PermutationsUnizor - Combinatorics - Permutations
Combinatorics is a much newer part of mathematics than such classical subjects as Geometry or Algebra. Very important stimulus to its development was the Theory of Probabilities, which is the next subject in this course. Later on, Game Theory and contemporary Computer Science were the other fields of application of the combinatorics. The subject of Permutations is calculating the number of possibilities of putting certain number of objects in certain order. Examples are numerous. For instance, you have to visit 3 different places A, B and C. The order in which you visit them can be ABC, ACB, BAC, BCA, CAB and CBA. Actually, these 6 differen -
Alexander Postnikov (MIT) The Combinatorics of the Grassmanian I
Alexander Postnikov (MIT) The Combinatorics of the Grassmanian IAlexander Postnikov (MIT) The Combinatorics of the Grassmanian I
Alexander Postnikov (MIT) The Combinatorics of the Grassmanian I -
Combination formula
Combination formulaCombination formula
- Abstract algebra
- Algebra
- Algebraic geometry
- Algebraic topology
- Analysis
- Ancient history
- Ancient Rome
- Applied mathematics
- Archimedes
- Areas of mathematics
- Arithmetic
- Associahedron
- Astronomer
- Asymptotic analysis
- Automata theory
- Bijective proof
- Binary tree
- Binomial coefficient
- Birkhoff polytope
- Blaise Pascal
- Block design
- Boolean algebras
- Calculus
- Campanology
- Catalan number
- Category theory
- Cayley graph
- Change ringing
- Chromatic polynomial
- Chrysippus
- Coding theory
- Combinations
- Combinatorial design
- Combinatoriality
- Combinatorics
- Complex analysis
- Computer science
- Control theory
- Convex geometry
- Convex polytope
- Countable set
- Decision tree
- Discrete geometry
- Discrete mathematics
- Dynamical system
- Elementary algebra
- Ergodic theory
- Euclidean plane
- Fair division
- Fibonacci numbers
- Finite geometry
- Formal grammar
- Formal language
- Four color problem
- Fractal analysis
- Game theory
- Generating functions
- Geometry
- Gian-Carlo Rota
- Graph coloring
- Graph theory
- Group theory
- Hamiltonian cycle
- Harmonic analysis
- Hasse diagram
- Hassler Whitney
- Hipparchus
- Historian
- Icosahedron
- Inclusion map
- India
- Information theory
- Integer partition
- Isaac Newton
- Ising model
- Jacob Bernoulli
- Kissing number
- Lattice (order)
- Lattice graph
- Leonard Euler
- Levi ben Gerson
- Lie theory
- Linear algebra
- Linear independence
- Linguistics
- Markov chains
- Mathematical logic
- Mathematical physics
- Mathematical problem
- Mathematician
- Mathematics
- MathWorld
- Matroid
- Matroid theory
- Measure theory
- Medieval England
- Metric geometry
- Middle Ages
- Multilinear algebra
- Necklace problem
- Number theory
- Numerical analysis
- Operations research
- Order theory
- Ostomachion
- Partition of a set
- Pascal's triangle
- Paul Erdős
- Permutations
- Permutohedron
- Petersen graph
- Philosopher
- Phylogenetics
- Physician
- Pigeonhole principle
- Plane partition
- Plutarch
- Portal Mathematics
- Potts model
- Power set
- Probabilistic method
- Probability
- Probability theory
- Pure mathematics
- Q-series
- Ramsey theory
- Random graph
- Renaissance
- Richard P. Stanley
- Schröder number
- Science
- Self-avoiding walk
- Set intersection
- Set system
- Set theory
- Special functions
- Statistical physics
- Steiner system
- Sufficiently large
- Sushruta
- Sushruta Samhita
- Talmudist
- Thue-Morse sequence
- Tiling puzzle
- Topology
- Tutte polynomial
- Twelvefold way
- Vector space
- Young diagram
-
Basic Combinatorics- Part 1
Basic Combinatorics- Part 1Basic Combinatorics- Part 1
Introduction to combinations and permutations -
Getting Exactly Two Heads (Combinatorics)
Getting Exactly Two Heads (Combinatorics)Getting Exactly Two Heads (Combinatorics)
Learn more: http://www.khanacademy.org/video?v=8TIben0bJpU A different way to think about the probability of getting 2 heads in 4 flips. -
MathHistory29: Combinatorics
MathHistory29: CombinatoricsMathHistory29: Combinatorics
We give a brief historical introduction to the vibrant modern theory of combinatorics, concentrating on examples coming from counting problems, graph theory and generating functions. In particular we look at partitions and Euler's pentagonal theorem, Fibonacci numbers, the Catalan sequence, the Erdos Szekeres theorem, Ramsey theory and the Kirkman Schoolgirls problem. -
Introduction to Combinatorics : Principles of Math
Introduction to Combinatorics : Principles of MathIntroduction to Combinatorics : Principles of Math
Subscribe Now: http://www.youtube.com/subscription_center?add_user=Ehow Watch More: http://www.youtube.com/Ehow Combinatorics is a very important course in t... -
Combinatorics with Day[9]: Bijections
Combinatorics with Day[9]: BijectionsCombinatorics with Day[9]: Bijections
Combinatorics with Day[9]: Bijections. -
Lecture 1 . Enumerative Combinatorics (Federico Ardila)
Lecture 1 . Enumerative Combinatorics (Federico Ardila)Lecture 1 . Enumerative Combinatorics (Federico Ardila)
Much of enumerative combinatorics concerns the question: "Count the number a_n of elements of a set S_n for n=1,2,..." We discuss four types of answers: an e... -
Algebra II: binomial Expansion and Combinatorics
Algebra II: binomial Expansion and CombinatoricsAlgebra II: binomial Expansion and Combinatorics
65 (done another way) - 66, combinatorics and binomial expansions -
Extremal and Probabilistic Combinatorics Aula 1 Parte 1
Extremal and Probabilistic Combinatorics Aula 1 Parte 1Extremal and Probabilistic Combinatorics Aula 1 Parte 1
Extremal and Probabilistic Combinatorics In this course we will introduce the student to the basic theorems and proof techniques in extremal graph theory and probabilistic combinatorics. We shall emphasize the close links between these two areas, and provide the background material for modern research fields such as additive combinatorics, monotone and hereditary properties, and graph limits. We also discuss some simple but powerful applications of techniques from functional analysis and linear algebra. The course has no prerequisites. Programa: 1. Ramsey Theory: Finite and infinite versions. Erdös' random proof of the lower bound. Van de -
Counting and Combinatorics in Discrete Math Part 1
Counting and Combinatorics in Discrete Math Part 1Counting and Combinatorics in Discrete Math Part 1
This is part 1 of learning basic counting and combinations in discrete mathematics. I will give some examples to get you introduced to the idea of finding combinations. -
GMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT Prep
GMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT PrepGMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT Prep
http://www.manhattanreview.com/gmat-online/. This video covers the permutation and combinatorics problems in the GMAT Math Problem Solving section. Manhattan... -
How To Do Combinatorics In Poker
How To Do Combinatorics In PokerHow To Do Combinatorics In Poker
http://nitreg.com How do you figure out combinatorics in poker? Watch this video and find out. The math is fairly easy and I show you a couple of examples to... -
Unizor - Combinatorics - Permutations
Unizor - Combinatorics - PermutationsUnizor - Combinatorics - Permutations
Combinatorics is a much newer part of mathematics than such classical subjects as Geometry or Algebra. Very important stimulus to its development was the Theory of Probabilities, which is the next subject in this course. Later on, Game Theory and contemporary Computer Science were the other fields of application of the combinatorics. The subject of Permutations is calculating the number of possibilities of putting certain number of objects in certain order. Examples are numerous. For instance, you have to visit 3 different places A, B and C. The order in which you visit them can be ABC, ACB, BAC, BCA, CAB and CBA. Actually, these 6 differen -
Alexander Postnikov (MIT) The Combinatorics of the Grassmanian I
Alexander Postnikov (MIT) The Combinatorics of the Grassmanian IAlexander Postnikov (MIT) The Combinatorics of the Grassmanian I
Alexander Postnikov (MIT) The Combinatorics of the Grassmanian I -
Combination formula
Combination formulaCombination formula
-
Die rolling probability | Probability and combinatorics | Precalculus | Khan Academy
Die rolling probability | Probability and combinatorics | Precalculus | Khan AcademyDie rolling probability | Probability and combinatorics | Precalculus | Khan Academy
We're thinking about the probability of rolling doubles on a pair of dice. Let's create a grid of all possible outcomes. Watch the next lesson: https://www.khanacademy.org/math/precalculus/prob_comb/independent_events_precalc/v/lebron-asks-about-the-chances-of-making-10-free-throws?utm_source=YT&utm;_medium=Desc&utm;_campaign=Precalculus Missed the previous lesson? https://www.khanacademy.org/math/precalculus/prob_comb/independent_events_precalc/v/getting-at-least-one-heads?utm_source=YT&utm;_medium=Desc&utm;_campaign=Precalculus Precalculus on Khan Academy: You may think that precalculus is simply the course you take before calculus. You wou -
Simple Combinatorics
Simple CombinatoricsSimple Combinatorics
Entity walks through how to quickly and accurately count combinations of hands. This skill will help you understand what hands your opponent is likely to hol... -
Combinatorics: Venn Diagrams and the Inclusion-Exclusion Principle
Combinatorics: Venn Diagrams and the Inclusion-Exclusion PrincipleCombinatorics: Venn Diagrams and the Inclusion-Exclusion Principle
A look at Venn Diagrams and the Inclusion-Exclusion Principle. Includes the solution to a question from Richard G. Brown's "Advanced Mathematics: Precalculus... -
0.4 Analytic Combinatorics 2915)
0.4 Analytic Combinatorics 2915)0.4 Analytic Combinatorics 2915)
-
Basic Combinatorics
Basic CombinatoricsBasic Combinatorics
I created this video with the YouTube Video Editor (http://www.youtube.com/editor) -
Probability using Combinatorics
Probability using CombinatoricsProbability using Combinatorics
-
Combinatorics Problems
Combinatorics ProblemsCombinatorics Problems
-
Introduction to Analytic Combinatorics, Part I with Robert Sedgewick
Introduction to Analytic Combinatorics, Part I with Robert SedgewickIntroduction to Analytic Combinatorics, Part I with Robert Sedgewick
The course "Introduction to Analytic Combinatorics, Part I" by Professor Robert Sedgewick from Princeton University, will be offered free of charge to everyo... -
Permutations and Combinations 1
Permutations and Combinations 1Permutations and Combinations 1
U12_L2_T3_we1 Permutations and Combinations 1 More free lessons at: http://www.khanacademy.org/video?v=oQpKtm5TtxU Content provided by TheNROCproject.org - (...

- Order: Reorder
- Duration: 13:15
- Updated: 26 Apr 2013
- published: 26 Apr 2013
- views: 7529

- Order: Reorder
- Duration: 10:00
- Updated: 11 Aug 2013
- author: khanacademy
- published: 10 Aug 2011
- views: 66399
- author: khanacademy

- Order: Reorder
- Duration: 41:01
- Updated: 03 Jun 2015
- published: 03 Jun 2015
- views: 115

- published: 16 Nov 2012
- views: 4133
- author: eHow
![Combinatorics with Day[9]: Bijections Combinatorics with Day[9]: Bijections](http://web.archive.org./web/20150923164913im_/http://i.ytimg.com/vi/rJmlNIKMVgA/0.jpg)

- Order: Reorder
- Duration: 68:24
- Updated: 18 Aug 2014
- author: Federico Ardila
- published: 30 Aug 2013
- views: 3409
- author: Federico Ardila
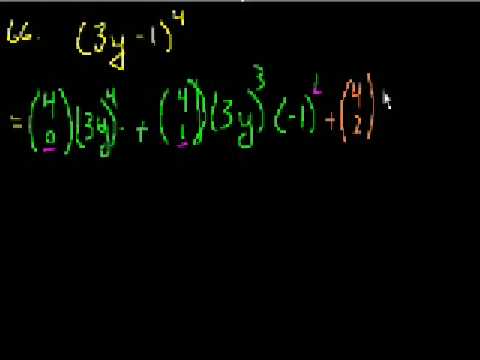
- Order: Reorder
- Duration: 12:49
- Updated: 24 Dec 2008
- published: 24 Dec 2008
- views: 44118

- Order: Reorder
- Duration: 47:42
- Updated: 03 Feb 2015
- published: 03 Feb 2015
- views: 3

- Order: Reorder
- Duration: 10:23
- Updated: 01 Dec 2014
- published: 01 Dec 2014
- views: 7

- Order: Reorder
- Duration: 6:26
- Updated: 07 Aug 2014
- author: ManhattanReview
- published: 28 Dec 2009
- views: 7009
- author: ManhattanReview

- Order: Reorder
- Duration: 20:31
- Updated: 23 Aug 2014
- author: nitregpoker
- published: 12 Nov 2012
- views: 2835
- author: nitregpoker

- Order: Reorder
- Duration: 18:10
- Updated: 12 May 2014
- published: 12 May 2014
- views: 1

- Order: Reorder
- Duration: 89:36
- Updated: 22 Jan 2015
- published: 22 Jan 2015
- views: 40

- Order: Reorder
- Duration: 11:17
- Updated: 21 Nov 2014
http://wn.com/Combination_formula
- published: 21 Nov 2014
- views: 10113

- Order: Reorder
- Duration: 5:15
- Updated: 13 Jul 2015
- published: 13 Jul 2015
- views: 89446

- Order: Reorder
- Duration: 3:56
- Updated: 10 Jun 2013
- author: DeucesCracked
- published: 13 May 2013
- views: 174
- author: DeucesCracked

- Order: Reorder
- Duration: 13:12
- Updated: 30 May 2014
- author: Paul Griffin
- published: 10 Mar 2013
- views: 1672
- author: Paul Griffin

- Order: Reorder
- Duration: 29:16
- Updated: 27 Apr 2014
- author: Wenlong ZHAO
http://wn.com/0.4_Analytic_Combinatorics_2915)

- published: 25 Nov 2013
- views: 525
- author: MrCHSMath

- Order: Reorder
- Duration: 8:28
- Updated: 16 Jan 2013
- author: Catherine Boersma
http://wn.com/Combinatorics_Problems

- Order: Reorder
- Duration: 1:02
- Updated: 01 May 2014
- author: CourseraVideos
- published: 18 Apr 2012
- views: 4053
- author: CourseraVideos

- Order: Reorder
- Duration: 3:45
- Updated: 05 Sep 2014
- author: Khan Academy
- published: 27 Jun 2010
- views: 255892
- author: Khan Academy
- Playlist
- Chat

Getting Exactly Two Heads (Combinatorics)
- published: 10 Aug 2011
- views: 66399
- author: khanacademy

MathHistory29: Combinatorics
- published: 03 Jun 2015
- views: 115

Introduction to Combinatorics : Principles of Math
- published: 16 Nov 2012
- views: 4133
- author: eHow

Lecture 1 . Enumerative Combinatorics (Federico Ardila)
- published: 30 Aug 2013
- views: 3409
- author: Federico Ardila
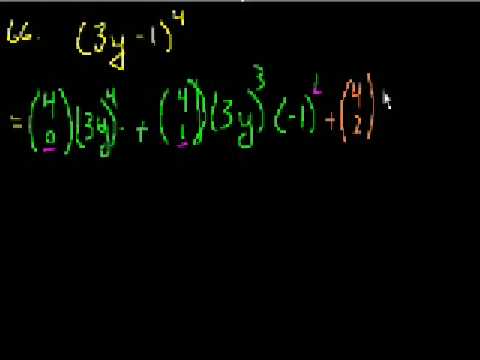
Algebra II: binomial Expansion and Combinatorics
- published: 24 Dec 2008
- views: 44118

Extremal and Probabilistic Combinatorics Aula 1 Parte 1
- published: 03 Feb 2015
- views: 3

Counting and Combinatorics in Discrete Math Part 1
- published: 01 Dec 2014
- views: 7

GMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT Prep
- published: 28 Dec 2009
- views: 7009
- author: ManhattanReview

How To Do Combinatorics In Poker
- published: 12 Nov 2012
- views: 2835
- author: nitregpoker

Unizor - Combinatorics - Permutations
- published: 12 May 2014
- views: 1

Alexander Postnikov (MIT) The Combinatorics of the Grassmanian I
- published: 22 Jan 2015
- views: 40
- 1
- 2
- 3
- 4
- 5
- Next page »
![[u'Probability using Combinatorics'][0].replace('](http://web.archive.org./web/20150923164913im_/http://i.ytimg.com/vi/MlKG4tVk-mY/0.jpg)




