Branches of Mathematics
Pure mathematics
Applied mathematics
- Dynamical systems and differential equations
- Mathematical physics
- Computing
- Information theory and signal processing
- Probability and statistics
- Game theory
- Operations research
Related Topics
- Electromagnetic Spectrum
- Linear Equations
- Applied Physics
- Nano Technology
- Engineering Sciences
- Mathematical Medicine
- Fluid dynamics
- Computational Mathematics
- Gamma Ray Optics
- Onfrared Optics
- Relative Velocity
- Iciam
- Intelligent Imaging Neuroscience
- Biomedical Engineering
- Neuroscience Research
- Quantum Cosmology
- Brain Research
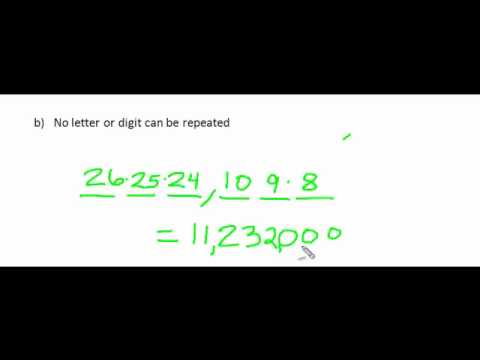



![Combinatorics with Day[9]: Bijections. Combinatorics with Day[9]: Bijections](http://web.archive.org./web/20150627155433im_/http://i.ytimg.com/vi/rJmlNIKMVgA/0.jpg)








Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size (enumerative combinatorics), deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria (as in combinatorial designs and matroid theory), finding "largest", "smallest", or "optimal" objects (extremal combinatorics and combinatorial optimization), and studying combinatorial structures arising in an algebraic context, or applying algebraic techniques to combinatorial problems (algebraic combinatorics).
Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry, and combinatorics also has many applications in optimization, computer science, ergodic theory and statistical physics. Many combinatorial questions have historically been considered in isolation, giving an ad hoc solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics is graph theory, which also has numerous natural connections to other areas. Combinatorics is used frequently in computer science to obtain formulas and estimates in the analysis of algorithms.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...

-
Basic Combinatorics- Part 1
Basic Combinatorics- Part 1 -
Getting Exactly Two Heads (Combinatorics)
Getting Exactly Two Heads (Combinatorics)Getting Exactly Two Heads (Combinatorics)
Learn more: http://www.khanacademy.org/video?v=8TIben0bJpU A different way to think about the probability of getting 2 heads in 4 flips. -
Introduction to Combinatorics : Principles of Math
Introduction to Combinatorics : Principles of MathIntroduction to Combinatorics : Principles of Math
Subscribe Now: http://www.youtube.com/subscription_center?add_user=Ehow Watch More: http://www.youtube.com/Ehow Combinatorics is a very important course in t... -
Lecture 1 . Enumerative Combinatorics (Federico Ardila)
Lecture 1 . Enumerative Combinatorics (Federico Ardila)Lecture 1 . Enumerative Combinatorics (Federico Ardila)
Much of enumerative combinatorics concerns the question: "Count the number a_n of elements of a set S_n for n=1,2,..." We discuss four types of answers: an e... -
Combinatorics with Day[9]: Bijections
Combinatorics with Day[9]: BijectionsCombinatorics with Day[9]: Bijections
Combinatorics with Day[9]: Bijections. -
Basic Combinatorics
Basic CombinatoricsBasic Combinatorics
I created this video with the YouTube Video Editor (http://www.youtube.com/editor) -
Unizor - -Combinatorics - Combinations with Repetitions
Unizor - -Combinatorics - Combinations with RepetitionsUnizor - -Combinatorics - Combinations with Repetitions
In this lecture we will discuss a different type of combinations - the combinations with repetitions. Assume, again, that we have to pick K objects out of a set of N different objects, but after each pick we just record which object we picked and then put it back, so we can pick the same object again repetitively. Now we can have the number of picks K not restricted by the number of objects N, it can be smaller, equal or greater than N. Another, more practical situation of combinations with repetitions can be observed if the number N represents not the total number of objects, but the number of different types of objects with an unlimited nu -
Combinatorics Recurrence Relations Part 1
Combinatorics Recurrence Relations Part 1Combinatorics Recurrence Relations Part 1
The video helps in understanding the concept of Recurrene Relations. -
GMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT Prep
GMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT PrepGMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT Prep
http://www.manhattanreview.com/gmat-online/. This video covers the permutation and combinatorics problems in the GMAT Math Problem Solving section. Manhattan... -
Combinatorics: Venn Diagrams and the Inclusion-Exclusion Principle
Combinatorics: Venn Diagrams and the Inclusion-Exclusion PrincipleCombinatorics: Venn Diagrams and the Inclusion-Exclusion Principle
A look at Venn Diagrams and the Inclusion-Exclusion Principle. Includes the solution to a question from Richard G. Brown's "Advanced Mathematics: Precalculus... -
Counting and Combinatorics in Discrete Math Part 1
Counting and Combinatorics in Discrete Math Part 1Counting and Combinatorics in Discrete Math Part 1
This is part 1 of learning basic counting and combinations in discrete mathematics. I will give some examples to get you introduced to the idea of finding combinations. -
Probability using Combinatorics
Probability using CombinatoricsProbability using Combinatorics
-
Extremal and Probabilistic Combinatorics Aula 1 Parte 1
Extremal and Probabilistic Combinatorics Aula 1 Parte 1Extremal and Probabilistic Combinatorics Aula 1 Parte 1
Extremal and Probabilistic Combinatorics In this course we will introduce the student to the basic theorems and proof techniques in extremal graph theory and probabilistic combinatorics. We shall emphasize the close links between these two areas, and provide the background material for modern research fields such as additive combinatorics, monotone and hereditary properties, and graph limits. We also discuss some simple but powerful applications of techniques from functional analysis and linear algebra. The course has no prerequisites. Programa: 1. Ramsey Theory: Finite and infinite versions. Erdös' random proof of the lower bound. Van de -
Unizor - Combinatorics - Advanced Problems 1.1.
Unizor - Combinatorics - Advanced Problems 1.1.Unizor - Combinatorics - Advanced Problems 1.1.
Problem 1 What is the number of partial permutations of N given objects by K objects under a restriction that each such partial permutation must contain X pa...
- Abstract algebra
- Algebra
- Algebraic geometry
- Algebraic topology
- Analysis
- Ancient history
- Ancient Rome
- Applied mathematics
- Archimedes
- Areas of mathematics
- Arithmetic
- Associahedron
- Astronomer
- Asymptotic analysis
- Automata theory
- Bijective proof
- Binary tree
- Binomial coefficient
- Birkhoff polytope
- Blaise Pascal
- Block design
- Boolean algebras
- Calculus
- Campanology
- Catalan number
- Category theory
- Cayley graph
- Change ringing
- Chromatic polynomial
- Chrysippus
- Coding theory
- Combinations
- Combinatorial design
- Combinatoriality
- Combinatorics
- Complex analysis
- Computer science
- Control theory
- Convex geometry
- Convex polytope
- Countable set
- Decision tree
- Discrete geometry
- Discrete mathematics
- Dynamical system
- Elementary algebra
- Ergodic theory
- Euclidean plane
- Fair division
- Fibonacci numbers
- Finite geometry
- Formal grammar
- Formal language
- Four color problem
- Fractal analysis
- Game theory
- Generating functions
- Geometry
- Gian-Carlo Rota
- Graph coloring
- Graph theory
- Group theory
- Hamiltonian cycle
- Harmonic analysis
- Hasse diagram
- Hassler Whitney
- Hipparchus
- Historian
- Icosahedron
- Inclusion map
- India
- Information theory
- Integer partition
- Isaac Newton
- Ising model
- Jacob Bernoulli
- Kissing number
- Lattice (order)
- Lattice graph
- Leonard Euler
- Levi ben Gerson
- Lie theory
- Linear algebra
- Linear independence
- Linguistics
- Markov chains
- Mathematical logic
- Mathematical physics
- Mathematical problem
- Mathematician
- Mathematics
- MathWorld
- Matroid
- Matroid theory
- Measure theory
- Medieval England
- Metric geometry
- Middle Ages
- Multilinear algebra
- Necklace problem
- Number theory
- Numerical analysis
- Operations research
- Order theory
- Ostomachion
- Partition of a set
- Pascal's triangle
- Paul Erdős
- Permutations
- Permutohedron
- Petersen graph
- Philosopher
- Phylogenetics
- Physician
- Pigeonhole principle
- Plane partition
- Plutarch
- Portal Mathematics
- Potts model
- Power set
- Probabilistic method
- Probability
- Probability theory
- Pure mathematics
- Q-series
- Ramsey theory
- Random graph
- Renaissance
- Richard P. Stanley
- Schröder number
- Science
- Self-avoiding walk
- Set intersection
- Set system
- Set theory
- Special functions
- Statistical physics
- Steiner system
- Sufficiently large
- Sushruta
- Sushruta Samhita
- Talmudist
- Thue-Morse sequence
- Tiling puzzle
- Topology
- Tutte polynomial
- Twelvefold way
- Vector space
- Young diagram
-
Basic Combinatorics- Part 1
Basic Combinatorics- Part 1Basic Combinatorics- Part 1
Introduction to combinations and permutations -
Getting Exactly Two Heads (Combinatorics)
Getting Exactly Two Heads (Combinatorics)Getting Exactly Two Heads (Combinatorics)
Learn more: http://www.khanacademy.org/video?v=8TIben0bJpU A different way to think about the probability of getting 2 heads in 4 flips. -
Introduction to Combinatorics : Principles of Math
Introduction to Combinatorics : Principles of MathIntroduction to Combinatorics : Principles of Math
Subscribe Now: http://www.youtube.com/subscription_center?add_user=Ehow Watch More: http://www.youtube.com/Ehow Combinatorics is a very important course in t... -
Lecture 1 . Enumerative Combinatorics (Federico Ardila)
Lecture 1 . Enumerative Combinatorics (Federico Ardila)Lecture 1 . Enumerative Combinatorics (Federico Ardila)
Much of enumerative combinatorics concerns the question: "Count the number a_n of elements of a set S_n for n=1,2,..." We discuss four types of answers: an e... -
Combinatorics with Day[9]: Bijections
Combinatorics with Day[9]: BijectionsCombinatorics with Day[9]: Bijections
Combinatorics with Day[9]: Bijections. -
Basic Combinatorics
Basic CombinatoricsBasic Combinatorics
I created this video with the YouTube Video Editor (http://www.youtube.com/editor) -
Unizor - -Combinatorics - Combinations with Repetitions
Unizor - -Combinatorics - Combinations with RepetitionsUnizor - -Combinatorics - Combinations with Repetitions
In this lecture we will discuss a different type of combinations - the combinations with repetitions. Assume, again, that we have to pick K objects out of a set of N different objects, but after each pick we just record which object we picked and then put it back, so we can pick the same object again repetitively. Now we can have the number of picks K not restricted by the number of objects N, it can be smaller, equal or greater than N. Another, more practical situation of combinations with repetitions can be observed if the number N represents not the total number of objects, but the number of different types of objects with an unlimited nu -
Combinatorics Recurrence Relations Part 1
Combinatorics Recurrence Relations Part 1Combinatorics Recurrence Relations Part 1
The video helps in understanding the concept of Recurrene Relations. -
GMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT Prep
GMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT PrepGMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT Prep
http://www.manhattanreview.com/gmat-online/. This video covers the permutation and combinatorics problems in the GMAT Math Problem Solving section. Manhattan... -
Combinatorics: Venn Diagrams and the Inclusion-Exclusion Principle
Combinatorics: Venn Diagrams and the Inclusion-Exclusion PrincipleCombinatorics: Venn Diagrams and the Inclusion-Exclusion Principle
A look at Venn Diagrams and the Inclusion-Exclusion Principle. Includes the solution to a question from Richard G. Brown's "Advanced Mathematics: Precalculus... -
Counting and Combinatorics in Discrete Math Part 1
Counting and Combinatorics in Discrete Math Part 1Counting and Combinatorics in Discrete Math Part 1
This is part 1 of learning basic counting and combinations in discrete mathematics. I will give some examples to get you introduced to the idea of finding combinations. -
Probability using Combinatorics
Probability using CombinatoricsProbability using Combinatorics
-
Extremal and Probabilistic Combinatorics Aula 1 Parte 1
Extremal and Probabilistic Combinatorics Aula 1 Parte 1Extremal and Probabilistic Combinatorics Aula 1 Parte 1
Extremal and Probabilistic Combinatorics In this course we will introduce the student to the basic theorems and proof techniques in extremal graph theory and probabilistic combinatorics. We shall emphasize the close links between these two areas, and provide the background material for modern research fields such as additive combinatorics, monotone and hereditary properties, and graph limits. We also discuss some simple but powerful applications of techniques from functional analysis and linear algebra. The course has no prerequisites. Programa: 1. Ramsey Theory: Finite and infinite versions. Erdös' random proof of the lower bound. Van de -
Unizor - Combinatorics - Advanced Problems 1.1.
Unizor - Combinatorics - Advanced Problems 1.1.Unizor - Combinatorics - Advanced Problems 1.1.
Problem 1 What is the number of partial permutations of N given objects by K objects under a restriction that each such partial permutation must contain X pa... -
How To Do Combinatorics In Poker
How To Do Combinatorics In PokerHow To Do Combinatorics In Poker
http://nitreg.com How do you figure out combinatorics in poker? Watch this video and find out. The math is fairly easy and I show you a couple of examples to... -
Combinatorics Problems
Combinatorics ProblemsCombinatorics Problems
-
Enumerative combinatorics
Enumerative combinatoricsEnumerative combinatorics
(C) 2012 David Liao lookatphysics.com CC-BY-SA Permutations and factorials Combinations Binomial theorem Small parameter expansion. -
Intuitive connection between binomial expansion and combinatorics
Intuitive connection between binomial expansion and combinatoricsIntuitive connection between binomial expansion and combinatorics
Description -
GMAT Content: Combinations and Permutations | Kaplan Test Prep
GMAT Content: Combinations and Permutations | Kaplan Test PrepGMAT Content: Combinations and Permutations | Kaplan Test Prep
Combinations and Permutations can be among the hardest of GMAT math concepts. Generally, these rarely-tested concepts aren't worth focusing on until you've m... -
0.4 Analytic Combinatorics 2915)
0.4 Analytic Combinatorics 2915)0.4 Analytic Combinatorics 2915)
-
Alexander Postnikov (MIT) The Combinatorics of the Grassmanian I
Alexander Postnikov (MIT) The Combinatorics of the Grassmanian IAlexander Postnikov (MIT) The Combinatorics of the Grassmanian I
Alexander Postnikov (MIT) The Combinatorics of the Grassmanian I -
Introduction to Analytic Combinatorics, Part I with Robert Sedgewick
Introduction to Analytic Combinatorics, Part I with Robert SedgewickIntroduction to Analytic Combinatorics, Part I with Robert Sedgewick
The course "Introduction to Analytic Combinatorics, Part I" by Professor Robert Sedgewick from Princeton University, will be offered free of charge to everyo... -
Combinatorics: N choose K, permutations and subsets
Combinatorics: N choose K, permutations and subsetsCombinatorics: N choose K, permutations and subsets
Why is n-choose-k the correct way to count stuff.
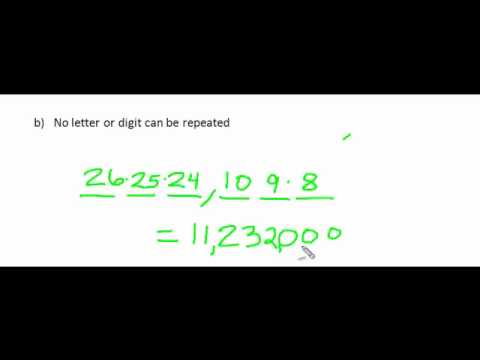
- Order: Reorder
- Duration: 13:15
- Updated: 26 Apr 2013
- published: 26 Apr 2013
- views: 7529

- Order: Reorder
- Duration: 10:00
- Updated: 11 Aug 2013
- author: khanacademy
- published: 10 Aug 2011
- views: 66399
- author: khanacademy

- published: 16 Nov 2012
- views: 4133
- author: eHow

- Order: Reorder
- Duration: 68:24
- Updated: 18 Aug 2014
- author: Federico Ardila
- published: 30 Aug 2013
- views: 3409
- author: Federico Ardila
![Combinatorics with Day[9]: Bijections Combinatorics with Day[9]: Bijections](http://web.archive.org./web/20150627155433im_/http://i.ytimg.com/vi/rJmlNIKMVgA/0.jpg)

- published: 25 Nov 2013
- views: 525
- author: MrCHSMath

- Order: Reorder
- Duration: 23:03
- Updated: 19 May 2014
- published: 19 May 2014
- views: 447

- Order: Reorder
- Duration: 57:22
- Updated: 24 Jun 2013
- author: Complete GATE
- published: 24 Jun 2013
- views: 18
- author: Complete GATE

- Order: Reorder
- Duration: 6:26
- Updated: 07 Aug 2014
- author: ManhattanReview
- published: 28 Dec 2009
- views: 7009
- author: ManhattanReview

- Order: Reorder
- Duration: 13:12
- Updated: 30 May 2014
- author: Paul Griffin
- published: 10 Mar 2013
- views: 1672
- author: Paul Griffin

- Order: Reorder
- Duration: 10:23
- Updated: 01 Dec 2014
- published: 01 Dec 2014
- views: 7

- Order: Reorder
- Duration: 47:42
- Updated: 03 Feb 2015
- published: 03 Feb 2015
- views: 3

- Order: Reorder
- Duration: 21:22
- Updated: 11 Aug 2014
- author: Zor Shekhtman
- published: 24 May 2014
- views: 52
- author: Zor Shekhtman

- Order: Reorder
- Duration: 20:31
- Updated: 23 Aug 2014
- author: nitregpoker
- published: 12 Nov 2012
- views: 2835
- author: nitregpoker

- Order: Reorder
- Duration: 8:28
- Updated: 16 Jan 2013
- author: Catherine Boersma
http://wn.com/Combinatorics_Problems

- Order: Reorder
- Duration: 13:29
- Updated: 25 Aug 2014
- author: lookatphysics
- published: 14 Jul 2012
- views: 961
- author: lookatphysics

- Order: Reorder
- Duration: 4:15
- Updated: 27 Mar 2014
- published: 27 Mar 2014
- views: 2087

- Order: Reorder
- Duration: 6:23
- Updated: 06 Aug 2013
- author: KaplanGMAT
- published: 15 Apr 2010
- views: 3494
- author: KaplanGMAT

- Order: Reorder
- Duration: 29:16
- Updated: 27 Apr 2014
- author: Wenlong ZHAO
http://wn.com/0.4_Analytic_Combinatorics_2915)

- Order: Reorder
- Duration: 89:36
- Updated: 22 Jan 2015
- published: 22 Jan 2015
- views: 40

- Order: Reorder
- Duration: 1:02
- Updated: 01 May 2014
- author: CourseraVideos
- published: 18 Apr 2012
- views: 4053
- author: CourseraVideos

- Order: Reorder
- Duration: 5:37
- Updated: 15 Jul 2013
- author: Professor Elvis Zap
- published: 22 Apr 2010
- views: 7721
- author: Professor Elvis Zap
- Playlist
- Chat

Getting Exactly Two Heads (Combinatorics)
Learn more: http://www.khanacademy.org/video?v=8TIben0bJpU A different way to think about the probability of getting 2 heads in 4 flips.- published: 10 Aug 2011
- views: 66399
- author: khanacademy

Introduction to Combinatorics : Principles of Math
Subscribe Now: http://www.youtube.com/subscription_center?add_user=Ehow Watch More: http://www.youtube.com/Ehow Combinatorics is a very important course in t...- published: 16 Nov 2012
- views: 4133
- author: eHow

Lecture 1 . Enumerative Combinatorics (Federico Ardila)
Much of enumerative combinatorics concerns the question: "Count the number a_n of elements of a set S_n for n=1,2,..." We discuss four types of answers: an e...- published: 30 Aug 2013
- views: 3409
- author: Federico Ardila

Basic Combinatorics
I created this video with the YouTube Video Editor (http://www.youtube.com/editor)- published: 25 Nov 2013
- views: 525
- author: MrCHSMath

Unizor - -Combinatorics - Combinations with Repetitions
In this lecture we will discuss a different type of combinations - the combinations with repetitions. Assume, again, that we have to pick K objects out of a set of N different objects, but after each pick we just record which object we picked and then put it back, so we can pick the same object again repetitively. Now we can have the number of picks K not restricted by the number of objects N, it can be smaller, equal or greater than N. Another, more practical situation of combinations with repetitions can be observed if the number N represents not the total number of objects, but the number of different types of objects with an unlimited number of objects of each type (so, we don't have to return back our pick to facilitate the repetition). Now our task is to pick K objects, and combinations we pick differ only by their composition, that is the number of objects of each type. For example, we came to a store to buy some wine. We would like to pick the total of K=5 bottles and we have N=3 types of wine we want - red, white and sparkling. The question is, how many different combinations of these three types of wine we can choose in a set of five bottles, assuming the store has sufficient supply of each type. As in the case of regular combinations, let's come up with some clever logical procedure to resolve this problem. We will use the wine example above to illustrate it. Let's use a letter W to indicate a bottle of wine and a slash / to separate wines of different types. For instance, we picked 1 red, 1 white and 3 sparkling wines. Then we can form a string that represents our purchase as follows: W/W/WWW Analogously, string /WWWWW/ indicates our pick of five bottles of white wine, string //WWWWW indicates a purchase of five bottles of sparkling wine, string WW/WW/W indicates a purchase of two red, two white and one sparking wine bottles. As we see, our pick is fully defined by these strings and the total number of different combinations is the total number of different strings of seven characters with five W's and two slashes. Since the difference between strings is only in the position of two slashes among seven characters, each string can be obtained by just picking two different numbers out of numbers from 1 to 7 and call the characters with these numbers "a type separator - slash", while the characters at other positions will be called "wine bottle - W". Therefore, the total number of our combinations with repetitions equals to a number of regular combinations of 2 objects of a set of 7 different objects: C(7,2) = 7! / (2!·5!) = 21. Incidentally, instead of picking the positions of two slashes, we can equally say that our pick is fully defined by the positions of five characters W. That leads to a number of regular combinations of five objects out of a set of seven different objects with a formula C(7,2) = 7! / (5!·2!) = 21. This is exactly the same as above, which should be of no surprise for us since the formula for regular combinations is symmetrical relative to a subset of chosen objects and a subset of remaining ones. Let's generalize this logic. We have N types of objects and unlimited number of objects of each type. We pick K objects out of them. How many different combinations of types (compositions of our set of picked objects) can be picked? Following the same logic and symbolics, let's imagine strings containing K characters W signifying a picked objects and N−1 type separators - slashes /. The length of each string is K+N−1. Each such string represents a particular composition of a set of picked objects by their types. So, the position of slashes (or, as we mentioned above, the position of W's) fully define the composition of a set of picked objects. The number of different strings of this kind is the number of regular combinations of N−1 objects out of K+N−1 or, equally, the number of regular combinations of K objects out of K+N−1: C(K+N−1,N−1) = = C(K+N−1,K) = = (K+N−1)! / [K!·(N−1)!] Let's consider a couple of simple examples to check this formula. Example 1: The number of object types N equals to 1. In this case we have only one choice to pick K objects - all objects are of that one and only type. The formula gives (K+1−1)! / [K!·(1−1)!] = = K! / (K!·0!) = 1 as is supposed to be. Example 2: The number of object types N equals to 2. In this case we can pick K objects by choosing 0 objects of the first type and K objects of the second type or 1 object of the first type and K−1 objects of the second type etc. up to K objects of the first type and 0 objects of the second type. The number of choices is K+1. The formula gives (K+2−1)! / [K!·(2−1)!] = = (K+1)! / [K!·1!] = = (K+1)! / K! = K+1 as is supposed to be.- published: 19 May 2014
- views: 447

Combinatorics Recurrence Relations Part 1
The video helps in understanding the concept of Recurrene Relations.- published: 24 Jun 2013
- views: 18
- author: Complete GATE

GMAT Online Math - Permutation & Combinatorics 1 | Manhattan Review GMAT Prep
http://www.manhattanreview.com/gmat-online/. This video covers the permutation and combinatorics problems in the GMAT Math Problem Solving section. Manhattan...- published: 28 Dec 2009
- views: 7009
- author: ManhattanReview

Combinatorics: Venn Diagrams and the Inclusion-Exclusion Principle
A look at Venn Diagrams and the Inclusion-Exclusion Principle. Includes the solution to a question from Richard G. Brown's "Advanced Mathematics: Precalculus...- published: 10 Mar 2013
- views: 1672
- author: Paul Griffin

Counting and Combinatorics in Discrete Math Part 1
This is part 1 of learning basic counting and combinations in discrete mathematics. I will give some examples to get you introduced to the idea of finding combinations.- published: 01 Dec 2014
- views: 7

Extremal and Probabilistic Combinatorics Aula 1 Parte 1
Extremal and Probabilistic Combinatorics In this course we will introduce the student to the basic theorems and proof techniques in extremal graph theory and probabilistic combinatorics. We shall emphasize the close links between these two areas, and provide the background material for modern research fields such as additive combinatorics, monotone and hereditary properties, and graph limits. We also discuss some simple but powerful applications of techniques from functional analysis and linear algebra. The course has no prerequisites. Programa: 1. Ramsey Theory: Finite and infinite versions. Erdös' random proof of the lower bound. Van der Waarden's Theorem. Statement of Szemerédi's Theorem. 2. Extremal Graph Theory: The theorems of Turán, Erdös-Stone and Kovari-Sós-Turán. 3. The Erdös-Renyi Random Graph: Graphs with high girth and chromatic number. Extremal number of C2k. 1st and 2nd moment methods. Janson's inequality. The giant component. 4. Analytic and Algebraic Methods: The Kneser graph and the Borsuk-Ulam Theorem. The Frankl-Wilson inequality and Borsuk's Conjecture. 5. The Szemerédi Regularity Lemma: Statement and applications, e.g., proof of Erdös-Stone, Erdös-Frankl-Rödl. Proof of Roth's Theorem via the triangle-removal lemma. 6. Dependent Random Choice: Applications, including the proof of the Balog-Szemerédi-Gowers Theorem. Robert Morris- published: 03 Feb 2015
- views: 3

Unizor - Combinatorics - Advanced Problems 1.1.
Problem 1 What is the number of partial permutations of N given objects by K objects under a restriction that each such partial permutation must contain X pa...- published: 24 May 2014
- views: 52
- author: Zor Shekhtman
- 1
- 2
- 3
- 4
- 5
- Next page »





