- published: 11 Sep 2018
- views: 35584

Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.
History
Geometric topology as an area distinct from algebraic topology may be said to have originated in the 1935 classification of lens spaces by Reidemeister torsion, which required distinguishing spaces that are homotopy equivalent but not homeomorphic. This was the origin of simple homotopy theory.
Differences between low-dimensional and high-dimensional topology
Manifolds differ radically in behavior in high and low dimension.
High-dimensional topology refers to manifolds of dimension 5 and above, or in relative terms, embeddings in codimension 3 and above. Low-dimensional topology is concerned with questions in dimensions up to 4, or embeddings in codimension up to 2.
Dimension 4 is special, in that in some respects (topologically), dimension 4 is high-dimensional, while in other respects (differentiably), dimension 4 is low-dimensional; this overlap yields phenomena exceptional to dimension 4, such as exotic differentiable structures on R4. Thus the topological classification of 4-manifolds is in principle easy, and the key questions are: does a topological manifold admit a differentiable structure, and if so, how many? Notably, the smooth case of dimension 4 is the last open case of the generalized Poincaré conjecture; see Gluck twists.
Geometric topology (object)
In mathematics, the geometric topology is a topology one can put on the set H of hyperbolic 3-manifolds of finite volume.
Use
Convergence in this topology is a crucial ingredient of hyperbolic Dehn surgery, a fundamental tool in the theory of hyperbolic 3-manifolds.
Definition
The following is a definition due to Troels Jorgensen:
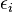 converging to 0, and
converging to 0, and  -bi-Lipschitz diffeomorphisms
-bi-Lipschitz diffeomorphisms 
Alternate definition
There is an alternate definition due to Mikhail Gromov. Gromov's topology utilizes the Gromov-Hausdorff metric and is defined on pointed hyperbolic 3-manifolds. One essentially considers better and better bi-Lipschitz homeomorphisms on larger and larger balls. This results in the same notion of convergence as above as the thick part is always connected; thus, a large ball will eventually encompass all of the thick part.
On framed manifolds
As a further refinement, Gromov's metric can also be defined on framed hyperbolic 3-manifolds. This gives nothing new but this space can be explicitly identified with torsion-free Kleinian groups with the Chabauty topology.
Geometric topology (disambiguation)
In mathematics, the phrase geometric topology may refer to:
Podcasts:
-

Relating Topology and Geometry - 2 Minute Math with Jacob Lurie
Many believe the mathematical fields of Algebraic Topology and Algebraic Geometry are totally unrelated, but Harvard Professor Jacob Lurie delights in finding the connections. Hear about his work at the leading edge of mathematics. Professor Jacob Lurie visited the Fields Institute for the Séminaire de mathématiques supérieures (SMS) 2018 from June 11 to June 15, 2018. The Fields Institute is a centre for mathematical research activity - a place where mathematicians from Canada and abroad, from academia, business, industry and financial institutions, can come together to carry out research and formulate problems of mutual interest. Our mission is to provide a supportive and stimulating environment for mathematics innovation and education. For more on the amazing mathematical research we...
published: 11 Sep 2018 -

Algebra, Geometry, and Topology: What's The Difference?
This Math-Dance video aims to describe how the fields of mathematics are different. Focusing on Algebra, Geometry, and Topology, we use dance to describe how each one of these fields would study a circle. The geometer dances with a rigid hula hoop, the topologist dances with a loop of fabric, and the algebraist dances with a circle of lasers. Written and Created by: Nancy Scherich Filmed and edited by : Alex Nye Produced by: Steven Deeble And Nancy Scherich First Assistant Camera: Chitoh Yung Choreographed by: Nancy Scherich, in collaboration with Katelyn Carano, Erika Walther, Steve Trettel Original Music by Whetzel "This Is What Topology Sounds Like" jameswhetzel.com Cast: Eric Boesser, Nic Brody, Christian Bueno, Katelyn Carano, Michelle Chu, Olivia Davi, Ken Millett, Erin Morg...
published: 15 Feb 2019 -

Who cares about topology? (Inscribed rectangle problem)
An unsolved conjecture, and a clever topological solution to a similar question. Help fund future projects: https://www.patreon.com/3blue1brown An equally valuable form of support is to simply share some of the videos. Special thanks to these supporters: http://3b1b.co/topology-thanks Home page: https://www.3blue1brown.com/ This video is based on a proof from H. Vaughan, 1977. To learn more, take a look at this survey: https://pure.mpg.de/rest/items/item_3120610/component/file_3120611/content Thanks to these viewers for their contributions to translations Hebrew: Omer Tuchfeld ------------------ 3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the b...
published: 04 Nov 2016 -

What is...geometric topology?
Goal. Explaining basic concepts of geometric topology in an intuitive way. This time. What is...geometric topology? Or: It’s a disc! Disclaimer. Nobody is perfect, and I might have said something silly. If there is any doubt, then please check the references. Disclaimer. Geometric topology is usually the study of manifolds. This can mean manifold things ;-) So to be precise, this video series is mostly about knots, surfaces, three and four manifolds. Slides. http://www.dtubbenhauer.com/youtube.html Website with exercises. http://www.dtubbenhauer.com/lecture-geotop-2022.html Thumbnail. https://upload.wikimedia.org/wikipedia/commons/4/47/Torus.svg Geometric topology. https://en.wikipedia.org/wiki/Geometric_topology https://en.wikipedia.org/wiki/List_of_geometric_topology_topics ht...
published: 06 Aug 2022 -

The Biggest Ideas in the Universe | 13. Geometry and Topology
The Biggest Ideas in the Universe is a series of videos where I talk informally about some of the fundamental concepts that help us understand our natural world. Exceedingly casual, not overly polished, and meant for absolutely everybody. This is Idea #13, "Geometry and Topology." Yes that's two ideas, and furthermore they're from math more than from science, but we'll put them to good use. In particular we look at Riemannian (non-Euclidean) geometry, and a kind of topological invariants called "homotopy groups." My web page: http://www.preposterousuniverse.com/ My YouTube channel: https://www.youtube.com/c/seancarroll Mindscape podcast: http://www.preposterousuniverse.com/podcast The Biggest Ideas playlist: https://www.youtube.com/playlist?list=PLrxfgDEc2NxZJcWcrxH3jyjUUrJlnoyzX Blo...
published: 16 Jun 2020 -

Cellular decomposition | Geometric topology
Suborno Isaac is the World's Youngest AIME Qualifier in US Math Olympiad. Link, https://www.brooklyn.edu/bc-news/president-michelle-j-anderson-meets-11-year-old-brooklyn-college-student-suborno-isaac-bari/ Email: suborno.bari@stonybrook.edu
published: 05 Mar 2024 -

Infinite Groups in Geometric Topology, Part 1
This is the first in a series of three one-hour talks delivered by Principal Speaker Kevin Whyte of the University of Illinois at Chicago at the 31st Annual Workshop in Geometric Topology held at the University of Wisconsin-Milwaukee on the dates of June 12-14, 2014.
published: 16 Jul 2014 -

Geometry Topology
published: 23 Sep 2020 -

What is a manifold?
A visual explanation and definition of manifolds are given. This includes motivations for topology, Hausdorffness and second-countability. If you want to learn more, check out one of these (or any other basic differential geometry or topology book): - M. Spivak: "A Comprehensive Introduction to Differential Geometry" - M. Nakahara: "Geometry, Topology and Physics" - J. W. Milnor: "Topology from the differentiable viewpoint"
published: 11 Oct 2015 -

Clifford Torus || Geometric Topology
Clifford Torus || Geometric Topology
published: 02 Jan 2024

Relating Topology and Geometry - 2 Minute Math with Jacob Lurie
- Order: Reorder
- Duration: 2:19
- Uploaded Date: 11 Sep 2018
- views: 35584

Algebra, Geometry, and Topology: What's The Difference?
- Order: Reorder
- Duration: 3:01
- Uploaded Date: 15 Feb 2019
- views: 46484
- published: 15 Feb 2019
- views: 46484

Who cares about topology? (Inscribed rectangle problem)
- Order: Reorder
- Duration: 18:16
- Uploaded Date: 04 Nov 2016
- views: 3216079
- published: 04 Nov 2016
- views: 3216079

What is...geometric topology?
- Order: Reorder
- Duration: 16:38
- Uploaded Date: 06 Aug 2022
- views: 4625
- published: 06 Aug 2022
- views: 4625

The Biggest Ideas in the Universe | 13. Geometry and Topology
- Order: Reorder
- Duration: 1:26:09
- Uploaded Date: 16 Jun 2020
- views: 156682
- published: 16 Jun 2020
- views: 156682

Cellular decomposition | Geometric topology
- Order: Reorder
- Duration: 2:47
- Uploaded Date: 05 Mar 2024
- views: 27362
- published: 05 Mar 2024
- views: 27362

Infinite Groups in Geometric Topology, Part 1
- Order: Reorder
- Duration: 58:08
- Uploaded Date: 16 Jul 2014
- views: 2220
- published: 16 Jul 2014
- views: 2220

Geometry Topology
- Order: Reorder
- Duration: 21:35
- Uploaded Date: 23 Sep 2020
- views: 78
- published: 23 Sep 2020
- views: 78

What is a manifold?
- Order: Reorder
- Duration: 3:51
- Uploaded Date: 11 Oct 2015
- views: 211842
- published: 11 Oct 2015
- views: 211842

Clifford Torus || Geometric Topology
- Order: Reorder
- Duration: 0:11
- Uploaded Date: 02 Jan 2024
- views: 1097
- published: 02 Jan 2024
- views: 1097



Relating Topology and Geometry - 2 Minute Math with Jacob Lurie
- Report rights infringement
- published: 11 Sep 2018
- views: 35584

Algebra, Geometry, and Topology: What's The Difference?
- Report rights infringement
- published: 15 Feb 2019
- views: 46484

Who cares about topology? (Inscribed rectangle problem)
- Report rights infringement
- published: 04 Nov 2016
- views: 3216079

What is...geometric topology?
- Report rights infringement
- published: 06 Aug 2022
- views: 4625

The Biggest Ideas in the Universe | 13. Geometry and Topology
- Report rights infringement
- published: 16 Jun 2020
- views: 156682

Cellular decomposition | Geometric topology
- Report rights infringement
- published: 05 Mar 2024
- views: 27362

Infinite Groups in Geometric Topology, Part 1
- Report rights infringement
- published: 16 Jul 2014
- views: 2220

What is a manifold?
- Report rights infringement
- published: 11 Oct 2015
- views: 211842

Clifford Torus || Geometric Topology
- Report rights infringement
- published: 02 Jan 2024
- views: 1097

Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.
History
Geometric topology as an area distinct from algebraic topology may be said to have originated in the 1935 classification of lens spaces by Reidemeister torsion, which required distinguishing spaces that are homotopy equivalent but not homeomorphic. This was the origin of simple homotopy theory.
Differences between low-dimensional and high-dimensional topology
Manifolds differ radically in behavior in high and low dimension.
High-dimensional topology refers to manifolds of dimension 5 and above, or in relative terms, embeddings in codimension 3 and above. Low-dimensional topology is concerned with questions in dimensions up to 4, or embeddings in codimension up to 2.
Dimension 4 is special, in that in some respects (topologically), dimension 4 is high-dimensional, while in other respects (differentiably), dimension 4 is low-dimensional; this overlap yields phenomena exceptional to dimension 4, such as exotic differentiable structures on R4. Thus the topological classification of 4-manifolds is in principle easy, and the key questions are: does a topological manifold admit a differentiable structure, and if so, how many? Notably, the smooth case of dimension 4 is the last open case of the generalized Poincaré conjecture; see Gluck twists.
Latest News for: geometric topology
Webinar on Popularizing Mathematics and Science to be held on Jan 15
The world's most fascinating transport maps: From London to Paris and New York to Mexico, ...
Weeks after retirement, Lehigh professor leads teens to national math win
 The Morning Call
09 Jul 2024
The Morning Call
09 Jul 2024
New theory links quantum geometry to electron-phonon coupling
Researchers engineer new approach for controlling thermal emission
Tailoring electron vortex beams with customizable intensity patterns by electron diffraction holography
Physicists discover a novel quantum state in an elemental solid
Research team establishes synthetic dimension dynamics to manipulate light
When the music changes, so does the dance: Controlling cooperative electronic states in kagome metals
Scientists discover exotic quantum interference effect in a topological insulator device
Sub-wavelength confinement of light demonstrated in indium phosphide nanocavity
Widely accepted Weyl semimetal shown to be a magnetic semiconductor
Team discovers thousands of new transformable knots
Pills From The 3D Printer
Global symmetry found to be not completely necessary for the protection of topological boundary states
- 1
- 2
- Next page »
