Latest News for: lorenz attractor
Edit
Scientists demonstrate chemical reservoir computation using the formose reaction
Phys Dot Org 13 Jul 2024
Wilhelm Huck from Radboud University ... Prof ... Furthermore, the system demonstrated the ability to forecast future states of a chaotic system (the Lorenz attractor), accurately predicting two out of three input dimensions several hours into the future.
Edit
REVIEW: The Psychology of Totalitarianism
Off Guardian 04 Feb 2023
He describes the Lorenz strange attractor in which the rate of change of three variables related to a moving water wheel are graphed over time, revealing a pattern that has been used to demonstrate sensitive dependence on initial conditions (i.e.
- 1


 ,
, 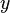 , and
, and  make up the system state,
make up the system state, 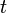 is time, and
is time, and  ,
, 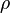 ,
, 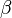 are the system parameters. The Lorenz equations also arise in simplified models for
are the system parameters. The Lorenz equations also arise in simplified models for 