- published: 26 Oct 2023
- views: 6652

Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics. It asserts that the phase-space distribution function is constant along the trajectories of the system — that is that the density of system points in the vicinity of a given system point traveling through phase-space is constant with time.
There are related mathematical results in symplectic topology and ergodic theory.
Liouville equations
The Liouville equation describes the time evolution of the phase space distribution function. Although the equation is usually referred to as the "Liouville equation", Josiah Willard Gibbs was the first to recognize the importance of this equation as the fundamental equation of statistical mechanics. It is referred to as the Liouville equation because its derivation for non-canonical systems utilises an identity first derived by Liouville in 1838.
Consider a Hamiltonian dynamical system with canonical coordinates  and conjugate momenta
and conjugate momenta  , where
, where  . Then the phase space distribution
. Then the phase space distribution  determines the probability
determines the probability  that the system will be found in the infinitesimal phase space volume
that the system will be found in the infinitesimal phase space volume 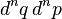 . The Liouville equation governs the evolution of
. The Liouville equation governs the evolution of  in time
in time  :
:
Liouville's theorem
Liouville's theorem has various meanings, all mathematical results named after Joseph Liouville:
- There is also a related theorem on harmonic functions
Liouville's theorem (conformal mappings)
In mathematics, Liouville's theorem, proved by Joseph Liouville in 1850, is a rigidity theorem about conformal mappings in Euclidean space. It states that any smooth conformal mapping on a domain of Rn, where n > 2, can be expressed as a composition of translations, similarities, orthogonal transformations and inversions: they are Möbius transformations (in n dimensions). This theorem severely limits the variety of possible conformal mappings in R3 and higher-dimensional spaces. By contrast, conformal mappings in R2 can be much more complicated – for example, all simply connected planar domains are conformally equivalent, by the Riemann mapping theorem.
Generalizations of the theorem hold for transformations that are only weakly differentiable (Iwaniec & Martin 2001, Chapter 5). The focus of such a study is the non-linear Cauchy–Riemann system that is a necessary and sufficient condition for a smooth mapping ƒ → Ω → Rn to be conformal:
where Df is the Jacobian derivative, T is the matrix transpose, and I is the identity matrix. A weak solution of this system is defined to be an element ƒ of the Sobolev space W1,n
loc(Ω,Rn) with non-negative Jacobian determinant almost everywhere, such that the Cauchy–Riemann system holds at almost every point of Ω. Liouville's theorem is then that every weak solution (in this sense) is a Möbius transformation, meaning that it has the form
Liouville's theorem (differential algebra)
In mathematics, Liouville's theorem, originally formulated by Joseph Liouville in the 1830s and 1840s, places an important restriction on antiderivatives that can be expressed as elementary functions.
The antiderivatives of certain elementary functions cannot themselves be expressed as elementary functions. A standard example of such a function is  whose antiderivative is (with a multiplier of a constant) the error function, familiar from statistics. Other examples include the functions
whose antiderivative is (with a multiplier of a constant) the error function, familiar from statistics. Other examples include the functions 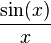 and
and  .
.
Liouville's theorem states that elementary antiderivatives, if they exist, must be in the same differential field as the function, plus possibly a finite number of logarithms.
Definitions
For any differential field F, there is a subfield
called the constants of F. Given two differential fields F and G, G is called a logarithmic extension of F if G is a simple transcendental extension of F (i.e. G = F(t) for some transcendental t) such that
This has the form of a logarithmic derivative. Intuitively, one may think of t as the logarithm of some element s of F, in which case, this condition is analogous to the ordinary chain rule. But it must be remembered that F is not necessarily equipped with a unique logarithm; one might adjoin many "logarithm-like" extensions to F. Similarly, an exponential extension is a simple transcendental extension that satisfies
Podcasts:
-

Phase space & Liouville's Theorem
Hamiltonian dynamics exists in phase space -- a space of formed of all the generalized positions and generalized momenta. We explore ways to solve Hamilton's equations in this space. Music "Everything" by Vi Hart https://soundcloud.com/vihartvihart
published: 26 Oct 2023 -

Hamiltonian Mechanics: Liouville's theorem
Introduction to Classical Mechanics (12 Weeks course) Prof. Anurag Tripathi IIT Hyderabad https://onlinecourses.nptel.ac.in/noc20_ph17/preview
published: 21 Dec 2020 -

Liouville's Theorem
published: 10 Nov 2018 -

Hamiltonian Mechanics for Projectile Motion (plus the Liouville Theorem)
Here is an example of Hamiltonian mechanics for projectile motion.
published: 28 Apr 2023 -

Liouville's theorem (Hamiltonian)
If you find our videos helpful you can support us by buying something from amazon. https://www.amazon.com/?tag=wiki-audio-20 Liouville's theorem (Hamiltonian) In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics.It asserts that the phase-space distribution function is constant along the trajectories of the system — that is that the density of system points in the vicinity of a given system point traveling through phase-space is constant with time. -Video is targeted to blind users Attribution: Article text available under CC-BY-SA image source in video https://www.youtube.com/watch?v=oZi_LyqmceY
published: 22 Jan 2016 -

Classical Mechanics, Lecture 19: Hamiltonian Evolution on Phase Space. Liouville's Theorem.
Lecture 19 of my Classical Mechanics course at McGill University, Winter 2010. Hamiltonian Evolution on Phase Space. Liouville's Theorem. The course webpage, including links to other lectures and problem sets, is available at http://www.physics.mcgill.ca/~maloney/451/ The written notes for this lecture are available at http://www.physics.mcgill.ca/~maloney/451/451-19.pdf
published: 09 Dec 2014 -

Hamiltonian Formalism (3c): Liouville's Theorem
Hamiltonian Formalism: Liouville's Theorem Lectures held at Nous Academy of Theoretical Physics (NATPHYS) https://natphys.net masud naaseri فرمالیسم همیلتونی قضیه لیوویل درس ارائه شده در آکادمی ناصری، پاییز 1394 مسعود ناصری
published: 10 Dec 2015 -

Simple proof of Liouville's theorem
Liouville’s theorem states that the volume of a region in phase space remains constant. The picture shows the formal steps of the mathematical proof. Feel free to check advanced scientific courses here: https://stemabilities.com/collections/frontpage #einstein #math #physics #mathlover #physicslover #physicschallenge #mathchallenge #liouville #lagrange #lagrangian
published: 02 Jun 2022 -

Hamiltonian Formalism (3a): Liouville's Theorem (in Persian)
Hamiltonian Formalism: Liouville's Theorem Lectures held at Nous Academy of Theoretical Physics (NATPHYS) https://natphys.net masud naaseri فرمالیسم همیلتونی قضیه لیوویل درس ارائه شده در آکادمی ناصری، پاییز 1394 مسعود ناصری
published: 10 Dec 2015 -

Liouville's theorem (Hamiltonian) | Wikipedia audio article
This is an audio version of the Wikipedia Article: https://en.wikipedia.org/wiki/Liouville%27s_theorem_(Hamiltonian) 00:00:46 1 Liouville equations 00:11:41 2 Other formulations 00:11:51 2.1 Poisson bracket 00:14:13 2.2 Ergodic theory 00:15:12 2.3 Symplectic geometry 00:16:23 2.4 Quantum Liouville equation 00:18:46 3 Remarks 00:19:46 4 See also Listening is a more natural way of learning, when compared to reading. Written language only began at around 3200 BC, but spoken language has existed long ago. Learning by listening is a great way to: - increases imagination and understanding - improves your listening skills - improves your own spoken accent - learn while on the move - reduce eye strain Now learn the vast amount of general knowledge available on Wikipedia thro...
published: 28 Dec 2018

Phase space & Liouville's Theorem
- Order: Reorder
- Duration: 10:59
- Uploaded Date: 26 Oct 2023
- views: 6652

Hamiltonian Mechanics: Liouville's theorem
- Order: Reorder
- Duration: 53:51
- Uploaded Date: 21 Dec 2020
- views: 10010
- published: 21 Dec 2020
- views: 10010

Liouville's Theorem
- Order: Reorder
- Duration: 12:43
- Uploaded Date: 10 Nov 2018
- views: 18309
- published: 10 Nov 2018
- views: 18309

Hamiltonian Mechanics for Projectile Motion (plus the Liouville Theorem)
- Order: Reorder
- Duration: 24:23
- Uploaded Date: 28 Apr 2023
- views: 1414
- published: 28 Apr 2023
- views: 1414

Liouville's theorem (Hamiltonian)
- Order: Reorder
- Duration: 6:05
- Uploaded Date: 22 Jan 2016
- views: 7823
- published: 22 Jan 2016
- views: 7823

Classical Mechanics, Lecture 19: Hamiltonian Evolution on Phase Space. Liouville's Theorem.
- Order: Reorder
- Duration: 1:20:27
- Uploaded Date: 09 Dec 2014
- views: 6850
- published: 09 Dec 2014
- views: 6850

Hamiltonian Formalism (3c): Liouville's Theorem
- Order: Reorder
- Duration: 42:57
- Uploaded Date: 10 Dec 2015
- views: 533
- published: 10 Dec 2015
- views: 533

Simple proof of Liouville's theorem
- Order: Reorder
- Duration: 4:35
- Uploaded Date: 02 Jun 2022
- views: 793
- published: 02 Jun 2022
- views: 793

Hamiltonian Formalism (3a): Liouville's Theorem (in Persian)
- Order: Reorder
- Duration: 38:17
- Uploaded Date: 10 Dec 2015
- views: 437
- published: 10 Dec 2015
- views: 437

Liouville's theorem (Hamiltonian) | Wikipedia audio article
- Order: Reorder
- Duration: 20:07
- Uploaded Date: 28 Dec 2018
- views: 105
- published: 28 Dec 2018
- views: 105



Phase space & Liouville's Theorem
- Report rights infringement
- published: 26 Oct 2023
- views: 6652

Hamiltonian Mechanics: Liouville's theorem
- Report rights infringement
- published: 21 Dec 2020
- views: 10010

Hamiltonian Mechanics for Projectile Motion (plus the Liouville Theorem)
- Report rights infringement
- published: 28 Apr 2023
- views: 1414

Liouville's theorem (Hamiltonian)
- Report rights infringement
- published: 22 Jan 2016
- views: 7823

Classical Mechanics, Lecture 19: Hamiltonian Evolution on Phase Space. Liouville's Theorem.
- Report rights infringement
- published: 09 Dec 2014
- views: 6850

Hamiltonian Formalism (3c): Liouville's Theorem
- Report rights infringement
- published: 10 Dec 2015
- views: 533

Simple proof of Liouville's theorem
- Report rights infringement
- published: 02 Jun 2022
- views: 793

Hamiltonian Formalism (3a): Liouville's Theorem (in Persian)
- Report rights infringement
- published: 10 Dec 2015
- views: 437

Liouville's theorem (Hamiltonian) | Wikipedia audio article
- Report rights infringement
- published: 28 Dec 2018
- views: 105

Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics. It asserts that the phase-space distribution function is constant along the trajectories of the system — that is that the density of system points in the vicinity of a given system point traveling through phase-space is constant with time.
There are related mathematical results in symplectic topology and ergodic theory.
Liouville equations
The Liouville equation describes the time evolution of the phase space distribution function. Although the equation is usually referred to as the "Liouville equation", Josiah Willard Gibbs was the first to recognize the importance of this equation as the fundamental equation of statistical mechanics. It is referred to as the Liouville equation because its derivation for non-canonical systems utilises an identity first derived by Liouville in 1838.
Consider a Hamiltonian dynamical system with canonical coordinates  and conjugate momenta
and conjugate momenta  , where
, where  . Then the phase space distribution
. Then the phase space distribution  determines the probability
determines the probability  that the system will be found in the infinitesimal phase space volume
that the system will be found in the infinitesimal phase space volume 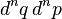 . The Liouville equation governs the evolution of
. The Liouville equation governs the evolution of  in time
in time  :
:
