- published: 15 Sep 2016
- views: 6294
Create your page here
Monday, 03 October 2016
-
remove the playlistEigenvalues
- remove the playlistEigenvalues
back to playlist
A visual understanding of eigenvectors, eigenvalues, and the usefulness of an eigenbasis.
This series comes to you from Khan Academy, watch the rest here: https://www.khanacademy.org/math/linear-algebra/eola-topic/eola/v/eola-preview
-------------
Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy
Help me by being a mathematical patron!
https://www.patreon.com/patrickjmt?ty=c
Part 2: Finding Eigenvalues and Eigenvectors: http://www.youtube.com/watch?v=IdsV0RaC9jM
Introduction to Eigenvalues and Eigenvectors - Part 1. Here I give the definition of an eigenvalue and an eigenvector. I then show a quick example illustrating the definition. Lastly, I show a quick proof that if we have an eigenvector then any multiple of that vector is also an eigenvector. Nothing crazy difficult here!
- published: 16 Aug 2012
- views: 447601
What eigenvectors and eigenvalues are and why they are interesting
Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-proof-of-formula-for-determining-eigenvalues?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Missed the previous lesson?
https://www.khanacademy.org/math/linear-algebra/alternate_bases/orthonormal_basis/v/linear-algebra-gram-schmidt-example-with-3-basis-vectors?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra implies two dimensional reasoning, however, the concepts covered in linear algebra provide the basis for multi-dimensional representations of mathematical reasoning. Matrices, vectors, vector spaces, transformations, eigenvectors/values all help us to visualize and understand multi dimensional concepts. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to KhanAcademy’s Linear Algebra channel: https://www.youtube.com/channel/UCGYSKl6e3HM0PP7QR35Crug?sub_confirmation=1
Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 13 Nov 2009
- views: 572962
Part 1 http://www.youtube.com/watch?v=G4N8vJpf7hM
This is the second video on Eigenvalues and EigenVectors.
Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example.
In this video I outline the general procedure for finding eigenvalues and eigenvectors for an n x n matrix and work an example using a 2 x 2 matrix.
- published: 27 Feb 2014
- views: 373412
Determining the eigenvalues of a 3x3 matrix
Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-eigenvectors-and-eigenspaces-for-a-3x3-matrix?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Missed the previous lesson?
https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-finding-eigenvectors-and-eigenspaces-example?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra implies two dimensional reasoning, however, the concepts covered in linear algebra provide the basis for multi-dimensional representations of mathematical reasoning. Matrices, vectors, vector spaces, transformations, eigenvectors/values all help us to visualize and understand multi dimensional concepts. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to KhanAcademy’s Linear Algebra channel: https://www.youtube.com/channel/UCGYSKl6e3HM0PP7QR35Crug?sub_confirmation=1
Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 14 Nov 2009
- views: 478932
Eigenvalues and eigenvectors play an important role in many signal processing applications. This example demonstrates the mechanics of computing the eigenvalues and eigenvectors of a specific 3x3 matrix. Eigenvalues are always the roots of the matrix characteristic equation, i.e. det(A-LI), while eigenvectors are found by finding the null space of the equation A-LI for each eigenvalue L.
- published: 23 Dec 2013
- views: 108322
Learn a physical example of application of eigenvalues and eigenvectors. For more videos and resources on this topic, please visit http://ma.mathforcollege.com/mainindex/10eigen/
- published: 01 Oct 2014
- views: 12108
Illustrate the process of finding eigenvalues and corresponding eigenvectors of a 3x3 matrix.
- published: 15 Sep 2014
- views: 107997
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler, Fall 2015
View the complete course: http://ocw.mit.edu/RES-18-009F15
Instructor: Gilbert Strang
The eigenvectors remain in the same direction when multiplied by the matrix. Subtracting an eigenvalue from the diagonal leaves a singular matrix: determinant zero. An n by n matrix has n eigenvalues.
License: Creative Commons BY-NC-SA
More information at http://ocw.mit.edu/terms
More courses at http://ocw.mit.edu
- published: 06 May 2016
- views: 1225
Eigenvalues and eigenvectors
In linear algebra, an eigenvector or characteristic vector of a square matrix is a vector that does not change its direction under the associated linear transformation. In other words—if v is a vector that is not zero, then it is an eigenvector of a square matrix A if Av is a scalar multiple of v. This condition could be written as the equation:
where λ is a scalar known as the eigenvalue or characteristic value associated with the eigenvector v. Geometrically, an eigenvector corresponding to a real, nonzero eigenvalue points in a direction that is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed.
There is a correspondence between n by n square matrices and linear transformations from an n-dimensional vector space to itself. For this reason, it is equivalent to define eigenvalues and eigenvectors using either the language of matrices or the language of linear transformations.
This page contains text from Wikipedia, the Free Encyclopedia -
https://wn.com/Eigenvalues_and_eigenvectors
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
This article is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License, which means that you can copy and modify it as long as the entire work (including additions) remains under this license.
- Loading...
-
17:16Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10
Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10
A visual understanding of eigenvectors, eigenvalues, and the usefulness of an eigenbasis. This series comes to you from Khan Academy, watch the rest here: https://www.khanacademy.org/math/linear-algebra/eola-topic/eola/v/eola-preview ------------- Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content. For free. For everyone. Forever. #YouCanLearnAnything Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy -
5:27Introduction to Eigenvalues and Eigenvectors - Part 1
Introduction to Eigenvalues and Eigenvectors - Part 1Introduction to Eigenvalues and Eigenvectors - Part 1
Help me by being a mathematical patron! https://www.patreon.com/patrickjmt?ty=c Part 2: Finding Eigenvalues and Eigenvectors: http://www.youtube.com/watch?v=IdsV0RaC9jM Introduction to Eigenvalues and Eigenvectors - Part 1. Here I give the definition of an eigenvalue and an eigenvector. I then show a quick example illustrating the definition. Lastly, I show a quick proof that if we have an eigenvector then any multiple of that vector is also an eigenvector. Nothing crazy difficult here! -
7:43Introduction to eigenvalues and eigenvectors | Linear Algebra | Khan Academy
Introduction to eigenvalues and eigenvectors | Linear Algebra | Khan AcademyIntroduction to eigenvalues and eigenvectors | Linear Algebra | Khan Academy
What eigenvectors and eigenvalues are and why they are interesting Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-proof-of-formula-for-determining-eigenvalues?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra Missed the previous lesson? https://www.khanacademy.org/math/linear-algebra/alternate_bases/orthonormal_basis/v/linear-algebra-gram-schmidt-example-with-3-basis-vectors?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra implies two dimensional reasoning, however, the concepts covered in linear algebra provide the basis for multi-dimensional representations of mathematical reasoning. Matrices, vectors, vector spaces, transformations, eigenvectors/values all help us to visualize and understand multi dimensional concepts. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra. About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content. For free. For everyone. Forever. #YouCanLearnAnything Subscribe to KhanAcademy’s Linear Algebra channel: https://www.youtube.com/channel/UCGYSKl6e3HM0PP7QR35Crug?sub_confirmation=1 Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy -
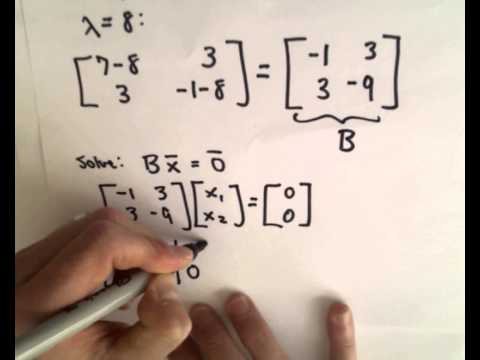13:41Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example
Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix ExampleFinding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example
Part 1 http://www.youtube.com/watch?v=G4N8vJpf7hM This is the second video on Eigenvalues and EigenVectors. Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example. In this video I outline the general procedure for finding eigenvalues and eigenvectors for an n x n matrix and work an example using a 2 x 2 matrix. -
5:16Eigenvalues - Sixty Symbols
Eigenvalues - Sixty Symbols -
14:08Eigenvalues of a 3x3 matrix | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
Eigenvalues of a 3x3 matrix | Alternate coordinate systems (bases) | Linear Algebra | Khan AcademyEigenvalues of a 3x3 matrix | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
Determining the eigenvalues of a 3x3 matrix Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-eigenvectors-and-eigenspaces-for-a-3x3-matrix?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra Missed the previous lesson? https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-finding-eigenvectors-and-eigenspaces-example?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra implies two dimensional reasoning, however, the concepts covered in linear algebra provide the basis for multi-dimensional representations of mathematical reasoning. Matrices, vectors, vector spaces, transformations, eigenvectors/values all help us to visualize and understand multi dimensional concepts. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra. About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content. For free. For everyone. Forever. #YouCanLearnAnything Subscribe to KhanAcademy’s Linear Algebra channel: https://www.youtube.com/channel/UCGYSKl6e3HM0PP7QR35Crug?sub_confirmation=1 Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy -
16:39Eigenvalue and Eigenvector Computations Example
Eigenvalue and Eigenvector Computations ExampleEigenvalue and Eigenvector Computations Example
Eigenvalues and eigenvectors play an important role in many signal processing applications. This example demonstrates the mechanics of computing the eigenvalues and eigenvectors of a specific 3x3 matrix. Eigenvalues are always the roots of the matrix characteristic equation, i.e. det(A-LI), while eigenvectors are found by finding the null space of the equation A-LI for each eigenvalue L. -
16:23A physical example of application of eigenvalues and eigenvectors
A physical example of application of eigenvalues and eigenvectorsA physical example of application of eigenvalues and eigenvectors
Learn a physical example of application of eigenvalues and eigenvectors. For more videos and resources on this topic, please visit http://ma.mathforcollege.com/mainindex/10eigen/ -
28:05Example of 3x3 Eigenvalues and Eigenvectors
Example of 3x3 Eigenvalues and EigenvectorsExample of 3x3 Eigenvalues and Eigenvectors
Illustrate the process of finding eigenvalues and corresponding eigenvectors of a 3x3 matrix. -
19:01Eigenvalues and Eigenvectors
Eigenvalues and EigenvectorsEigenvalues and Eigenvectors
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler, Fall 2015 View the complete course: http://ocw.mit.edu/RES-18-009F15 Instructor: Gilbert Strang The eigenvectors remain in the same direction when multiplied by the matrix. Subtracting an eigenvalue from the diagonal leaves a singular matrix: determinant zero. An n by n matrix has n eigenvalues. License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
-
Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10
A visual understanding of eigenvectors, eigenvalues, and the usefulness of an eigenbasis. This series comes to you from Khan Academy, watch the rest here: https://www.khanacademy.org/math/linear-algebra/eola-topic/eola/v/eola-preview ------------- Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to o...
published: 15 Sep 2016 -
Introduction to Eigenvalues and Eigenvectors - Part 1
Help me by being a mathematical patron! https://www.patreon.com/patrickjmt?ty=c Part 2: Finding Eigenvalues and Eigenvectors: http://www.youtube.com/watch?v=IdsV0RaC9jM Introduction to Eigenvalues and Eigenvectors - Part 1. Here I give the definition of an eigenvalue and an eigenvector. I then show a quick example illustrating the definition. Lastly, I show a quick proof that if we have an eigenvector then any multiple of that vector is also an eigenvector. Nothing crazy difficult here!
published: 16 Aug 2012 -
Introduction to eigenvalues and eigenvectors | Linear Algebra | Khan Academy
What eigenvectors and eigenvalues are and why they are interesting Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-proof-of-formula-for-determining-eigenvalues?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra Missed the previous lesson? https://www.khanacademy.org/math/linear-algebra/alternate_bases/orthonormal_basis/v/linear-algebra-gram-schmidt-example-with-3-basis-vectors?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more...
published: 13 Nov 2009 -
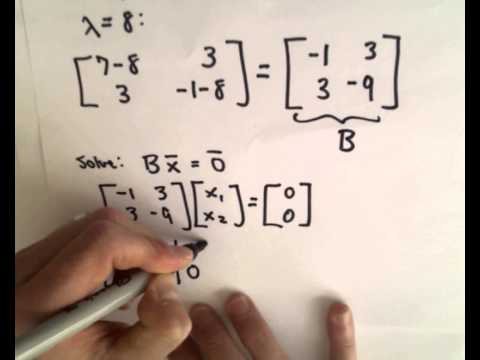
Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example
Part 1 http://www.youtube.com/watch?v=G4N8vJpf7hM This is the second video on Eigenvalues and EigenVectors. Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example. In this video I outline the general procedure for finding eigenvalues and eigenvectors for an n x n matrix and work an example using a 2 x 2 matrix.
published: 27 Feb 2014 -
-
Eigenvalues of a 3x3 matrix | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
Determining the eigenvalues of a 3x3 matrix Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-eigenvectors-and-eigenspaces-for-a-3x3-matrix?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra Missed the previous lesson? https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-finding-eigenvectors-and-eigenspaces-example?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra imp...
published: 14 Nov 2009 -
Eigenvalue and Eigenvector Computations Example
Eigenvalues and eigenvectors play an important role in many signal processing applications. This example demonstrates the mechanics of computing the eigenvalues and eigenvectors of a specific 3x3 matrix. Eigenvalues are always the roots of the matrix characteristic equation, i.e. det(A-LI), while eigenvectors are found by finding the null space of the equation A-LI for each eigenvalue L.
published: 23 Dec 2013 -
A physical example of application of eigenvalues and eigenvectors
Learn a physical example of application of eigenvalues and eigenvectors. For more videos and resources on this topic, please visit http://ma.mathforcollege.com/mainindex/10eigen/
published: 01 Oct 2014 -
Example of 3x3 Eigenvalues and Eigenvectors
Illustrate the process of finding eigenvalues and corresponding eigenvectors of a 3x3 matrix.
published: 15 Sep 2014 -
Eigenvalues and Eigenvectors
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler, Fall 2015 View the complete course: http://ocw.mit.edu/RES-18-009F15 Instructor: Gilbert Strang The eigenvectors remain in the same direction when multiplied by the matrix. Subtracting an eigenvalue from the diagonal leaves a singular matrix: determinant zero. An n by n matrix has n eigenvalues. License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
published: 06 May 2016
Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10
- Order: Reorder
- Duration: 17:16
- Updated: 15 Sep 2016
- views: 6294
A visual understanding of eigenvectors, eigenvalues, and the usefulness of an eigenbasis.
This series comes to you from Khan Academy, watch the rest here: http...
A visual understanding of eigenvectors, eigenvalues, and the usefulness of an eigenbasis.
This series comes to you from Khan Academy, watch the rest here: https://www.khanacademy.org/math/linear-algebra/eola-topic/eola/v/eola-preview
-------------
Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy
wn.com/Eigenvectors And Eigenvalues | Essence Of Linear Algebra, Chapter 10
A visual understanding of eigenvectors, eigenvalues, and the usefulness of an eigenbasis.
This series comes to you from Khan Academy, watch the rest here: https://www.khanacademy.org/math/linear-algebra/eola-topic/eola/v/eola-preview
-------------
Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 15 Sep 2016
- views: 6294
Introduction to Eigenvalues and Eigenvectors - Part 1
- Order: Reorder
- Duration: 5:27
- Updated: 16 Aug 2012
- views: 447601
Help me by being a mathematical patron!
https://www.patreon.com/patrickjmt?ty=c
Part 2: Finding Eigenvalues and Eigenvectors: http://www.youtube.com/watch?v=Id...
Help me by being a mathematical patron!
https://www.patreon.com/patrickjmt?ty=c
Part 2: Finding Eigenvalues and Eigenvectors: http://www.youtube.com/watch?v=IdsV0RaC9jM
Introduction to Eigenvalues and Eigenvectors - Part 1. Here I give the definition of an eigenvalue and an eigenvector. I then show a quick example illustrating the definition. Lastly, I show a quick proof that if we have an eigenvector then any multiple of that vector is also an eigenvector. Nothing crazy difficult here!
wn.com/Introduction To Eigenvalues And Eigenvectors Part 1
Help me by being a mathematical patron!
https://www.patreon.com/patrickjmt?ty=c
Part 2: Finding Eigenvalues and Eigenvectors: http://www.youtube.com/watch?v=IdsV0RaC9jM
Introduction to Eigenvalues and Eigenvectors - Part 1. Here I give the definition of an eigenvalue and an eigenvector. I then show a quick example illustrating the definition. Lastly, I show a quick proof that if we have an eigenvector then any multiple of that vector is also an eigenvector. Nothing crazy difficult here!
- published: 16 Aug 2012
- views: 447601
Introduction to eigenvalues and eigenvectors | Linear Algebra | Khan Academy
- Order: Reorder
- Duration: 7:43
- Updated: 13 Nov 2009
- views: 572962
What eigenvectors and eigenvalues are and why they are interesting
Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen...
What eigenvectors and eigenvalues are and why they are interesting
Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-proof-of-formula-for-determining-eigenvalues?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Missed the previous lesson?
https://www.khanacademy.org/math/linear-algebra/alternate_bases/orthonormal_basis/v/linear-algebra-gram-schmidt-example-with-3-basis-vectors?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra implies two dimensional reasoning, however, the concepts covered in linear algebra provide the basis for multi-dimensional representations of mathematical reasoning. Matrices, vectors, vector spaces, transformations, eigenvectors/values all help us to visualize and understand multi dimensional concepts. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to KhanAcademy’s Linear Algebra channel: https://www.youtube.com/channel/UCGYSKl6e3HM0PP7QR35Crug?sub_confirmation=1
Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy
wn.com/Introduction To Eigenvalues And Eigenvectors | Linear Algebra | Khan Academy
What eigenvectors and eigenvalues are and why they are interesting
Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-proof-of-formula-for-determining-eigenvalues?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Missed the previous lesson?
https://www.khanacademy.org/math/linear-algebra/alternate_bases/orthonormal_basis/v/linear-algebra-gram-schmidt-example-with-3-basis-vectors?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra implies two dimensional reasoning, however, the concepts covered in linear algebra provide the basis for multi-dimensional representations of mathematical reasoning. Matrices, vectors, vector spaces, transformations, eigenvectors/values all help us to visualize and understand multi dimensional concepts. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to KhanAcademy’s Linear Algebra channel: https://www.youtube.com/channel/UCGYSKl6e3HM0PP7QR35Crug?sub_confirmation=1
Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 13 Nov 2009
- views: 572962
Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example
- Order: Reorder
- Duration: 13:41
- Updated: 27 Feb 2014
- views: 373412
Part 1 http://www.youtube.com/watch?v=G4N8vJpf7hM
This is the second video on Eigenvalues and EigenVectors.
Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix ...
Part 1 http://www.youtube.com/watch?v=G4N8vJpf7hM
This is the second video on Eigenvalues and EigenVectors.
Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example.
In this video I outline the general procedure for finding eigenvalues and eigenvectors for an n x n matrix and work an example using a 2 x 2 matrix.
wn.com/Finding Eigenvalues And Eigenvectors 2 X 2 Matrix Example
Part 1 http://www.youtube.com/watch?v=G4N8vJpf7hM
This is the second video on Eigenvalues and EigenVectors.
Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example.
In this video I outline the general procedure for finding eigenvalues and eigenvectors for an n x n matrix and work an example using a 2 x 2 matrix.
- published: 27 Feb 2014
- views: 373412
Eigenvalues - Sixty Symbols
- Order: Reorder
- Duration: 5:16
- Updated: 14 Apr 2009
- views: 167406
From designing Google to building a bridge, eignevalues are important numbers... so important that Seamus Garvey has a fleet of computers devoted to them. More ...
From designing Google to building a bridge, eignevalues are important numbers... so important that Seamus Garvey has a fleet of computers devoted to them. More symbols at http://www.sixtysymbols.com/
wn.com/Eigenvalues Sixty Symbols
Eigenvalues of a 3x3 matrix | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
- Order: Reorder
- Duration: 14:08
- Updated: 14 Nov 2009
- views: 478932
Determining the eigenvalues of a 3x3 matrix
Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-al...
Determining the eigenvalues of a 3x3 matrix
Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-eigenvectors-and-eigenspaces-for-a-3x3-matrix?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Missed the previous lesson?
https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-finding-eigenvectors-and-eigenspaces-example?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra implies two dimensional reasoning, however, the concepts covered in linear algebra provide the basis for multi-dimensional representations of mathematical reasoning. Matrices, vectors, vector spaces, transformations, eigenvectors/values all help us to visualize and understand multi dimensional concepts. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to KhanAcademy’s Linear Algebra channel: https://www.youtube.com/channel/UCGYSKl6e3HM0PP7QR35Crug?sub_confirmation=1
Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy
wn.com/Eigenvalues Of A 3X3 Matrix | Alternate Coordinate Systems (Bases) | Linear Algebra | Khan Academy
Determining the eigenvalues of a 3x3 matrix
Watch the next lesson: https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-eigenvectors-and-eigenspaces-for-a-3x3-matrix?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Missed the previous lesson?
https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-finding-eigenvectors-and-eigenspaces-example?utm_source=YT&utm;_medium=Desc&utm;_campaign=LinearAlgebra
Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra implies two dimensional reasoning, however, the concepts covered in linear algebra provide the basis for multi-dimensional representations of mathematical reasoning. Matrices, vectors, vector spaces, transformations, eigenvectors/values all help us to visualize and understand multi dimensional concepts. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Subscribe to KhanAcademy’s Linear Algebra channel: https://www.youtube.com/channel/UCGYSKl6e3HM0PP7QR35Crug?sub_confirmation=1
Subscribe to KhanAcademy: https://www.youtube.com/subscription_center?add_user=khanacademy
- published: 14 Nov 2009
- views: 478932
Eigenvalue and Eigenvector Computations Example
- Order: Reorder
- Duration: 16:39
- Updated: 23 Dec 2013
- views: 108322
Eigenvalues and eigenvectors play an important role in many signal processing applications. This example demonstrates the mechanics of computing the eigenvalue...
Eigenvalues and eigenvectors play an important role in many signal processing applications. This example demonstrates the mechanics of computing the eigenvalues and eigenvectors of a specific 3x3 matrix. Eigenvalues are always the roots of the matrix characteristic equation, i.e. det(A-LI), while eigenvectors are found by finding the null space of the equation A-LI for each eigenvalue L.
wn.com/Eigenvalue And Eigenvector Computations Example
Eigenvalues and eigenvectors play an important role in many signal processing applications. This example demonstrates the mechanics of computing the eigenvalues and eigenvectors of a specific 3x3 matrix. Eigenvalues are always the roots of the matrix characteristic equation, i.e. det(A-LI), while eigenvectors are found by finding the null space of the equation A-LI for each eigenvalue L.
- published: 23 Dec 2013
- views: 108322
A physical example of application of eigenvalues and eigenvectors
- Order: Reorder
- Duration: 16:23
- Updated: 01 Oct 2014
- views: 12108
Learn a physical example of application of eigenvalues and eigenvectors. For more videos and resources on this topic, please visit http://ma.mathforcollege.com/...
Learn a physical example of application of eigenvalues and eigenvectors. For more videos and resources on this topic, please visit http://ma.mathforcollege.com/mainindex/10eigen/
wn.com/A Physical Example Of Application Of Eigenvalues And Eigenvectors
Learn a physical example of application of eigenvalues and eigenvectors. For more videos and resources on this topic, please visit http://ma.mathforcollege.com/mainindex/10eigen/
- published: 01 Oct 2014
- views: 12108
Example of 3x3 Eigenvalues and Eigenvectors
- Order: Reorder
- Duration: 28:05
- Updated: 15 Sep 2014
- views: 107997
Illustrate the process of finding eigenvalues and corresponding eigenvectors of a 3x3 matrix.
Illustrate the process of finding eigenvalues and corresponding eigenvectors of a 3x3 matrix.
wn.com/Example Of 3X3 Eigenvalues And Eigenvectors
Illustrate the process of finding eigenvalues and corresponding eigenvectors of a 3x3 matrix.
- published: 15 Sep 2014
- views: 107997
Eigenvalues and Eigenvectors
- Order: Reorder
- Duration: 19:01
- Updated: 06 May 2016
- views: 1225
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler, Fall 2015
View the complete course: http://ocw.mit.edu/RES-18-009F15
...
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler, Fall 2015
View the complete course: http://ocw.mit.edu/RES-18-009F15
Instructor: Gilbert Strang
The eigenvectors remain in the same direction when multiplied by the matrix. Subtracting an eigenvalue from the diagonal leaves a singular matrix: determinant zero. An n by n matrix has n eigenvalues.
License: Creative Commons BY-NC-SA
More information at http://ocw.mit.edu/terms
More courses at http://ocw.mit.edu
wn.com/Eigenvalues And Eigenvectors
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler, Fall 2015
View the complete course: http://ocw.mit.edu/RES-18-009F15
Instructor: Gilbert Strang
The eigenvectors remain in the same direction when multiplied by the matrix. Subtracting an eigenvalue from the diagonal leaves a singular matrix: determinant zero. An n by n matrix has n eigenvalues.
License: Creative Commons BY-NC-SA
More information at http://ocw.mit.edu/terms
More courses at http://ocw.mit.edu
- published: 06 May 2016
- views: 1225
back
- Playlist
- Chat
back
- Playlist
- Chat
17:16
Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10
A visual understanding of eigenvectors, eigenvalues, and the usefulness of an eigenbasis.
...
published: 15 Sep 2016
Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10
Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10
- Report rights infringement
- published: 15 Sep 2016
- views: 6294
5:27
Introduction to Eigenvalues and Eigenvectors - Part 1
Help me by being a mathematical patron!
https://www.patreon.com/patrickjmt?ty=c
Part 2: F...
published: 16 Aug 2012
Introduction to Eigenvalues and Eigenvectors - Part 1
Introduction to Eigenvalues and Eigenvectors - Part 1
- Report rights infringement
- published: 16 Aug 2012
- views: 447601
7:43
Introduction to eigenvalues and eigenvectors | Linear Algebra | Khan Academy
What eigenvectors and eigenvalues are and why they are interesting
Watch the next lesson:...
published: 13 Nov 2009
Introduction to eigenvalues and eigenvectors | Linear Algebra | Khan Academy
Introduction to eigenvalues and eigenvectors | Linear Algebra | Khan Academy
- Report rights infringement
- published: 13 Nov 2009
- views: 572962
13:41
Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example
Part 1 http://www.youtube.com/watch?v=G4N8vJpf7hM
This is the second video on Eigenvalues ...
published: 27 Feb 2014
Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example
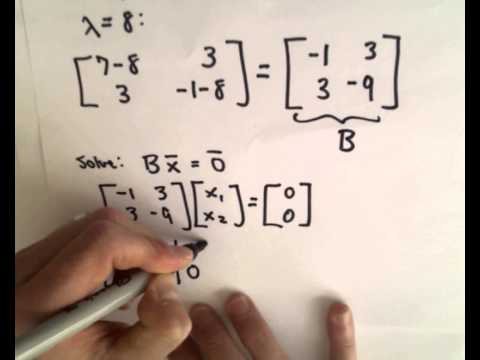
Finding Eigenvalues and Eigenvectors : 2 x 2 Matrix Example
- Report rights infringement
- published: 27 Feb 2014
- views: 373412
5:16
Eigenvalues - Sixty Symbols
From designing Google to building a bridge, eignevalues are important numbers... so import...
published: 14 Apr 2009
Eigenvalues - Sixty Symbols
Eigenvalues - Sixty Symbols
- Report rights infringement
- published: 14 Apr 2009
- views: 167406
14:08
Eigenvalues of a 3x3 matrix | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
Determining the eigenvalues of a 3x3 matrix
Watch the next lesson: https://www.khanacadem...
published: 14 Nov 2009
Eigenvalues of a 3x3 matrix | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
Eigenvalues of a 3x3 matrix | Alternate coordinate systems (bases) | Linear Algebra | Khan Academy
- Report rights infringement
- published: 14 Nov 2009
- views: 478932
16:39
Eigenvalue and Eigenvector Computations Example
Eigenvalues and eigenvectors play an important role in many signal processing applications...
published: 23 Dec 2013
Eigenvalue and Eigenvector Computations Example
Eigenvalue and Eigenvector Computations Example
- Report rights infringement
- published: 23 Dec 2013
- views: 108322
16:23
A physical example of application of eigenvalues and eigenvectors
Learn a physical example of application of eigenvalues and eigenvectors. For more videos a...
published: 01 Oct 2014
A physical example of application of eigenvalues and eigenvectors
A physical example of application of eigenvalues and eigenvectors
- Report rights infringement
- published: 01 Oct 2014
- views: 12108
28:05
Example of 3x3 Eigenvalues and Eigenvectors
Illustrate the process of finding eigenvalues and corresponding eigenvectors of a 3x3 matr...
published: 15 Sep 2014
Example of 3x3 Eigenvalues and Eigenvectors
Example of 3x3 Eigenvalues and Eigenvectors
- Report rights infringement
- published: 15 Sep 2014
- views: 107997
19:01
Eigenvalues and Eigenvectors
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler,...
published: 06 May 2016
Eigenvalues and Eigenvectors
Eigenvalues and Eigenvectors
- Report rights infringement
- published: 06 May 2016
- views: 1225
Eigenvectors and eigenvalues | Essence of linear a...
Introduction to Eigenvalues and Eigenvectors - Par...
Introduction to eigenvalues and eigenvectors | Lin...
Finding Eigenvalues and Eigenvectors : 2 x 2 Matri...
Eigenvalues - Sixty Symbols...
Eigenvalues of a 3x3 matrix | Alternate coordinate...
Eigenvalue and Eigenvector Computations Example...
A physical example of application of eigenvalues a...
Example of 3x3 Eigenvalues and Eigenvectors...
Eigenvalues and Eigenvectors...
photo: AP / Artyom Korotayev
Russia-Baiting and Risks of Nuclear War
Edit Antiwar 03 Oct 2016
As U.S. and Russian officials trade barbed threats and as diplomacy on Syria is “on the verge” of extinction, it is tempting to view the ongoing propaganda exchange over who shot down Malaysia Airlines Flight 17 in July 2014 as a sideshow ... Adult input is sorely needed. There are advantages to having some hands-on experience, and having watched how propaganda wars can easily escalate to military confrontation. In a Sept ... Goodman wrote....
photo: White House / Pete Souza
Why Obama Vetoed 9/11 Victims Bill in Support of Saudi Arabia and Atrocities
Edit WorldNews.com 03 Oct 2016
Article by WN.com correspondent Dallas Darling There is no doubt that the Saudi government supported the 9/11 hijackers. To be sure, and in speaking to “IBT Times,” ex-Senator Bob Graham who chaired the 9/11 Commission said. “The Saudi government without question was supporting the hijackers who lived in San Diego ... Obama and Saudi officials were in a state of outrage. U.S., Saudi, and Pakistan Connection to Remake Muslim World Mr....
photo: AP / John Locher
Trump running out of time as controversies pile up
Edit CNN 03 Oct 2016
Washington (CNN)Donald Trump's tax controversy and his self-destructive lack of discipline threaten to drain the Republican nominee of something he can't afford. time. With 36 days remaining before Election Day, the real estate mogul's campaign is consumed with the fallout from a New York Times story published over the weekend that found Trump reported a $916 million loss in 1995 ... Read More. Photos. Donald Trump's empire. Photos ... Sens ... ....
photo: WN / Bojana Ranic
Pakistan faced Iran firepower in Balochistan
Edit The Times of India 03 Oct 2016
NEW DELHI. The day India carried out surgical strikes across the Line of Control, Iranian Border Guards attacked Pakistan’s restive Balochistan region, sparking speculation whether it was a coordinated Indo-Iranian move amid warming ties. It has been learnt that Iranian forces fired three mortars into Balochistan area of Pakistan, taking the Pakistani Army by surprise ... Stay updated on the go with Times of India News App ... RELATED....
photo: NASA / ESA, M. Postman (STScI), and the CLASH Team
The 400-year-old quest for extraterrestrial life
Edit The National 03 Oct 2016
It is, perhaps, a telling observation that the two tools that first gave human beings the ability to explore the world about them in scientific detail, at both the universal and microscopic level, were invented at about the same time ... History credits his out-patented rival Zacharias Janssen, who was from the same town and is also believed to have been working on a telescope, with the invention of the microscope instead....
« back to news headlines
Thomas Pynchon changed my life...
Edit The Hindu 17 Sep 2016
I have always been an average kind of reader, like most normal people I know. I would usually read only when I was in between things. You know, like when I was on a flight and there was no Internet access. Or when I reached a restaurant 15 minutes early and my phone battery was low ... I used to read then ... Flipped on its head ... Right now, I can remember Pig Bodine, Eigenvalue, Stencil, Vera, and Evan (don’t ask me their genders, please)....
Stanford Professor Emeritus Joseph Keller, applied mathematician, dies at 93 (Stanford University)
Edit Public Technologies 08 Sep 2016
(Source. Stanford University) ... 7 at his home in Palo Alto, California. He was 93 ... For example, he used the method to describe eigenvalue spectra in quantum mechanics, to develop optimal strategies for runners in a race, to study the propagation of nerve pulses, to model the development of the visual system in mammals such as kittens, and to understand the locomotion of worms and how it differs from that of snakes ... Math runs in the family....
Recent trends in the analysis of spectral problems and applications (Politecnico di Torino)
Edit Public Technologies 01 Sep 2016
(Source. Politecnico di Torino). Categoria. Seminari e Convegni. Stato. Corrente. Politecnico di Torino, Aula Buzano, DISMA. AIMS AND SCOPES ... The mathematical discussion focuses mainly on recent contributions to the study of eigenvalues of differential operators and related shape optimization problems, Hamiltonian dispersive equations on graphs, and spectral properties of partial differential equations in perturbed waveguides ... SPEAKERS....
And They’re Off! Students Start First Day of Classes (Bowdoin College)
Edit Public Technologies 01 Sep 2016
(Source. Bowdoin College). The campus was busy Wednesday morning with students rushing across the Quad to attend their first class meetings. We caught up with a few of them to ask how their classes went ... PHIL 2111. Ancient Philosophy, with Associate Professor of Philosophy Sarah Conly ... JPN 2203 ... Topics include vectors, matrices, vector spaces, inner product spaces, linear transformations, eigenvalues and eigenvectors, and quadratic forms....
Lifetime of Numbers: Q&A; with Barry Simon (California Institute of Technology)
Edit Public Technologies 11 Aug 2016
The Notices article lists a number of accomplishments and I hesitate to single out only a few, but I'd mention my work on eigenvalue perturbation theory; the work with Francesco Guerra [University of Rome] and Lon Rosen [University of British Columbia] using statistical mechanical methods in Euclidean Quantum Field Theory; my work with Elliott Lieb ......
Laureation address: Professor Peter Sarnak (University of St Andrews)
Edit Public Technologies 24 Jun 2016
In a number of papers with Nick Katz, Ze'ev Rudnick and other co-authors, Sarnak worked on the mysterious relationship between the distribution of the zeros of various (highly non-random) number-theoretically defined functions, and that of the eigenvalues of random matrices - this relationship was first noted (experimentally) by Montgomery and ......
A new trick for controlling emission direction in microlasers (Washington University in Saint Louis)
Edit Public Technologies 17 Jun 2016
(Source. Washington University in Saint Louis). Researchers at Washington University in St. Louis have found a way to give photons, or light packets, their marching orders ... Lasing alone is a multibillion-dollar industry with thousands of applications from communication to medicine to hair removal ... & Florence G ... An exceptional point arises in physical fields when two complex eigenvalues and their eigenvectors coalesce, or become the same....
Erwin Schrodinger - Biographical Profile
Edit About.com 21 Feb 2016
Erwin Schrodinger was one of the key figures in the early development of quantum mechanics in the first half of the twentieth century.Biographical Information. Birthdate. August 12, 1887. Birthplace. Vienna, Austria. Death. January 4, 1961Spelling of Name ... Quantum Physics Achievements ... In this 1926 paper, he demonstrated that his equation yielded correct energy eigenvalues for a hydrogen-like atom ... Muller in the 1920's ... ....
Big Data Algorithms That Make Us Think (World Wide Technology Inc)
Edit Public Technologies 14 Dec 2015
(Source. World Wide Technology Inc). What big data analytics has to teach us about ourselves ... In a sense, the weight matrix of the synaptic connections can be interpreted as an eigenvalue decomposition problem in linear algebra, where all the eigenvalues have value 1 (identity), and the original matrix is decomposed into the tensor product of two sets of eigenvectors, one set to the left, and another transposed set to the right ... (noodl....
Dissertation: 18 Dec 2015 Spectral Analysis and Quantum Chaos in Two-Dimensional Nanostructures (Luukko) (University of ...
Edit Public Technologies 11 Dec 2015
This thesis describes a study into the eigenvalues and eigenstates of 2D quantum systems ... The study of quantum chaos by statistical properties of eigenvalues requires a way to solve the eigenvalue spectrum of a quantum system up to highly excited states ... The next step in the eigenvalue analysis is to remove the trivial part of the spectrum in a process known as unfolding....
Väitös: 18.12.15. Kvanttimekaniikassa kaaos näyttäytyy selkeinä, sovellettavina sormenjälkinä (Luukko) (University of Jyväskylä)
Edit Public Technologies 11 Dec 2015
This thesis describes a study into the eigenvalues and eigenstates of 2D quantum systems ... The study of quantum chaos by statistical properties of eigenvalues requires a way to solve the eigenvalue spectrum of a quantum system up to highly excited states ... The next step in the eigenvalue analysis is to remove the trivial part of the spectrum in a process known as unfolding....
Improved tools for structured matrix computations (Umeå universitet)
Edit Public Technologies 08 Dec 2015
(Source. Umeå universitet) Improved tools for structured matrix computations. [2015-12-08] To design and analyze a model of a mechanical system such as an electrical network or a chemical reaction process is often a complex problem that requires high-quality mathematical theories and computational tools ... A matrix pencil, in turn, consists of a pair of matrices and relates to the so-called generalized eigenvalue problem ... Text ... Telephone....
Biometrics and digital forensics: Cyber security connections
Edit Deccan Herald 02 Dec 2015
We use biometrics to identify criminals, or to exonerate those falsely accused. Traditionally, we have relied upon the unique pattern of fingerprints ... “Eigenface” is a term derived from “eigenvalues” and “eigenvectors,” which exist in pairs and refer to the “vectors” or directions of values that provide the largest “variance” or difference in a set of data points....
- 1
- 2
- 3
- 4
- 5
- Next page »
