Fracture mechanics
| Continuum mechanics |
|---|
 |
|
|
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.
In modern materials science, fracture mechanics is an important tool in improving the mechanical performance of materials and components. It applies the physics of stress and strain, in particular the theories of elasticity and plasticity, to the microscopic crystallographic defects found in real materials in order to predict the macroscopic mechanical failure of bodies. Fractography is widely used with fracture mechanics to understand the causes of failures and also verify the theoretical failure predictions with real life failures. The prediction of crack growth is at the heart of the damage tolerance discipline.
Contents |
[edit] Linear elastic fracture mechanics
[edit] Griffith's criterion
Fracture mechanics was developed during World War I by English aeronautical engineer, A. A. Griffith, to explain the failure of brittle materials.[1] Griffith's work was motivated by two contradictory facts:
- The stress needed to fracture bulk glass is around 100 MPa (15,000 psi).
- The theoretical stress needed for breaking atomic bonds is approximately 10,000 MPa (1,500,000 psi).
A theory was needed to reconcile these conflicting observations. Also, experiments on glass fibers that Griffith himself conducted suggested that the fracture stress increases as the fiber diameter decreases. Hence the uniaxial tensile strength, which had been used extensively to predict material failure before Griffith, could not be a specimen-independent material property. Griffith suggested that the low fracture strength observed in experiments, as well as the size-dependence of strength, was due to the presence of microscopic flaws in the bulk material.
To verify the flaw hypothesis, Griffith introduced an artificial flaw in his experimental specimens. The artificial flaw was in the form of a surface crack which was much larger than other flaws in a specimen. The experiments showed that the product of the square root of the flaw length (a) and the stress at fracture (σf) was nearly constant, which is expressed by the equation:
An explanation of this relation in terms of linear elasticity theory is problematic. Linear elasticity theory predicts that stress (and hence the strain) at the tip of a sharp flaw in a linear elastic material is infinite. To avoid that problem, Griffith developed a thermodynamic approach to explain the relation that he observed.
The growth of a crack requires the creation of two new surfaces and hence an increase in the surface energy. Griffith found an expression for the constant C in terms of the surface energy of the crack by solving the elasticity problem of a finite crack in an elastic plate. Briefly, the approach was:
- Compute the potential energy stored in a perfect specimen under a uniaxial tensile load.
- Fix the boundary so that the applied load does no work and then introduce a crack into the specimen. The crack relaxes the stress and hence reduces the elastic energy near the crack faces. On the other hand, the crack increases the total surface energy of the specimen.
- Compute the change in the free energy (surface energy − elastic energy) as a function of the crack length. Failure occurs when the free energy attains a peak value at a critical crack length, beyond which the free energy decreases by increasing the crack length, i.e. by causing fracture. Using this procedure, Griffith found that
where E is the Young's modulus of the material and γ is the surface energy density of the material. Assuming E = 62 GPa and γ = 1 J/m2 gives excellent agreement of Griffith's predicted fracture stress with experimental results for glass.
[edit] Irwin's modification
Griffith's work was largely ignored by the engineering community until the early 1950s. The reasons for this appear to be (a) in the actual structural materials the level of energy needed to cause fracture is orders of magnitude higher than the corresponding surface energy, and (b) in structural materials there are always some inelastic deformations around the crack front that would make the assumption of linear elastic medium with infinite stresses at the crack tip highly unrealistic. [2]
Griffith's theory provides excellent agreement with experimental data for brittle materials such as glass. For ductile materials such as steel, though the relation  still holds, the surface energy (γ) predicted by Griffith's theory is usually unrealistically high. A group working under G. R. Irwin[3] at the U.S. Naval Research Laboratory (NRL) during World War II realized that plasticity must play a significant role in the fracture of ductile materials.
still holds, the surface energy (γ) predicted by Griffith's theory is usually unrealistically high. A group working under G. R. Irwin[3] at the U.S. Naval Research Laboratory (NRL) during World War II realized that plasticity must play a significant role in the fracture of ductile materials.
In ductile materials (and even in materials that appear to be brittle[4]), a plastic zone develops at the tip of the crack. As the applied load increases, the plastic zone increases in size until the crack grows and the material behind the crack tip unloads. The plastic loading and unloading cycle near the crack tip leads to the dissipation of energy as heat. Hence, a dissipative term has to be added to the energy balance relation devised by Griffith for brittle materials. In physical terms, additional energy is needed for crack growth in ductile materials when compared to brittle materials.
Irwin's strategy was to partition the energy into two parts:
- the stored elastic strain energy which is released as a crack grows. This is the thermodynamic driving force for fracture.
- the dissipated energy which includes plastic dissipation and the surface energy (and any other dissipative forces that may be at work). The dissipated energy provides the thermodynamic resistance to fracture. Then the total energy dissipated is
where γ is the surface energy and Gp is the plastic dissipation (and dissipation from other sources) per unit area of crack growth.
The modified version of Griffith's energy criterion can then be written as
For brittle materials such as glass, the surface energy term dominates and  . For ductile materials such as steel, the plastic dissipation term dominates and
. For ductile materials such as steel, the plastic dissipation term dominates and  . For polymers close to the glass transition temperature, we have intermediate values of
. For polymers close to the glass transition temperature, we have intermediate values of  .
.
[edit] Stress intensity factor
Another significant achievement of Irwin and his colleagues was to find a method of calculating the amount of energy available for fracture in terms of the asymptotic stress and displacement fields around a crack front in a linear elastic solid.[3] This asymptotic expression for the stress field around a crack tip is
where σij are the Cauchy stresses, r is the distance from the crack tip, θ is the angle with respect to the plane of the crack, and fij are functions that are independent of the crack geometry and loading conditions. Irwin called the quantity K the stress intensity factor. Since the quantity fij is dimensionless, the stress intensity factor can be expressed in units of 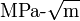 .
.
When a rigid line inclusion is considered, a similar asymptotic expression for the stress fields is obtained.
[edit] Strain energy release
Irwin was the first to observe that if the size of the plastic zone around a crack is small compared to the size of the crack, the energy required to grow the crack will not be critically dependent on the state of stress at the crack tip.[2] In other words, a purely elastic solution may be used to calculate the amount of energy available for fracture.
The energy release rate for crack growth or strain energy release rate may then be calculated as the change in elastic strain energy per unit area of crack growth, i.e.,
where U is the elastic energy of the system and a is the crack length. Either the load P or the displacement u can be kept fixed while evaluating the above expressions.
Irwin showed that for a mode I crack (opening mode) the strain energy release rate and the stress intensity factor are related by:
where E is the Young's modulus, ν is Poisson's ratio, and KI is the stress intensity factor in mode I. Irwin also showed that the strain energy release rate of a planar crack in a linear elastic body can be expressed in terms of the mode I, mode II (sliding mode), and mode III (tearing mode) stress intensity factors for the most general loading conditions.
Next, Irwin adopted the additional assumption that the size and shape of the energy dissipation zone remains approximately constant during brittle fracture. This assumption suggests that the energy needed to create a unit fracture surface is a constant that depends only on the material. This new material property was given the name fracture toughness and designated GIc. Today, it is the critical stress intensity factor KIc, found in the plain strain condition, which is accepted as the defining property in linear elastic fracture mechanics.
[edit] Limitations
But a problem arose for the NRL researchers because naval materials, e.g., ship-plate steel, are not perfectly elastic but undergo significant plastic deformation at the tip of a crack. One basic assumption in Irwin's linear elastic fracture mechanics is small scale yielding, the condition that the size of the plastic zone is small compared to the crack length. However, this assumption is quite restrictive for certain types of failure in structural steels though such steels can be prone to brittle fracture, which has led to a number of catastrophic failures.
Linear-elastic fracture mechanics is of limited practical use for structural steels for another more practical reason. Fracture toughness testing is very expensive and engineers believe that sufficient information for selection of steels can be obtained from the simpler and cheaper Charpy impact test.[citation needed]
[edit] Elastic–plastic fracture mechanics
Most engineering materials show some nonlinear elastic and inelastic behavior under operating conditions that involve large loads.[citation needed] In such materials the assumptions of linear elastic fracture mechanics may not hold, that is,
- the plastic zone at a crack tip may have a size of the same order of magnitude as the crack size
- the size and shape of the plastic zone may change as the applied load is increased and also as the crack length increases.
Therefore a more general theory of crack growth is needed for elastic-plastic materials that can account for:
- the local conditions for initial crack growth which include the nucleation, growth, and coalescence of voids or decohesion at a crack tip.
- a global energy balance criterion for further crack growth and unstable fracture.
[edit] CTOD
Historically, the first parameter for the determination of fracture toughness in the elasto-plastic was the CTOD Crack Tip Opening Displacement or "opening at the apex of the crack", indicated . This parameter was determined by Wells during the studies of structural steels which, due to the high toughness could not be characterized with the linear elastic fracture mechanics. He noted that, before it happened the fracture, the walls of the crack were leaving and that the crack tip, after fracture, acute to rounded off is due to plastic deformation. In addition, the rounding of the apex was more pronounced in steels with superior toughness. Wells demonstrate that under conditions of yield on a small scale is in connection with both K that with G.
[edit] R-curve
An early attempt in the direction of elastic-plastic fracture mechanics was Irwin's crack extension resistance curve, Crack growth resistance curve or R-curve. This curve acknowledges the fact that the resistance to fracture increases with growing crack size in elastic-plastic materials. The R-curve is a plot of the total energy dissipation rate as a function of the crack size and can be used to examine the processes of slow stable crack growth and unstable fracture. However, the R-curve was not widely used in applications until the early 1970s. The main reasons appear to be that the R-curve depends on the geometry of the specimen and the crack driving force may be difficult to calculate.[2]
[edit] J-integral
In the mid-1960s James R. Rice (then at Brown University) and G. P. Cherepanov independently developed a new toughness measure to describe the case where there is sufficient crack-tip deformation that the part no longer obeys the linear-elastic approximation. Rice's analysis, which assumes non-linear elastic (or monotonic deformation theory plastic) deformation ahead of the crack tip, is designated the J integral.[5] This analysis is limited to situations where plastic deformation at the crack tip does not extend to the furthest edge of the loaded part. It also demands that the assumed non-linear elastic behavior of the material is a reasonable approximation in shape and magnitude to the real material's load response. The elastic-plastic failure parameter is designated JIc and is conventionally converted to KIc using Equation (3.1) of the Appendix to this article. Also note that the J integral approach reduces to the Griffith theory for linear-elastic behavior.
The mathematical definition of J-integral is as follows:
, where
 is an arbitrary path clockwise around the apex of the crack,
is an arbitrary path clockwise around the apex of the crack,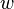 is the density of strain energy,
is the density of strain energy,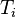 are the components of the vectors of traction,
are the components of the vectors of traction, the components of the displacement vectors and
the components of the displacement vectors and and an incremental length along the path
and an incremental length along the path  .
.
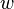 is also defined as:
is also defined as:
, Where
 and
and 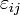 are the stress and strain tensors.
are the stress and strain tensors.
Hutchinson, Rice and Rosegreen subsequently showed that J characterizes the fields of stress and strain at the peak of the crack in nonlinear elastic materials. Hypothesized a material constitutive law similar to the relationship of Ramberg-Osgood:
, where
 and
and 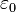 are respectively a stress and a strain of reference,
are respectively a stress and a strain of reference, is a dimensionless constant characteristic of the material and
is a dimensionless constant characteristic of the material and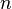 is the coefficient of work hardening.
is the coefficient of work hardening.
Apply the appropriate boundary conditions of the stress and strain fields are:
, where
 n are constants of integration and
n are constants of integration and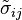 and
and 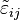 are dimensionless functions.
are dimensionless functions.
From these relations we see that , it tends to , so there is a singularity called HRR singularity . The J-integral defines the width of this singularity in the elastic-plastic, as well as K, the stress intensity factor, defines the singularity of linear elastic. It then describes in a complete way the fields of stress and strain at the peak of the crack in nonlinear elastic materials.
[edit] Cohesive zone models
When a significant region around a crack tip has undergone plastic deformation, other approaches can be used to determine the possibility of further crack extension and the direction of crack growth and branching. A simple technique that is easily incorporated into numerical calculations is the cohesive zone model method which is based on concepts proposed independently by Barenblatt[6] and Dugdale[7] in the early 1960s. The relationship between the Dugdale-Barenblatt models and Griffith's theory was first discussed by Willis in 1967.[8] The equivalence of the two approaches in the context of brittle fracture was shown by Rice in 1968.[5] Interest in cohesive zone modeling of fracture has been reignited since 2000 following the pioneering work on dynamic fracture by Xu and Needleman,[9] and Camacho and Ortiz.[10]
[edit] Cracktip constraint under large scale yielding
Under small-scale yielding conditions, a single parameter (e.g., K, J, or CTOD) characterizes cracktip conditions and can be used as a geometry-independent fracture criterion. Single-parameter fracture mechanics breaks down in the presence of excessive plasticity, and the fracture toughness depends on the size and geometry of the test specimen. The theories used for large scale yeilding is not very standerdised. The following theories/ approaches are commonly used amoung researchers in this field
[edit] Elastic T stress
[edit] J-Q Theory
[edit] Engineering applications
The following information is needed for a fracture mechanics prediction of failure:
- Applied load
- Residual stress
- Size and shape of the part
- Size, shape, location, and orientation of the crack
Usually not all of this information is available and conservative assumptions have to be made.
Occasionally post-mortem fracture-mechanics analyses are carried out. In the absence of an extreme overload, the causes are either insufficient toughness (KIc) or an excessively large crack that was not detected during routine inspection.
[edit] Short summary
Arising from the manufacturing process, interior and surface flaws are found in all metal structures. Not all such flaws are unstable under service conditions. Fracture mechanics is the analysis of flaws to discover those that are safe (that is, do not grow) and those that are liable to propagate as cracks and so cause failure of the flawed structure. Ensuring safe operation of structure despite these inherent flaws is achieved through damage tolerance analysis. Fracture mechanics as a subject for critical study has barely been around for a century and thus is relatively new. There is a high demand for engineers with fracture mechanics expertise—particularly in this day and age where engineering failure is considered 'shocking' amongst the general public.
[edit] Appendix: mathematical relations
[edit] Griffith's criterion
For the simple case of a thin rectangular plate with a crack perpendicular to the load Griffith’s theory becomes:
 (1.1)
(1.1)
where  is the strain energy release rate,
is the strain energy release rate, 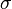 is the applied stress,
is the applied stress,  is half the crack length, and
is half the crack length, and  is the Young’s modulus. The strain energy release rate can otherwise be understood as: the rate at which energy is absorbed by growth of the crack.
is the Young’s modulus. The strain energy release rate can otherwise be understood as: the rate at which energy is absorbed by growth of the crack.
However, we also have that:
 (1.2)
(1.2)
If  ≥
≥  , this is the criterion for which the crack will begin to propagate.
, this is the criterion for which the crack will begin to propagate.
[edit] Irwin's modifications
Eventually a modification of Griffith’s solids theory emerged from this work; a term called stress intensity replaced strain energy release rate and a term called fracture toughness replaced surface weakness energy. Both of these terms are simply related to the energy terms that Griffith used:
 (2.1)
(2.1)
and
 (for plane stress) (2.2)
(for plane stress) (2.2)
 (for plane strain) (2.3)
(for plane strain) (2.3)
where KI is the stress intensity, Kc the fracture toughness, and  is Poisson’s ratio. It is important to recognize the fact that fracture parameter Kc has different values when measured under plane stress and plane strain
is Poisson’s ratio. It is important to recognize the fact that fracture parameter Kc has different values when measured under plane stress and plane strain
Fracture occurs when  . For the special case of plane strain deformation,
. For the special case of plane strain deformation,  becomes
becomes  and is considered a material property. The subscript I arises because of the different ways of loading a material to enable a crack to propagate. It refers to so-called "mode I" loading as opposed to mode II or III:
and is considered a material property. The subscript I arises because of the different ways of loading a material to enable a crack to propagate. It refers to so-called "mode I" loading as opposed to mode II or III:
There are three ways of applying a force to enable a crack to propagate:
- Mode I crack – Opening mode (a tensile stress normal to the plane of the crack)
- Mode II crack – Sliding mode (a shear stress acting parallel to the plane of the crack and perpendicular to the crack front)
- Mode III crack – Tearing mode (a shear stress acting parallel to the plane of the crack and parallel to the crack front)
We must note that the expression for  in equation 2.1 will be different for geometries other than the center-cracked infinite plate, as discussed in the article on the stress intensity factor. Consequently, it is necessary to introduce a dimensionless correction factor, Y, in order to characterize the geometry. We thus have:
in equation 2.1 will be different for geometries other than the center-cracked infinite plate, as discussed in the article on the stress intensity factor. Consequently, it is necessary to introduce a dimensionless correction factor, Y, in order to characterize the geometry. We thus have:
 (2.4)
(2.4)
where Y is a function of the crack length and width of sheet given by:
 (2.5)
(2.5)
for a sheet of finite width W containing a through-thickness crack of length 2a, or
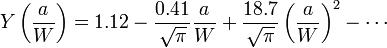 (2.6)
(2.6)
for a sheet of finite width W containing a through-thickness edge crack of length a
[edit] Elasticity and plasticity
Since engineers became accustomed to using KIc to characterise fracture toughness, a relation has been used to reduce JIc to it:
 where
where  for plane stress and
for plane stress and  for plane strain (3.1)
for plane strain (3.1)
The remainder of the mathematics employed in this approach is interesting, but is probably better summarised in external pages due to its complex nature.
APPLICATIONS OF FRACTURE MECHANICS.
Design process for a component is choosing appropriate geometry, material strength as per the loading conditions (either cyclic or constant loading), temperature of usage and structural analysis (Testing and FEM analysis) so that it doesn't fail under load. The methodologies followed in design criteria is traditional picking up the conventional materials based on standard data book and as per the loading conditions proportioning the geometry of the components on basis of analysis, this method is not applicable for some new innovation like usage of new material in design. Another method followed is that as per the loading conditions, static analysis is done for the structure as per the results the forces acting on each component, material strength and geometry is chosen. The material strength is chosen keeping in mind the factor of safety i.e., the ultimate stress (where it fails) is much higher than maximum stress in the component. The general assumptions in the design criteria lack of discontinuities , no defects or cracks in the material and even in the presence of discontinuities material is assumed to have sufficient ductility to yield locally so that redistribution of stress at discontinuities occur. And many investigation of failed components proved that crack growth was started because of discontinuities. Fracture mechanics follows the two design principles either fail-safe or safe-life. In fail safe even if a component fails the entire structure is not at risk (redundant member’s fails) or in safe life principle - throughout the life, no component of the structure fails. Fracture mechanics estimated maximum crack that a material can withstand before it fails through analysis taking into considerations of overall dimensions of the structure, stress value where crack ignition takes place, notch toughness value (ability of a material to absorb energy in the presence of crack for crack propagation), behavior of materials under the action of stresses by finding out stress intensity factor (K), fatigue crack growth and stress corrosion crack growth. As followed in basic solid mechanics analysis that stress in the component should be less than yielding stress same principle is applied i.e., stress intensity factor should be less that critical stress intensity factor. Major applications of fracture mechanics design are material selection, effect of defects, failure analysis and control/monitoring of components. Fracture analysis includes usage of mathematical models such as liner elastic fracture mechanics (LEFM), crack opening displacement (COD) and J Integral approaches by using Finite element analysis (FEM). The relationship used for estimating stress intensity factor is
K =c σ √a Where, k – Critical fracture toughness value
C – Constant that depends on crack and specimen dimensions. σ- Applied stress a – Flaw size Above relation is very general and as per the shape of the crack, relations available in standard data books or course books are to be used, any general crack can be approximated to standards used in writing the relations. For a material K value is dependent on stresses acting and flaw size. Flaw size decreases as the stress increases. So any design engineer can dictate the life of a component by choosing appropriate values of K, a and σ. And even there are other parameters that estimate the life of a component like working temperature, loading rate (Fatigue), residual stress and stress concentration. Higher the K value more is the resistance to crack growth so more stresses it can resist. Designers try to decrease the defects in the component because of casting or manufacturing processes by following good fabrication processes and inspection, and estimates notch-toughness values of materials using methods like charpy V-notch impact test, drop weight tests. In many investigations it was proved that material failed very much less that critical stress intensity factor because of defects in the material or micro cracks. Analysis proved that for any component there are two phases for crack development i.e., crack initiation and second phase crack growth until failure. Of which first phase covers a larger percentage of fatigue life and under very large high cycle loading conditions second phase is instantaneous.
The factor (k/ σ)² is used for estimating design of component because it estimates crack size, more the value better the resistance to the forces(Stress). But how large this factor has to be is decided by considering type of the structure, frequency of inspection, access to inspection, design life of the structure, consequences of failure, probability of over load, methods of fabrication, required quality, material cost in addition to the results obtained by fracture mechanics analysis.
[edit] See also
- AFGROW - Fracture mechanics and fatigue crack growth analysis software
- Fracture toughness
- Fatigue
- Peridynamics (a numerical method to solve fracture mechanics problems)
- Shock (mechanics)
- Strength of glass
- Strength of materials
- Stress corrosion cracking
- Stress intensity factor
- Strain energy release rate
- Structural fracture mechanics
- Concrete Fracture Analysis
[edit] References
[edit] Notes
- ^ Griffith, A. A. (1921), "The phenomena of rupture and flow in solids", Philosophical Transactions of the Royal Society of London, A 221: 163–198.
- ^ a b c E. Erdogan (2000) Fracture Mechanics, International Journal of Solids and Structures, 37, pp. 171–183.
- ^ a b Irwin G (1957), Analysis of stresses and strains near the end of a crack traversing a plate, Journal of Applied Mechanics 24, 361–364.
- ^ Orowan, E., 1948. Fracture and strength of solids. Reports on Progress in Physics XII, 185–232.
- ^ a b Rice, J. R. (1968), "A path independent integral and the approximate analysis of strain concentration by notches and cracks", Journal of Applied Mechanics 35: 379–386, Bibcode:1968JAM....35..379R, doi:10.1115/1.3601206.
- ^ Barenblatt, G. I. (1962), "The mathematical theory of equilibrium cracks in brittle fracture", Advances in applied mechanics 7: 55–129
- ^ Dugdale, D. S. (1960), "Yielding of steel sheets containing slits", Journal of the Mechanics and Physics of Solids 8 (2): 100–104
- ^ Willis, J. R. (1967), "A comparison of the fracture criteria of Griffith and Barenblatt", Journal of the Mechanics and Physics of Solids 15 (3): 151–162.
- ^ Xu, X.P. and Needleman, A. (1994), "Numerical simulations of fast crack growth in brittle solids", Journal of the Mechanics and Physics of Solids 42 (9): 1397–1434
- ^ Camacho, G. T. and Ortiz, M. (1996), "Computational modelling of impact damage in brittle materials", International Journal of Solids and Structures 33 (20-22): 2899–2938
[edit] Bibliography
- C. P. Buckley, "Material Failure", Lecture Notes (2005), University of Oxford.
- T. L. Anderson, "Fracture Mechanics: Fundamentals and Applications" (1995) CRC Press.
[edit] Further reading
- Davidge, R.W., Mechanical Behavior of Ceramics, Cambridge Solid State Science Series, (1979)
- Green, D., An Introduction to the Mechanical Properties of Ceramics, Cambridge Solid State Science Series, Eds. Clarke, D.R., Suresh, S., Ward, I.M. (1998)
- Lawn, B.R., Fracture of Brittle Solids, Cambridge Solid State Science Series, 2nd Edn. (1993)
- Farahmand, B., Bockrath, G., and Glassco, J. (1997) Fatigue and Fracture Mechanics of High-Risk Parts, Chapman & Hall.
- Chen, X., Mai, Y.-W., Fracture Mechanics of Electromagnetic Materials: Nonlinear Field Theory and Applications, Imperial College Press, (2012)
- Fracture mechanics fundamentals and applications by Anderson.
[edit] External links
- eFunda – Fracture Mechanics
- Fracture Mechanics by Prof. Alan Zehnder (from Cornell University)
- Fracture Mechanics for Engineers
- Nonlinear Fracture Mechanics Notes by Prof. John Hutchinson (from Harvard University)
- Notes on Fracture of Thin Films and Multilayers by Prof. John Hutchinson (from Harvard University)
- Fracture Mechanics by Prof. Piet Schreurs (from TU Eindhoven, Netherlands)
- Introduction to Fracture Mechanics by Dr. C. H. Wang (DSTO – Australia)
- Fracture mechanics course notes by Prof. Rui Huang (from Univ. of Texas at Austin)
- http://enterprise.astm.org/SUBSCRIPTION/DIGITAL_LIBRARY/MNL/PAGES/MNL10328M.htm
- http://www.keytometals.com/page.aspx?ID=CheckArticle&site=kts&NM=353

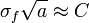
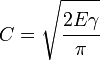




![G := \left[\cfrac{\partial U}{\partial a}\right]_P = -\left[\cfrac{\partial U}{\partial a}\right]_u](http://web.archive.org./web/20130425204801im_/http://upload.wikimedia.org/math/4/3/a/43a5d77d8f93cf0fcd75bec0d7067e3e.png)




 is an arbitrary path clockwise around the apex of the crack,
is an arbitrary path clockwise around the apex of the crack,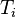 are the components of the vectors of traction,
are the components of the vectors of traction, the components of the displacement vectors and
the components of the displacement vectors and and an incremental length along the path
and an incremental length along the path 
 and
and 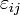 are the stress and strain tensors.
are the stress and strain tensors.
 and
and 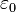 are respectively a stress and a strain of reference,
are respectively a stress and a strain of reference, is a dimensionless constant characteristic of the material and
is a dimensionless constant characteristic of the material and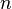 is the coefficient of work hardening.
is the coefficient of work hardening.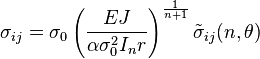

 n are constants of integration and
n are constants of integration and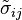 and
and 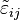 are dimensionless functions.
are dimensionless functions. (1.1)
(1.1) (1.2)
(1.2) (2.1)
(2.1) (for
(for  (for
(for 
 (2.4)
(2.4) (2.5)
(2.5)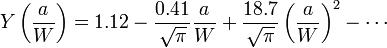 (2.6)
(2.6) where
where  for plane stress and
for plane stress and  for plane strain (3.1)
for plane strain (3.1)