- go to the top
- About WN
- Contact
- Feedback
- Privacy Policy
- © 2012 World News Inc., all Rights Reserved
- Loading...

-
Florian Cajori
Florian Cajori (February 28, 1859 in St Aignan (near Thusis), Graubünden, Switzerland—August 15, 1930, Berkeley, California) was one of the most celebrated historians of mathematics in his day.
http://wn.com/Florian_Cajori -
Lord Kelvin
http://wn.com/Lord_Kelvin -
Roger Cotes
Roger Cotes FRS (10 July 1682 — 5 June 1716) was an English mathematician, known for working closely with Isaac Newton by proofreading the second edition of his famous book, the Principia, before publication. He also invented the quadrature formulas known as Newton–Cotes formulas and first introduced what is known today as Euler's formula. He was the first Plumian Professor at Cambridge University from 1707 until his death.
http://wn.com/Roger_Cotes
-
Belfast
Belfast () is the capital of and the largest city in Northern Ireland. It is the seat of devolved government and legislative Northern Ireland Assembly. It is the largest urban area in Northern Ireland, the second-largest city in Ireland and the 15th-largest city in the United Kingdom. It is the main settlement in the province of Ulster. The city of Belfast has a population of 267,500 and lies at the heart of the Belfast urban area, which has a population of 483,418. The Belfast metropolitan area has a total population of 579,276. Belfast is also the 100th-largest urban zone in the EU. Belfast was granted city status in 1888.
http://wn.com/Belfast
- angle
- angular acceleration
- Angular frequency
- Angular mil
- angular velocity
- Arc (geometry)
- beam divergence
- Belfast
- calculus
- circle
- Degree (angle)
- Dimensionless number
- Euler's formula
- exponential function
- Florian Cajori
- Grad (angle)
- gun
- Harmonic analysis
- laser
- limit of a function
- Lord Kelvin
- mathematics
- MathWorld
- phase (waves)
- phase difference
- physics
- pi
- Polar coordinates
- pure number
- radius
- Roger Cotes
- SI derived unit
- SI prefix
- Sniper
- solid angle
- steradian
- subtended
- tau
- Taylor series
- Trigonometry
- turn (geometry)
- °
- θ
Radian, Vladimir Filmography
- Hogtown Blues (2004)
- Beyond Borders (2003)
- Spinning Boris (2003)
- The In-Laws (2003)
- Haven't We Met Before? (2002)
- The Sum of All Fears (2002)
- Aldrich Ames: Traitor Within (1998)
Radian, Béatrice Filmography
- Le retour des bidasses en folie (1983)
- Qu'est-ce qui fait craquer les filles... (1982)
- Comment draguer toutes les filles... (1981)
- L'associé (1979)

- Order: Reorder
- Duration: 9:55
- Published: 14 Aug 2007
- Uploaded: 29 Feb 2012
- Author: khanacademy

- Order: Reorder
- Duration: 9:11
- Published: 23 Jan 2009
- Uploaded: 23 Feb 2012
- Author: ExamSolutions
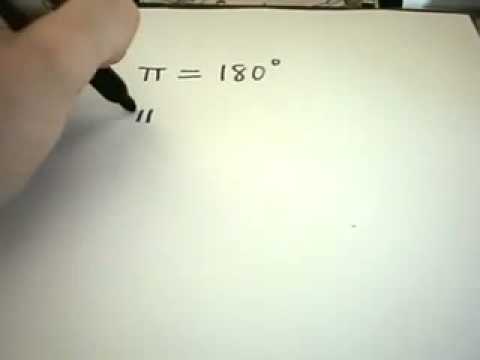
- Order: Reorder
- Duration: 11:59
- Published: 01 Dec 2008
- Uploaded: 28 Feb 2012
- Author: patrickJMT

- Order: Reorder
- Duration: 6:32
- Published: 03 Apr 2010
- Uploaded: 27 Feb 2012
- Author: joehandsome99

- Order: Reorder
- Duration: 4:23
- Published: 15 Dec 2010
- Uploaded: 24 Feb 2012
- Author: shaktimusic99

- Order: Reorder
- Duration: 8:19
- Published: 10 May 2007
- Uploaded: 28 Feb 2012
- Author: mathstutorbiz


- Order: Reorder
- Duration: 1:00
- Published: 08 Jun 2011
- Uploaded: 17 Feb 2012
- Author: MathDoctorMitchell

- Order: Reorder
- Duration: 3:19
- Published: 03 Oct 2009
- Uploaded: 28 Feb 2012
- Author: AussieJarred



- Order: Reorder
- Duration: 8:47
- Published: 12 Jun 2009
- Uploaded: 10 Feb 2012
- Author: loribee1989

- Order: Reorder
- Duration: 8:43
- Published: 14 Aug 2010
- Uploaded: 29 Feb 2012
- Author: asesoriasdematecom

- Order: Reorder
- Duration: 4:11
- Published: 23 Jan 2010
- Uploaded: 07 Feb 2012
- Author: ghostsonatasong


- Order: Reorder
- Duration: 5:19
- Published: 07 Oct 2009
- Uploaded: 28 Feb 2012
- Author: Mindbitesdotcom


- Order: Reorder
- Duration: 5:56
- Published: 08 Nov 2010
- Uploaded: 23 Feb 2012
- Author: patrickJMT


- Order: Reorder
- Duration: 5:24
- Published: 25 Feb 2010
- Uploaded: 06 Sep 2011
- Author: Babyssentials

- Order: Reorder
- Duration: 4:10
- Published: 21 May 2011
- Uploaded: 25 Aug 2011
- Author: randomtrixie


- Order: Reorder
- Duration: 5:17
- Published: 24 Apr 2011
- Uploaded: 10 Feb 2012
- Author: MothMessage
- A. Eagle
- angle
- angular acceleration
- Angular frequency
- Angular mil
- angular velocity
- Arc (geometry)
- beam divergence
- Belfast
- calculus
- circle
- Degree (angle)
- Dimensionless number
- Euler's formula
- exponential function
- Florian Cajori
- Grad (angle)
- gun
- Harmonic analysis
- laser
- limit of a function
- Lord Kelvin
- mathematics
- MathWorld
- phase (waves)
- phase difference
- physics
- pi
- Polar coordinates
- pure number
- radius
- Roger Cotes
- SI derived unit
- SI prefix
- Sniper
- solid angle
- steradian
- subtended
- tau
- Taylor series
- Trigonometry
- turn (geometry)
- °
- θ
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit. The SI unit of solid angle measurement is the steradian.
The radian is represented by the symbol "rad" or, more rarely, by the superscript c (for "circular measure"). For example, an angle of 1.2 radians would be written as "1.2 rad" or "1.2c" (the second symbol is often mistaken for a degree: "1.2°"). As the ratio of two lengths, the radian is a "pure number" that needs no unit symbol, and in mathematical writing the symbol "rad" is almost always omitted. In the absence of any symbol radians are assumed, and when degrees are meant the symbol ° is used.
Definition
Radian describes the plane angle subtended by a circular arc as the length of the arc divided by the radius of the arc. One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. More generally, the magnitude in radians of such a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, ''θ'' = ''s'' /''r'', where ''θ'' is the subtended angle in radians, ''s'' is arc length, and ''r'' is radius. Conversely, the length of the enclosed arc is equal to the radius multiplied by the magnitude of the angle in radians; that is, ''s'' = ''rθ''.It follows that the magnitude in radians of one complete revolution (360 degrees) is the length of the entire circumference divided by the radius, or 2π''r'' /''r'', or 2π. Thus 2π radians is equal to 360 degrees, meaning that one radian is equal to 180/π degrees.
History
The concept of radian measure, as opposed to the degree of an angle, should probably be credited to Roger Cotes in 1714. He had the radian in everything but name, and he recognized its naturalness as a unit of angular measure.The term ''radian'' first appeared in print on 5 June 1873, in examination questions set by James Thomson (brother of Lord Kelvin) at Queen's College, Belfast. He used the term as early as 1871, while in 1869, Thomas Muir, then of the University of St Andrews, vacillated between ''rad'', ''radial'' and ''radian''. In 1874, Muir adopted ''radian'' after a consultation with James Thomson.
Conversions
Conversion between radians and degrees
As stated, one radian is equal to 180/π degrees. Thus, to convert from radians to degrees, multiply by 180/π.:
For example: : : :
Conversely, to convert from degrees to radians, multiply by π/180.
:
For example:
:
Radians can be converted to turns by dividing the number of radians by 2π.
Radian to degree conversion derivation
We know that the length of circumference of a circle is given by , where is the radius of the circle.So, we can very well say that the following equivalent relation is true:
[Since a sweep is need to draw a full circle]
By definition of radian, we can formulate that a full circle represents:
:
:
Combining both the above relations we can say:
:
:
:
Conversion between radians and grads
radians are equal to one turn, which is 400g. So, to convert from radians to grads multiply by , and to convert from grads to radians multiply by . For example,: :
The table shows the conversion of some common angles.
{|class = wikitable ! Units !! colspan=8 | Values |- valign="top" |style="background:#f2f2f2" | Turns |style="width:3em; text-align:center" | 0 |style="width:3em; text-align:center" | |style="width:3em; text-align:center" | |style="width:3em; text-align:center" | |style="width:3em; text-align:center" | |style="width:3em; text-align:center" | |style="width:3em; text-align:center" | |style="width:3em; text-align:center" | |- valign="top" |style="background:#f2f2f2" | Degrees |style="width:3em; text-align:center" | 0° |style="width:3em; text-align:center" | 30° |style="width:3em; text-align:center" | 45° |style="width:3em; text-align:center" | 60° |style="width:3em; text-align:center" | 90° |style="width:3em; text-align:center" | 180° |style="width:3em; text-align:center" | 270° |style="width:3em; text-align:center" | 360° |- valign="top" |style="background:#f2f2f2" | Radians |style="text-align:center" | 0 |style="text-align:center" | |style="text-align:center" | |style="text-align:center" | |style="text-align:center" | |style="text-align:center" | |style="text-align:center" | |style="text-align:center" | 2 |- valign="top" |style="background:#f2f2f2" | Grads |style="text-align:center" | 0g |style="text-align:center" | |style="text-align:center" | 50g |style="text-align:center" | |style="text-align:center" | 100g |style="text-align:center" | 200g |style="text-align:center" | 300g |style="text-align:center" | 400g |}
Since a turn is often identified with the circle constant there is essentially no difference between measuring angles in turns and in radians.
Advantages of measuring in radians
In calculus and most other branches of mathematics beyond practical geometry, angles are universally measured in radians. This is because radians have a mathematical "naturalness" that leads to a more elegant formulation of a number of important results.
Most notably, results in analysis involving trigonometric functions are simple and elegant when the functions' arguments are expressed in radians. For example, the use of radians leads to the simple limit formula
:
which is the basis of many other identities in mathematics, including
: :
Because of these and other properties, the trigonometric functions appear in solutions to mathematical problems that are not obviously related to the functions' geometrical meanings (for example, the solutions to the differential equation , the evaluation of the integral , and so on). In all such cases it is found that the arguments to the functions are most naturally written in the form that corresponds, in geometrical contexts, to the radian measurement of angles.
The trigonometric functions also have simple and elegant series expansions when radians are used; for example, the following Taylor series for sin ''x'' :
:
If ''x'' were expressed in degrees then the series would contain messy factors involving powers of π/180: if ''x'' is the number of degrees, the number of radians is ''y'' = π''x'' /180, so
:
Mathematically important relationships between the sine and cosine functions and the exponential function (see, for example, Euler's formula) are, again, elegant when the functions' arguments are in radians and messy otherwise.
Dimensional analysis
Although the radian is a unit of measure, it is a dimensionless quantity. This can be seen from the definition given earlier: the angle subtended at the centre of a circle, measured in radians, is equal to the ratio of the length of the enclosed arc to the length of the circle's radius. Since the units of measurement cancel, this ratio is dimensionless.Another way to see the dimensionlessness of the radian is in the series representations of the trigonometric functions, such as the Taylor series for sin ''x'' mentioned earlier:
:
If ''x'' had units, then the sum would be meaningless: the linear term ''x'' cannot be added to (or have subtracted) the cubic term or the quintic term , etc. Therefore, ''x'' must be dimensionless.
Although polar and spherical coordinates use radians to describe coordinates in two and three dimensions, the unit is derived from the radius coordinate, so the angle measure is still dimensionless.
Use in physics
The radian is widely used in physics when angular measurements are required. For example, angular velocity is typically measured in radians per second (rad/s). One revolution per second is equal to 2π radians per second.Similarly, angular acceleration is often measured in radians per second per second (rad/s2).
For the purpose of dimensional analysis, the units are s−1 and s−2 respectively.
Likewise, the phase difference of two waves can also be measured in radians. For example, if the phase difference of two waves is (k·2π) radians, where k is an integer, they are considered in phase, whilst if the phase difference of two waves is (k·2π + π), where k is an integer, they are considered in antiphase.
Multiples of radian units
Metric prefixes have limited use with radians, and none in mathematics.An approximation of the milliradian (0.001 rad), known as the mil, is used in gunnery and targeting. Based upon an approximation of = 3.2, there are 6400 mils in a complete rotation. Other gunnery systems may use a different approximation to . Being based on the milliradian, it corresponds roughly to an error of 1 m at a range of 1000 m (at such small angles, the curvature is negligible). The divergence of laser beams is also usually measured in milliradians.
Smaller units like microradians (μrads) and nanoradians (nrads) are used in astronomy, and can also be used to measure the beam quality of lasers with ultra-low divergence. Similarly, the prefixes smaller than milli- are potentially useful in measuring extremely small angles.
Criticism
The widespread habit of expressing radians in terms of fractions of has been criticized because in this way one essentially use as a unit. An angle of radians represents half a circle, which appear to be a rather arbitrary choice of unit. Therefore various mathematicians and scientists have been critical of the custom of expressing radians as fractions of , and have proposed to use other constants instead. A. Eagle proposed to have a constant representing one quarter-turn. A constant representing 2 has been proposed because a circle is 2 radians around. Robert Palais proposed to use a "pi with three legs" () to denote 1 turn, while several people independently have proposed to use the Greek letter (tau) instead.
See also
References
External links
Category:Natural units Category:SI derived units Category:Trigonometry Category:Units of angle
af:Radiaal ar:راديان be-x-old:Радыян bo:གཞུ་ཚད། bs:Radijan bg:Радиан ca:Radian cs:Radián cy:Radian da:Radian de:Radiant (Einheit) et:Radiaan el:Ακτίνιο (μονάδα μέτρησης) es:Radián eo:Radiano eu:Radian fa:رادیان fr:Radian gl:Radián gan:弧度 ko:라디안 hr:Radijan id:Radian it:Radiante he:רדיאן ka:რადიანი kk:Радиан lv:Radiāns lt:Radianas mk:Радијан mr:त्रिज्यी ms:Radian nl:Radiaal (wiskunde) ja:ラジアン no:Radian nn:Radian pl:Radian pt:Radiano ro:Radian ru:Радиан si:රේඩියනය simple:Radian sk:Radián sl:Radian sr:Радијан sh:Radijan fi:Radiaani sv:Radian ta:ஆரையம் th:เรเดียน tg:Радиан uk:Радіан zh:弧度This text is licensed under the Creative Commons CC-BY-SA License. This text was originally published on Wikipedia and was developed by the Wikipedia community.
| Coordinates | 52°05′36″N5°7′10″N |
|---|---|
| name | Sean Price |
| background | solo_singer |
| alias | |
| birth date | March 17, 1972 |
| origin | Brownsville, Brooklyn, New York |
| genre | Hip Hop |
| years active | 1993-present |
| label | Duck Down |
| associated acts | Boot Camp Clik |
| website | }} |
Discography
Solo albums
| Title | Album details | Peak chart positions | ||||||||||||||
| ! scope="col" style="width:2.2em;font-size:90%;" | ! scope="col" style="width:2.2em;font-size:90%;" | ! scope="col" style="width:2.2em;font-size:90%;" | ||||||||||||||
| *Released: June 13, 2005 | *Label: Duck Down (#2011) | *Format: CD, digital download, LP | ||||||||||||||
| *Released: January 30, 2007 | *Label: Duck Down (#2045) | *Format: CD, digital download | ||||||||||||||
| *Released: TBA 2011 | *Label: Duck Down | |||||||||||||||
|
|
Singles |
|||||||||||||||
| + List of singles, with selected chart positions | Title | Year | Peak chart positions | Album |
| ! scope="col" style="width:3em;font-size:90%;" | ||||
Mixtapes
References
External links
Category:1972 births Category:Living people Category:African American rappers Category:Rappers from New York City Category:People from Brooklyn Category:Underground rappers Category:Boot Camp Clik members
es:Sean Price (rapero) fr:Sean Price it:Sean Price hu:Sean Price fi:Sean Price uk:Sean PriceThis text is licensed under the Creative Commons CC-BY-SA License. This text was originally published on Wikipedia and was developed by the Wikipedia community.



The World News (WN) Network, has created this privacy statement in order to demonstrate our firm commitment to user privacy. The following discloses our information gathering and dissemination practices for wn.com, as well as e-mail newsletters.
1. Personal Information Collection and Use
We do not collect personally identifiable information about you, except when you provide it to us. For example, if you submit an inquiry to us or sign up for our newsletter, you may be asked to provide certain information such as your contact details (name, e-mail address, mailing address, etc.).
When you submit your personally identifiable information through wn.com, you are giving your consent to the collection, use and disclosure of your personal information as set forth in this Privacy Policy. If you would prefer that we not collect any personally identifiable information from you, please do not provide us with any such information. We will not sell or rent your personally identifiable information to third parties without your consent, except as otherwise disclosed in this Privacy Policy.
Except as otherwise disclosed in this Privacy Policy, we will use the information you provide us only for the purpose of responding to your inquiry or in connection with the service for which you provided such information. We may forward your contact information and inquiry to our affiliates and other divisions of our company that we feel can best address your inquiry or provide you with the requested service. We may also use the information you provide in aggregate form for internal business purposes, such as generating statistics and developing marketing plans. We may share or transfer such non-personally identifiable information with or to our affiliates, licensees, agents and partners.
We may retain other companies and individuals to perform functions on our behalf. Such third parties may be provided with access to personally identifiable information needed to perform their functions, but may not use such information for any other purpose.
In addition, we may disclose any information, including personally identifiable information, we deem necessary, in our sole discretion, to comply with any applicable law, regulation, legal proceeding or governmental request.
2. E-mail addresses
We do not want you to receive unwanted e-mail from us. We try to make it easy to opt-out of any service you have asked to receive. If you sign-up to our e-mail newsletters we do not sell, exchange or give your e-mail address to a third party.
E-mail addresses are collected via the wn.com web site. Users have to physically opt-in to receive the wn.com newsletter and a verification e-mail is sent. wn.com is clearly and conspicuously named at the point of
collection.If you no longer wish to receive our newsletter and promotional communications, you may opt-out of receiving them by following the instructions included in each newsletter or communication or by e-mailing us at michaelw(at)wn.com
The security of your personal information is important to us. We follow generally accepted industry standards to protect the personal information submitted to us, both during registration and once we receive it. No method of transmission over the Internet, or method of electronic storage, is 100 percent secure, however. Therefore, though we strive to use commercially acceptable means to protect your personal information, we cannot guarantee its absolute security.
If we decide to change our e-mail practices, we will post those changes to this privacy statement, the homepage, and other places we think appropriate so that you are aware of what information we collect, how we use it, and under what circumstances, if any, we disclose it.
If we make material changes to our e-mail practices, we will notify you here, by e-mail, and by means of a notice on our home page.
3. Third Party Advertisers
The advertising banners and other forms of advertising appearing on this Web site are sometimes delivered to you, on our behalf, by a third party. In the course of serving advertisements to this site, the third party may place or recognize a unique cookie on your browser. For more information on cookies, you can visit www.cookiecentral.com.
4. Business Transfers
As we continue to develop our business, we might sell certain aspects of our entities or assets. In such transactions, user information, including personally identifiable information, generally is one of the transferred business assets, and by submitting your personal information on Wn.com you agree that your data may be transferred to such parties in these circumstances.



