In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees (marked with °). The equator has a latitude of 0°, the North pole has a latitude of 90° north (written 90° N or +90°), and the South pole has a latitude of 90° south (written 90° S or −90°). Together, latitude and longitude can be used as a geographic coordinate system to specify any location on the globe.

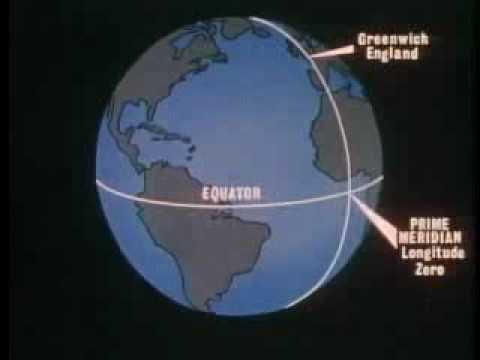
Curves of constant latitude on the Earth (running east-west) are referred to as lines of latitude. Each line of latitude is actually a circle on the Earth parallel to the equator, and for this reason lines of latitude are also known as ''circles of latitude'' or ''parallels''. In spherical geometry, lines of latitude are examples of circles of a sphere, with the equator being a great circle.

Latitude (usually denoted by the Greek letter phi (φ)) is often measured in degrees, with minutes and seconds for finer measurements. For example, the Eiffel Tower has a latitude of 48° 51′ 29″ N-- that is, 48 degrees plus 51 minutes plus 29 seconds. Alternatively, latitude may be measured entirely in degrees, e.g. 48.85806° N.

Examples

Named latitudes

Besides the equator, four other lines of latitude are commonly used to mark maps of the Earth. Each of these lines plays an important role in the geometrical relationship between the Earth and the Sun:

Arctic Circle: 66° 33′ 39″ N

Tropic of Cancer: 23° 26′ 21″ N

Equator: 0° Latitude

Tropic of Capricorn: 23° 26′ 21″ S

Antarctic Circle: 66° 33′ 39" S

Only at latitudes in the tropics is it possible for the sun to be directly overhead (at the zenith). Alternatively, only within the Arctic and Antarctic circles is it possible to have a polar night or midnight sun.

The latitudes of the two tropics are determined by the axial tilt of the Earth with respect to the sun, which is approximately 23° 26′ 21″. The latitudes of the Arctic and Antarctic circles are the complements to this angle.

Table of latitudes

The following table lists the regions of the Earth at various latitudes: :{| class="wikitable" |- ! Latitude ! Locations |- | 90° N | North pole |- | 75° N | Arctic ocean; northern Siberia, Russia; northern Canada; Greenland |- | 60° N | Oslo, Norway; St. Petersburg, Russia; Kenai, Alaska; Northwest territories in Canada |- | 45° N | France; Italy; Croatia; Serbia; Romania; the Black sea; Ukraine; the Caspian sea; Kazakhstan; northern China; Mongolia; northern Japan; Oregon, Maine in the United States; Ontario, Canada |- | 30° N | Morocco; Algeria; Libya; Egypt; Israel; Jordan; Saudi Arabia; Iraq; Kuwait; the Persian Gulf; Iran; Afghanistan; Pakistan; India; Nepal; southern China; southern Japan; northern Mexico; Texas, Florida, Louisiana in the United States |- | 15° N | Senegal; Mauritania; Mali; Burkina Faso; Niger; Chad; Sudan; Eritrea; the Red sea; Yemen; India; Myanmar (Burma); Thailand; Laos; Vietnam; Philippines; Northern Mariana Islands; southern Mexico; Guatemala; Honduras; Nicaragua; Cape Verde |- | 0° | São Tomé and Príncipe; Gabon; Republic of the Congo; Democratic Republic of the Congo; Uganda; Lake Victoria; Kenya; Somalia; Indonesia; Galápagos Islands and Quito, Ecuador; Colombia; Northern Brazil |- | 15° S | Angola; Zambia; Mozambique; Malawi; Madagascar; northern Australia; Vanatu; French Polynesia; Peru; Bolivia; Brazil |- | 30° S | South Africa; Lesotho; southern Australia; Chile; Argentina; Southern Brazil |- | 45° S | New Zealand; Chile; Argentina |- | 60° S | entirely ocean (slightly north of the South Orkney Islands); sometimes considered the northern boundary of the Southern ocean |- | 75° S | Dome C, Antarctica |- | 90° S | South pole |}

Subdivisions

A degree is divided into 60 minutes. One minute can be further divided into 60 seconds. An example of a latitude specified in this way is 13°19'43″ N (for greater precision, a decimal fraction can be added to the seconds). An alternative representation uses only degrees and minutes, where the seconds are expressed as a decimal fraction of minutes: the above example would be expressed as 13°19.717' N. Degrees can also be expressed singularly, with both the minutes and seconds incorporated as a decimal number and rounded as desired (decimal degree notation): 13.32861° N. Sometimes, the north/south suffix is replaced by a negative sign for south (−90° for the South Pole).

Effect of latitude

A region's latitude has a great effect on its climate and weather. Latitude more loosely determines prevailing winds, and other physical characteristics of geographic locations. Auroral activity is common at high geomagnetic latitudes.

Some observers have noted a correlation between the latitude of a country and its economic activity; see North-South divide.

Elliptic parameters

Because most planets (including Earth) are ''ellipsoids of revolution'', or spheroids, rather than spheres, both the radius and the length of arc varies with latitude. This variation requires the introduction of elliptic parameters based on an ellipse's angular eccentricity, $\backslash alpha\backslash ,\backslash !$ (which equals $\backslash arccos\backslash left(\backslash frac\{b\}\{a\}\backslash right)\backslash ,\backslash !$, where $a\backslash ;\backslash !$ and $b\backslash ;\backslash !$ are the equatorial radius (6,378,137.0 m for Earth) and the polar radius (6,356,752.3142 m for Earth), respectively; $\backslash sin^2(\backslash alpha)\backslash ,\backslash !$ is the first eccentricity squared, $\{e^2\}\backslash ,\backslash !$; and $2\backslash sin^2\backslash left(\backslash frac\{\backslash alpha\}\{2\}\backslash right)\backslash ;\backslash !$ or $1-\backslash cos(\backslash alpha)\backslash ,\backslash !$ is the flattening, $\{f\}\backslash ,\backslash !$. Utilized in creating the integrands for curvature is the inverse of the principal elliptic integrand, $E\text{'}\backslash ,\backslash !$:

::$n\text{'}(\backslash phi)=\backslash frac\{1\}\{E\text{'}(\backslash phi)\}\; =\backslash frac\{1\}\{\backslash sqrt\{1-(\backslash sin(\backslash phi)\backslash sin(\backslash alpha))^2\}\};\backslash ,\backslash !$ ::

Degree length

On Earth, the length of an arcdegree of north–south latitude difference, $\backslash scriptstyle\{\backslash Delta\backslash phi\}\backslash ,\backslash !$, is about 60 nautical miles, 111 kilometres or 69 statute miles at any latitude. The length of an arcdegree of east-west longitude difference, $\backslash scriptstyle\{\backslash cos(\backslash phi)\backslash Delta\backslash lambda\}\backslash ,\backslash !$, is about the same at the equator as the north-south, reducing to zero at the poles.

In the case of a spheroid, a meridian and its anti-meridian form an ellipse, from which an expression for the length of an arcdegree of latitude difference is: ::$\backslash frac\{\backslash pi\}\{180\}M(\backslash phi)\backslash ,\backslash !$ This radius of arc (or "arcradius") is in the plane of a meridian, and is known as the ''meridional radius of curvature'', $M\backslash ,\backslash !$.

Similarly, an expression for the length of an arcdegree of longitude difference is: ::$\backslash frac\{\backslash pi\}\{180\}\backslash cos(\backslash phi)N(\backslash phi)\backslash ,\backslash !$ The arcradius contained here is in the plane of the prime vertical, the east-west plane perpendicular (or "normal") to both the plane of the meridian and the plane tangent to the surface of the ellipsoid, and is known as the ''normal radius of curvature'', $N\backslash ,\backslash !$.

Along the equator (east-west), $N\backslash ;\backslash !$ equals the equatorial radius. The radius of curvature at a right angle to the equator (north-south), $M\backslash ;\backslash !$, is 43 km shorter, hence the length of an arcdegree of latitude difference at the equator is about 1 km less than the length of an arcdegree of longitude difference at the equator. The radii of curvature are equal at the poles where they are about 64 km greater than the north-south equatorial radius of curvature ''because'' the polar "radius" is 21 km less than the equatorial radius. The shorter polar radii indicate that the northern and southern hemispheres are flatter, making their radii of curvature longer. This flattening also 'pinches' the north-south equatorial radius of curvature, making it 43 km less than the equatorial radius. Both radii of curvature are perpendicular to the plane tangent to the surface of the ellipsoid at all latitudes, directed toward a point on the polar axis in the opposite hemisphere (except at the equator where both point toward Earth's center). The east-west radius of curvature reaches the axis, whereas the north-south radius of curvature is shorter at all latitudes except the poles.

The WGS84 ellipsoid, used by all GPS devices, uses an equatorial radius of and an inverse flattening, (1/f), of , hence its polar semi-axis is and its first eccentricity squared is . The more recent but little used IERS 2003 ellipsoid provides equatorial and polar semi-axes of and , respectively, and an inverse flattening of . Lengths of degrees on the WGS84 and IERS 2003 ellipsoids are the same when rounded to six significant digits. An appropriate calculator for any latitude is provided by the U.S. government's National Geospatial-Intelligence Agency (NGA).

On the WGS84 spheroid, the length in meters of a degree of latitude at latitude φ (that is, the distance along a north-south line from latitude (φ - 0.5) degrees to (φ + 0.5) degrees) is about

111132.954 - 559.822(cos 2φ) + 1.175(cos 4φ)

(Those coefficients can be improved, but as they stand the distance they give is correct within a centimeter.)

!Latitude 6335.44 km 6339.70 km 6351.38 km 6367.38 km 6383.45 km 6395.26 km 6399.59 km

|	N-S radiusof curvature $M\backslash ;\backslash !$	Surface distance per 1° change in latitude		E-W radius of curvature$N\backslash ;\backslash !$	Surface distance per 1° change in longitude
0°	|	110.574 km		6378.14 km	111.320 km
15°	|	110.649 km		6379.57 km	107.551 km
30°	|	110.852 km		6383.48 km	96.486 km
45°	|	111.132 km		6388.84 km	78.847 km
60°	|	111.412 km		6394.21 km	55.800 km
75°	|	111.618 km		6398.15 km	28.902 km
90°	|	111.694 km		6399.59 km	0.000 km

Auxiliary latitudes

There are six auxiliary latitudes that have applications to special problems in geodesy, geophysics and the theory of map projections: :* geocentric latitude, :* reduced (or parametric) latitude, :* authalic latitude, :* rectifying latitude, :* conformal latitude, :* isometric latitude. When the word 'latitude' is used without qualification it is to be taken as the geodetic latitude, sometimes called the geographic latitude.

All the auxiliary latitudes, except the isometric latitude, are numerically close to the geodetic latitude, the difference being zero at the poles and on the equator and attaining a maximum, between 5 and 10 minutes of arc, at a geodetic latitude a few arc minutes from 45 degrees. The geodetic latitude is greater than (or equal to) all auxiliary latitudes.

In the theory of map projections the auxiliary latitudes are typically employed as intermediate constructs in a transformation from geodetic coordinates to Eastings and Northings in the projection plane. The end user has no need of a numerical value such as the authalic latitude of the Eiffel tower.

The auxiliary latitudes defined below have been expressed in terms of the semi-major axis, ''a'', and the eccentricity, ''e'', in forms which agree, apart from notational variants, with those given in the standard reference for map projections, namely ''Map projections — a working manual'' by Snyder. Derivations which assume some knowledge of the geometrical properties of the ellipsoid may be found in Adams. Pedagogical discussions of the geometry of the ellipsoid may be found in Rapp (Chapter 3) and Osborne (Chapters 5,6)

Geocentric latitude

The geocentric latitude, denoted here by ψ, is the angle between the equatorial plane and the radius from the centre to a point on the surface. The relation between the geodetic latitude ($\backslash phi$) and the geocentric latitude ($\backslash psi$) is ::$\backslash psi(\backslash phi)=\backslash arctan\backslash left[(1-e^2)\backslash tan\backslash phi\backslash right]\backslash ;\backslash !.$ The geodetic and geocentric latitudes are equal at the equator and poles. The value of the squared eccentricity is approximately 0.007 (depending on the choice of ellipsoid) and the maximum difference of $(\backslash phi-\backslash psi)$ is approximately 11.5 minutes of arc at a geodetic latitude of 45°6′.

Reduced (or parametric) latitude

The reduced or parametric latitude, β, is defined by the radius drawn from the centre of the ellipsoid to that point on the surrounding sphere (of radius ''a'') which is the vertical projection (parallel to Earth's axis of rotation) of a point on the ellipsoid at latitude $\backslash scriptstyle\backslash phi$. It was so-called by Bessel who solved problems for geodesics on the ellipsoid by reducing them to the equivalent problem on the sphere. It is widely used in the theory of projections. In terms of the geodetic latitude ::$\backslash beta(\backslash phi)=\backslash arctan\backslash left[\backslash sqrt\{1-e^2\}\backslash tan\backslash phi\backslash right]\backslash ,\backslash !$ The alternative name arises from the parameterization of the equation of the ellipse describing a meridian section. In terms of Cartesian coordinates ''p'', the distance from the axis, and ''z'', the distance above the equatorial plane, the equation of the ellipse is ::$\backslash frac\{p^2\}\{a^2\}\; +\; \backslash frac\{z^2\}\{b^2\}\; =1\; .$ The Cartesian coordinates of the point are parameterized by ::$p=a\backslash cos\backslash beta,\; \backslash qquad\; z=b\backslash sin\backslash beta.$

Authalic latitude

The authalic latitude, ξ, gives an area-preserving transformation to a sphere. ::$\backslash xi(\backslash phi)=\backslash arcsin\backslash left(\backslash frac\{q(\backslash phi)\}\{q\_p\}\backslash right)\backslash ,\backslash !$ where ::$q(\backslash phi)=\; \backslash frac\{(1\; -\; e^2)\backslash sin\backslash phi\}\{1\; -\; e^2\; \backslash sin^2\; \backslash phi\}\; -\backslash frac\{1-e^2\}\{2e\}\backslash ln\; \backslash left(\backslash frac\{1-e\backslash sin\backslash phi\}\{1+e\backslash sin\backslash phi\}\backslash right),$ and ::$q\_p\; =\; q(\backslash pi/2)\; =1-\backslash frac\{1-e^2\}\{2e\}\backslash ln\; \backslash left(\backslash frac\{1-e\}\{1+e\}\backslash right),\backslash ,$ and the radius of the sphere is taken as ::$R\_q=a\backslash sqrt\{q\_p/2\}.\backslash ,$ Using the authalic latitude as a latitude on a sphere of the above radius defines an equal area mapping from the ellipsoid to the sphere. If the sphere is then projected to the plane with an area projection the result is an area-preserving double projection from the ellipsoid to the plane.

Rectifying latitude

The rectifying latitude, μ, is the meridian distance scaled so that its value at the poles μ is equal 90 degrees or π/2 radians: :: $\backslash mu(\backslash phi)=\backslash frac\{\backslash pi\}\{2\}\backslash frac\{m(\backslash phi)\}\{m\_p\}\backslash ,\backslash !$ where the meridian distance from the equator to a latitude φ is (see Meridian arc) ::$m(\backslash phi)=\; a(1\; -\; e^2)\backslash int\_0^\backslash phi\; \backslash left\; (1\; -\; e^2\; \backslash sin^2\; \backslash phi\; \backslash right\; )^\{-3/2\}\; d\backslash phi,$ and the length of the meridian quadrant to the pole is ::$m\_p\; =\; m(\backslash pi/2).\backslash ,$ Using the rectifying latitude to define a latitude on a sphere of radius ::$R=\backslash frac\{2m\_p\}\{\backslash pi\}$ defines a projection from the ellipsoid to the sphere such that all meridians have true length and uniform scale. The sphere may then be projected to the plane with an equirectangular projection to give a double projection from the ellipsoid to the plane such that all meridians have true length and uniform meridian scale.

Conformal latitude

The conformal latitude, χ, gives an angle-preserving (conformal) transformation to the sphere. ::$\backslash chi(\backslash phi)=2\backslash arctan\backslash left[\; \backslash left(\backslash frac\{1+\backslash sin\backslash phi\}\{1-\backslash sin\backslash phi\}\backslash right)\; \backslash left(\backslash frac\{1-e\backslash sin\backslash phi\}\{1+e\backslash sin\backslash phi\}\backslash right)^\{\backslash !\backslash textit\{e\}\}\; \backslash ;\backslash right]^\{1/2\}\; -\backslash frac\{\backslash pi\}\{2\}\; \backslash ;\backslash !$. This expression is sometimes given in the form ::$\backslash chi(\backslash phi)=2\backslash arctan\backslash left[\; \backslash tan\backslash left(\backslash frac\{\backslash phi\}\{2\}+\backslash frac\{\backslash pi\}\{4\}\backslash right)\; \backslash left(\backslash frac\{1-e\backslash sin\backslash phi\}\{1+e\backslash sin\backslash phi\}\backslash right)^\{\backslash !\backslash textit\{e\}/2\}\; \backslash ;\backslash right]\; -\backslash frac\{\backslash pi\}\{2\}\; \backslash ;\backslash !$. This kind of latitude defines a transformation from the ellipsoid to a sphere of ''arbitrary'' radius such that the angle of intersection between any two lines on the ellipsoid is the same as the corresponding angle on the sphere (so that the shape of ''small'' elements is well preserved). A further conformal transformation from the sphere to the plane gives a conformal double projection from the ellipsoid to the plane. This is not the only way of generating such a conformal projection. For example, the 'exact' version of the Transverse Mercator projection on the ellipsoid is not a double projection. (It does, however, involve a generalisation of the conformal latitude to the complex plane).

Isometric latitude

The isometric latitude, ψ (not to be confused with the geocentric latitude notation), is very important in the development of the ellipsoidal versions of the normal Mercator projection and the Transverse Mercator projection. The name "isometric" arises from the fact that at any point on the ellipsoid equal increments of ψ and longitude λ give rise to equal distance displacements along the meridians and parallels respectively. The graticule defined by the lines of constant ψ and constant λ, divides the surface of the ellipsoid into a mesh of squares (of varying size). The isometric latitude is zero at the equator but rapidly diverges from the geodetic latitude, tending to infinity at the poles. The conventional notation is given in Snyder: ::$\backslash psi(\backslash phi)\; =\backslash ln\backslash left[\backslash tan\backslash left(\; \backslash frac\{\backslash pi\}\{4\}+\backslash frac\{\backslash phi\}\{2\}\backslash right)\; \backslash right]\; +\; \backslash frac\{e\}\{2\}\backslash ln\backslash left[\; \backslash frac\{1-e\backslash sin\backslash phi\}\{1+e\backslash sin\backslash phi\}\; \backslash right]$ For the ''normal'' Mercator projection (on the ellipsoid) this function defines the spacing of the parallels: if the length of the equator on the projection is E (units of length or pixels) then the distance, ''y'', of a parallel of latitude φ from the equator is ::$y(\backslash phi)=\backslash frac\{E\}\{2\backslash pi\}\backslash psi(\backslash phi).$

Comparison of selected types

The following plot shows the differences between the types of latitude. The data used are found in the table following the plot. Please note that the values in the table are in minutes, not degrees, and the plot reflects this as well. Also observe that the conformal symbols are hidden behind the geocentric due to being very close in value. Finally it is important to mention also that these differences don't mean that the use of one specific latitude will necessarily cause more distortions than the other (the real fact is that each latitude type is optimized for achieving a different goal).

:{| class="wikitable" !colspan="6"|Approximate difference from geographic latitude ("Lat") |- !Lat$\backslash phi\backslash ,\backslash !$ !Reduced$\backslash phi-\backslash beta\backslash ,\backslash !$ !Authalic$\backslash phi-\backslash xi\backslash ,\backslash !$ !Rectifying$\backslash phi-\backslash mu\backslash ,\backslash !$ !Conformal$\backslash phi-\backslash chi\backslash ,\backslash !$ !Geocentric$\backslash phi-\backslash psi\backslash ,\backslash !$ |- |0° || 0.00′|| 0.00′|| 0.00′|| 0.00′|| 0.00′ |- |5° || 1.01′|| 1.35′|| 1.52′|| 2.02′|| 2.02′ |- |10°|| 1.99′|| 2.66′|| 2.99′|| 3.98′|| 3.98′ |- |15°|| 2.91′|| 3.89′|| 4.37′|| 5.82′|| 5.82′ |- |20°|| 3.75′|| 5.00′|| 5.62′|| 7.48′|| 7.48′ |- |25°|| 4.47′|| 5.96′|| 6.70′|| 8.92′|| 8.92′ |- |30°|| 5.05′|| 6.73′|| 7.57′||10.09′||10.09′ |- |35°|| 5.48′|| 7.31′|| 8.22′||10.95′||10.96′ |- |40°|| 5.75′|| 7.66′|| 8.62′||11.48′||11.49′ |- |45°|| 5.84′|| 7.78′|| 8.76′||11.67′||11.67′ |- |50°|| 5.75′|| 7.67′|| 8.63′||11.50′||11.50′ |- |55°|| 5.49′|| 7.32′|| 8.23′||10.97′||10.98′ |- |60°|| 5.06′|| 6.75′|| 7.59′||10.12′||10.13′ |- |65°|| 4.48′|| 5.97′|| 6.72′|| 8.95′|| 8.96′ |- |70°|| 3.76′|| 5.01′|| 5.64′|| 7.52′|| 7.52′ |- |75°|| 2.92′|| 3.90′|| 4.39′|| 5.85′|| 5.85′ |- |80°|| 2.00′|| 2.67′|| 3.00′|| 4.00′|| 4.01′ |- |85°|| 1.02′|| 1.35′|| 1.52′|| 2.03′|| 2.03′ |- |90°|| 0.00′|| 0.00′|| 0.00′|| 0.00′|| 0.00′ |}

Corrections for altitude

When converting from geodetic ("common") latitude to other types of latitude, corrections must be made for altitude for systems which do not measure the angle from the normal of the spheroid. For example, in the figure at right, point ''H'' (located on the surface of the spheroid) and point ''H''' (located at some greater elevation) have different ''geocentric'' latitudes (angles ''β'' and ''γ'' respectively), even though they share the same ''geodetic'' latitude (angle ''α''). Note that the flatness of the spheroid and elevation of point ''H''' in the image is significantly greater than what is found on the Earth, exaggerating the errors inherent in such calculations if left uncorrected. Note also that the reference ellipsoid used in the geodetic system is itself just an approximation of the true geoid, and therefore introduces its own errors, though the differences are less severe. (See Astronomical latitude, below.)

Astronomical latitude

A fundamentally different measure of latitude is the astronomical latitude, which is the angle between the equatorial plane and the normal to the geoid (i.e. a plumb line). This is the only "latitude" that is not based on the spheroid being used to approximate the Earth's surface. It differs from the geodetic latitude only slightly (usually not more than a few thousandths of a degree) due to the slight deviations of the geoid from the reference ellipsoid.

Astronomical latitude is not to be confused with declination, the coordinate astronomers use to describe the locations of stars north/south of the celestial equator (see equatorial coordinates), nor with ecliptic latitude, the coordinate that astronomers use to describe the locations of stars and solar system bodies north/south of the ecliptic (see ecliptic coordinates).

Paleolatitude

Continents move over time, due to continental drift, taking whatever fossils and other features of interest they may have with them. Particularly when discussing fossils, it is often more useful to know where the fossil was when it was laid down, than where it is when it was dug up: this is called the ''paleolatitude'' of the fossil. The paleolatitude can be constrained by paleomagnetic data. If tiny magnetisable grains are present when the rock is being formed, these will align themselves with Earth's magnetic field like compass needles. A magnetometer can deduce the orientation of these grains by subjecting a sample to a magnetic field, and the magnetic declination of the grains can be used to infer the latitude of deposition.

See also

Footnotes

External links

GEONets Names Server, access to the National Geospatial-Intelligence Agency's (NGA) database of foreign geographic feature names.

Look-up Latitude and Longitude

Resources for determining your latitude and longitude

Convert decimal degrees into degrees, minutes, seconds - Info about decimal to sexagesimal conversion

Convert decimal degrees into degrees, minutes, seconds

Latitude and longitude converter – Convert latitude and longitude from degree, decimal form to degree, minutes, seconds form and vice versa. Also included a farthest point and a distance calculator.

Distance calculation based on latitude and longitude - JavaScript version

Determination of Latitude by Francis Drake on the Coast of California in 1579

Lines of latitude Category:Geodesy Category:Navigation

af:Breedtegraad als:Geografische Breite ar:دائرة عرض ast:Llatitú bn:অক্ষাংশ zh-min-nan:Hūi-tō͘ be-x-old:Шырата bs:Geografska širina br:Led bg:Географска ширина ca:Latitud ceb:Latitud cs:Zeměpisná šířka cy:Lledred de:Geographische Breite et:Laiuskraad el:Γεωγραφικό πλάτος es:Latitud eo:Latitudo eu:Latitude fa:عرض جغرافیایی fr:Latitude fy:Breedtegraad gl:Latitude ko:위도 hi:अक्षांश रेखाएं hr:Zemljopisna širina io:Latitudo ig:Latitude id:Garis lintang os:Уæрхад is:Breiddargráða it:Latitudine he:קו רוחב kn:ಅಕ್ಷಾಂಶ kk:Ендік sw:Latitudo ht:Latitid ku:Hêlîpan lo:ເສັ້ນຂະໜານ la:Latitudo geographica lv:Ģeogrāfiskais platums lb:Breedegrad lt:Platuma ln:Monkɔlɔ́tɔ mwâ libale mk:Латитуда ml:അക്ഷാംശം mr:अक्षांश ms:Latitud nl:Breedtegraad nds-nl:Breedtegraod ne:अक्षांश ja:緯度 no:Breddegrad nn:Breiddegrad mhr:Лоптык pl:Szerokość geograficzna pt:Latitude ro:Latitudine ru:Широта sah:Кэтирээһин sq:Gjerësia gjeografike scn:Latitùdini simple:Latitude sk:Zemepisná šírka sl:Zemljepisna širina sr:Географска ширина su:Garis Datar fi:Leveyspiiri sv:Latitud tl:Latitud ta:நிலநேர்க்கோடு te:రేఖాంశం th:ละติจูด tr:Enlem uk:Широта ur:عرض البلد vec:Latitudine vi:Vĩ độ vls:Brêedtegroad wo:Tus-wu-gaar yi:גארטל ליניע (געאגראפיע) zh:纬度