Image Source.
Everything that we know about planet formation indicates that both Alpha Centauri A and Alpha Centauri B should be accompanied by terrestrial planet systems. Long-term integrations show that the dynamical environment is stable. Simulations using the Wetherill-Chambers method show that the accretion of terrestrial-sized bodies should proceed with an equal or greater ease than was the case in our own solar system. The metallicity of Alpha Centauri is significantly supersolar, which points toward the availability of plenty of raw material for forming terrestrial planets.
The terrestrial planets orbiting Alpha Centauri A and B were likely assembled from dried-out planetesimals. Pertubations from Proxima, however, would have stirred up Alpha Centauri’s circumbinary analog of the Kuiper belt, providing a mechanism for the delivery of volatiles to terrestrial bodies orbiting A and B.
In a string of posts last month [most recent here], we laid out the case for the existence of terrestrial planets in the Alpha Centauri system. We argued that if one of these planets has an Earth-mass and a habitable orbit, then it is detectable with a flat-out effort by the HARPS spectrograph. We based our argument on the fact that HARPS was recently used to produce an amazing detection of three Neptune-mass worlds orbiting HD 69830 — an old, chromospherically quiet K0V star that is a near-exact twin of Alpha Centauri B.
This presents quite an interesting situation. HARPS, at La Silla, and the AAT in Australia are the only instruments in the world that currently could conceivably be used to make the detection. The APF telescope can’t see the Southern Sky, and the wider astronomical community would never allow one of the VLTs to be commandered for an all-out effort on one charismatic system. Furthermore, both HARPS and AAT are currently hard at work on large-scale radial velocity surveys. This means that [1] we’re unlikely to get scooped, and [2] we’ll have to build a special-purpose telescope if we want to explore the Alpha Centauri planetary system.
Eugenio and Aaron and I have begun a detailed feasibility study of a dedicated, state-of-the-art radial velocity campaign on Alpha Centauri B. So far, the results have been encouraging — nothing resembling a showstopper has turned up yet. The purpose of the next few posts is to report what we’ve learned so far. We’ll be posting data files so that interested readers can replicate (and if they want to, extend) our work using either their own routines or the downloadable systemic console.
We’re extremely lucky to have a metal-rich KOV dwarf star lying just 1.3 parsecs away. Alpha Centauri B is roughly 100 times brighter than any other equally desirable radial velocity candidate star. The presence of Alpha Centauri A on its 80 year orbit, however, poses a complication for the fitting procedure of radial velocities from B. This problem seems readily solvable, however, and we’ll examine it in much more depth in one of the upcoming posts. Here, we’ll assume that the long-term large-amplitude radial velocity signal arising from A has been correctly filtered out of the data.
Our first step, then, was to invent some terrestrial planetary systems. Our systems have been produced with a Wetherill-Chambers method accretion code, and are both dynamically stable, and organically farmed in the Alpha Centauri AB environment.
Once a terrestrial planetary system has been created, it is observed with Eugenio’s TAC code. The TAC code is provided with a location on Earth (we’re producing synthetic data from telescopes located at La Silla and at the South Pole), and the position of the target star on the sky. Based on the readout time for the HARPS spectrograph, we assume an observing cadence of 200 seconds. Radial velocities are obtained whenever (1) the simulated weather is clear, (2) the Sun is more than 102 degrees from the zenith, and (3) Alpha Centauri is at less than 2.5 air masses. With its declination of -60 degrees, Alpha Centauri is circumpolar at La Silla, which significantly improves its overall observability. Observational errors are drawn from a normal distribution implied by the RMS residuals to the HD 69830 fit. We’re proactively aware that this is only a first approximation. (Over at my other job, we’ve been spending a fair amount of time thinking about autoregressive conditional heteroskedasticity.)
After running the TAC code, we find that 96,464 radial velocities are obtained in a trial five-year observing session. That’s one helluva RV data set. The complete time series has been added to the datafiles directory of the downloadable systemic console. You can access it by selecting “other” from the bottom of the system menu and opening the file AlphaCenB_Y5.sys. Note that because of the large size of this data set, the console function will be very slow. Patience is required. If you want to use your own software, the time series is AlphaCenB_Y5.vels.
When 96,076 velocities are all displayed in the data window, the resulting plot shows the yearly modulation of observability:

If you zoom to the highest time resolution, you can see the blocks of radial velocities obtained on successive nights:

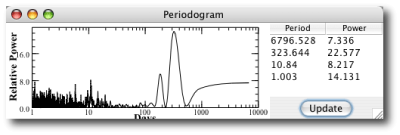
The periodogram says it all:

The peak at 351 days corresponds to a half Earth-mass planet. The three neighboring peaks correspond to smaller planets having masses on the order of Mars.
Aaron tweaked the code for the folding window so that large datasets can be usefully manipulated. When the data is folded at 351 days, the periodicity is ever so faintly visible. Thanks to Joseph Fourier, however, the planets are clearly, unmistakeably detectable in the periodogram.
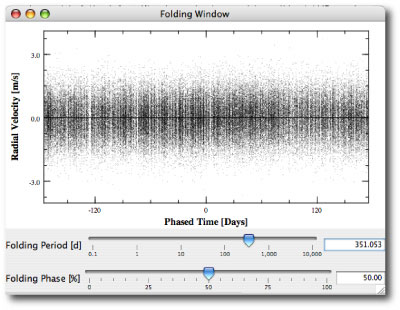
In the upcoming posts, we’ll talk in detail about the results of fitting to this data, and how the fit compares to the actual planetary system under observation. We’ll also look at modeling systematic error, non-gaussian noise, uncertainty, biases and so forth. These complications will inevitably erode the size of the peak in the above periodogram. Then we’ll implement a double-blind experiment on a set of 10 individual time series. Then we’ll talk about the confounding factors introduced by the binary companion. Then we’ll talk strategy.















 .
.