systemic

That Sunday Afternoon Feeling7
greg posted in worlds on November 30th, 2008

Academics across the United States know the feeling at the end of the long Thanksgiving weekend. Four days were to be given over (at least partially) to catching up with a long list of slipped deadlines and overdue tasks. Like the last line of a haiku, Sunday afternoon arrives.

The red dwarf stars, on the other hand, have mastered the art of having enough time. A trillion years from now, the science of extragalactic astronomy will have long since ended, but Proxima Centauri, our nearest stellar neighbor, will be shining more or less unaltered from its current recessionista persona.

Proxima will never turn into a red giant. Like the other low-mass red dwarfs, it will grow steadily brighter and bluer as it ages, eventually turning itself into a helium white dwarf that gradually cools and fades to black.

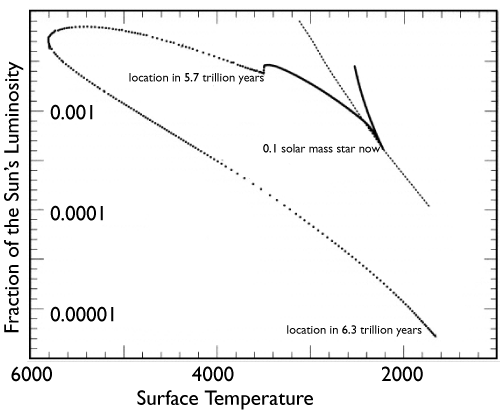
The galaxy is filled with red dwarfs, and so as a result, the total luminosity of the Milky Way will stay surprisingly constant for a long time to come. A few years ago, Fred Adams, Genevieve Graves and I wrote a conference proceedings that looks in detail at the future luminosity evolution of the galaxy.

As the Milky Way’s stellar population ages, the more massive stars (The Sun, Sirius, Alpha Cen A & B, Tau Ceti et al.) die off. For hundreds of billions of years, their flagging contributions to the galactic luminosity are very nearly compensated by the increase in luminosity of smaller stars. This state of affairs will persist until about 800 billion years from now, at which time the remaining main sequence stars will all have less than ~30% of the solar mass. These stars never experience the large luminosity increase associated with the red giant phase, and the galactic light curve declines gently for about 7 trillion years as the lowest mass stars slowly die. During this long autumn, the galaxy as a whole should look quite blue, because the light is dominated by stars that have aborted their journey up the red giant branch and grown bluer. Eventually, after about 8 trillion years, even the smallest stars have run out of hydrogen and the night sky finally goes black for the duration.

Just trying to put the arrival of Monday morning in perspective.

Sirius3
greg posted in worlds on November 25th, 2008

When I got home last Saturday, Sirius had just risen above the neighbors’ roof. The air was dramatically clear. In spite of the Santa Cruz city lights, I could make out stars down to fourth magnitude. The seeing, however, must have been incredibly bad, with a large amount of turbulence at high altitude. Sirius was twittering stochastically from white and blue to brief moments of intense, unmistakable fire-engine orange. Scintillation has got to be at the root of the red Sirius anomaly.

The back of every introductory astronomy textbook contains separate one-page lists of the nearest stars to the Sun and the brightest stars in the sky. I’ve never paid much attention to the lists of brightest stars. Rigel, Deneb, and Hadar are hundreds of parsecs away, hot-tempered, short-lived and ultimately rather tiresome. It’s more interesting to pore over the lists of nearest stars. Alpha Centauri, Eta Cassiopeiae, Tau Ceti, 61 Cygni, Barnard’s star…

It’s always seemed odd to me that Sirius and Alpha Cen are at or near the top of both lists. Sirius, the brightest star in the sky, is in the fifth-nearest system, and Alpha Cen A, the fourth-brightest star is in the nearest system. It’s as if Henry Winkler lived three houses down your street in one direction and Barry Manilow lived five houses up the street in the other direction.

Over a lifetime, the constellations seem fixed, but on geologic timescales, the Sun rapidly drifts through completely new lists of nearest stellar neighbors. A kilometer per second is a parsec in a million years, and stars in the solar neighborhood have a velocity dispersion of ~30 km/sec. This means that the list of nearest 100 stellar systems undergoes a complete turnover roughly every 300,000 years, and over Earth’s 4.5 billion year lifetime, the tables in the back of the Astronomy 101 textbooks have gone through thousands of completely different editions.

The Hipparcos catalog multi-parameter search tool lists 1549 stars with distances less than 25 parsecs. For stars like Alpha Cen B and Sirius, this list is complete. That is, if we go out to 25 parsecs, we know about all the K0V stars, whereas the census of the lowest-mass (and hence extremely dim) red dwarfs is significantly incomplete beyond five parsecs or so. The 1549 nearest stars in the Hipparcos catalog all have their apparent V magnitudes listed and these are easily converted to absolute magnitudes since the distances are known to high accuracy. With the absolute magnitudes in hand, I wrote a short program that repeatedly draws new random 3D distributions of the 1549 stars within our 25-parsec sphere. By doing this, it’s possible to get a sense of how unusual it is to have stars like Sirius and Alpha Cen B essentially right next door. Given that this is just a blog post, I ignored any modifying effects arising from individual stars adhering into binary and multiple systems.

First, Sirius. I ran 1,000 trials, and filtered for instances in which a star that is instrinsically as bright or brighter than Sirius lies as close or closer than Sirius’ current 2.64-parsec distance. This condition was satisfied in 31 of the trials, and in one trial, two stars fit the bill. In a rough sense, then, the presence of Sirius is “unusual” at the 3% level.

As Oklo readers are no doubt aware, I’m rooting for a high-cadence Doppler velocity campaign on Alpha Cen B. The relevant question in this case is: What are the odds that we have a stellar neighbor that is as visibly bright or brighter than Alpha Cen B (V<1.34) with an absolute magnitude equal to or fainter than B (Mv>5.71)? We want a bright star so that a smaller telescope can be used, and so that a maximum number of observations can be made. We want an intrinsically dimmer cooler star because the radial velocity method works at the peak of its ability with K-type dwarfs, and because the radial velocity half-amplitude at given mass is larger and because the habitable zone is closer to the star.

Interestingly, adopting this criterion, Alpha Cen B is also unusual at the 3% level. In 1000 trials, a star that’s intrinsically dimmer than Alpha Cen B that (as a result of proximity) is visibly brighter on the sky occurred 28 times, and in one instance, two such stars made the grade.

Alpha Cen B is special for a number of other reasons: (1) metallicity, (2) binary plane orientation, (3) presence of Alpha Cen A as a control star, (4) sky position, (5) age. It’s sort of like having it turn out that Bono lives right next door.

Chance favors the prepared mind.0
greg posted in worlds on November 21st, 2008

I was reading a newspaper article last weekend, and ran across one of the more satisfying aphorisms. Chance favors the prepared mind. I just like the ring of that.

Along roughly similar lines, it’s curiously inspiring when someone gets a great, lucky opportunity, and then really steps up to the plate and knocks the ball out of the park. I’ve been trying to identify the best examples of this phenomenon. Consider, for example, when Brian Johnson was offered the lead vocal for AC DC. It’s hard to argue with worldwide sales of 42 million for Back in Black.

What about instances drawn from Astronomy? Johannes Kepler jumps to mind, but everyone already knows the the raft of Copernicus-Brahe-Galileo-Kepler anecdotes. I like the story of Joseph Fraunhofer (lifted from Wikipedia):

Fraunhofer was born in Straubing, Bavaria. He became an orphan at the age of 11, and he started working as an apprentice to a harsh glassmaker named Philipp Anton Weichelsberger. In 1801 the workshop in which he was working collapsed and he was buried in the rubble. The rescue operation was led by Maximilian IV Joseph, Prince Elector of Bavaria (the future Maximilian I Joseph). The prince entered Fraunhofer’s life, providing him with books and forcing his employer to allow the young Joseph Fraunhofer time to study.

After eight months of study, Fraunhofer went to work at the Optical Institute at Benediktbeuern, a secularised Benedictine monastery devoted to glass making. There he discovered how to make the world’s finest optical glass and invented incredibly precise methods for measuring dispersion. In 1818 he became the director of the Optical Institute. Due to the fine optical instruments he had developed, Bavaria overtook England as the centre of the optics industry. Even the likes of Michael Faraday were unable to produce glass that could rival Fraunhofer’s.

The quality of Fraunhofer’s optics played a large role in providing Bessel with the precision that he needed to measure the parallax of 61 Cygni. In explicitly demonstrating the staggering distances to the stars, Bessel was able to bring to a 200+ year scientific quest to a dramatic finish. Hard to argue with that.

Alpha Cen Bb…10
greg posted in worlds on November 18th, 2008

Anybody who knows anything about candy knows that “fun size” isn’t any fun at all. The same is true for terrestrial planets. Fun size objects like Mercury, the Moon, Ceres, Vesta and Pallas are airless cratered and dead.

For the past several years, I’ve been agitating for a dedicated radial velocity search for potentially habitable King-size terrestrial planets in the Alpha Centauri system. A number of factors (brightness, age, spectral type, metallicity, orientation, and sky position) make Alpha Cen B overwhelmingly best star in the sky for detecting habitable planets from the ground and on the cheap.

Planets are dynamically stable in the habitable zone of Alpha Cen B. It’s also true that if one starts with hundreds of lunar-sized embryos in the Alpha Cen system, then the formation of King-size terrestrial planets is effectively a given.

But there’s a snag. Those embryos may never have formed. Recent work by Philippe Thebault and his collaborators makes a case that the Alpha Centauri system provided an unfavorable environment for the accretion of planetary embryos, and as a result, the prospects for finding a habitable planet right next door may be depressingly slim. Thebault et al’s first paper (here) clears out the planets around A, and their second paper, which came out at the beginning of this month (here), deals effectively with B.

The basic idea works like this. During the epoch when kilometer-sized bodies are trying to accrete and grow, the presence of a binary stellar perturber forces planetesimal orbits in the circumprimary disks to be eccentric. This eccentricity forcing occurs in the presence of gas drag on the planetesimals. For a population of equal-mass bodies, gas drag and gravitational forcing cause the periastra of the planetesimal orbits to line up. When such phasing occurs, neighboring particles have small relative velocities, collisions are gentle, and the planetesimals are able to grow via collisional agglomeration.

Unfortunately, both the forced eccentricity and the phase angle relative to the binary periastron depend on planetesimal mass. If the disk contains bodies of different sizes, then one gets crossing orbits and larger collision velocities. Planetesimals don’t stick together when they’re bashed together.

Thebault and his collaborators sum up their bottom line results in the following table (which I’ve clipped directly out of their Alpha Cen B paper):

The column on the left lists the initial conditions. The column on the right gives the radius beyond which construction of embryos is thwarted. Conditions that are consistent with the disk that gave rise to our Solar System are encapsulated in the “minimum-mass solar nebula” (MMSN) nominal case. When the MMSN is used as an initial condition for Alpha Cen B, the region exterior to 0.5 AU is unfriendly to accretion. In order for embryos to form in the habitable zone, one’s best bet is to crank up the disk gas density by a factor of at least several. (The table indicates that a 10xMMSN initial conditions allows embryos to form all the way out to 0.8 AU).

Even when confronted with these results, I’m still cautiously long Alpha Cen Bb. It’s not that I think the simulations are wrong or that there is any problem with the outcomes that they produce. Rather, I don’t think a high gas density in the inner AU of the Alpha Cen B disk is cause for alarm. In a nutshell, I don’t see evidence that the MMSN is of any particular utility for explaining the extrasolar planetary systems that we’ve found so far, and hence I’m not depressed that high gas densities were required for Alpha Cen B to have fostered an accretion-friendly environment. Reconstitute, for example, the HD 69830 protoplanetary disk or the 55 Cnc protoplanetary disk. I’m plain skeptical of the validity of a fiducial MMSN scaling for the disks that orbited the Alpha Cen stars. The Alpha Cen binary has twice the total mass of the Solar System, and more than two thousand times the total angular momentum.

We need to do the experiment and find out what’s really there.

6D plotting1
greg posted in worlds on November 16th, 2008

As more and more extrasolar planets are characterized, the correlation diagrams steadily increase in their intrinsic appeal. Each planet is attached to a number of interesting quantities (planetary Msin(i), period, and eccentricity, and parent star metallicity, apparent brightness and mass, to name just a few).

The two most important correlation diagrams are probably the mass-period diagram and the eccentricity-period diagram. Ideally, one would like to plot logM, logP, and e in three dimensions, but I’ve always felt that static 3D diagrams don’t work very well. I think one is best off scaling the size of the symbol to Msin(i) and going with a 2D diagram of eccentricity vs log Period. I fooled around with various scalings, and decided that a point radius proportional to Msin(i)**0.4 looks the best.

That leaves color to impart additional information. As the number of planets increases, one is increasingly better off allowing the points in correlation diagrams to be partially transparent. An opacity of 0.7 give an immediate depth of field for overlapping points, and will continue to work well on Keynote slides until there are more than a thousand planets.

The planet-metallicity correlation can be made evident by mapping the metallicity of the parent star onto the hue of the point. With a rainbow scale where red is Fe/H=-0.5 (low metallicity) and violet is Fe/H=0.5 (high metallicity) it’s immediately clear that the planets found to date are skewed toward metal rich stars.

Looks cool.

The Mathematica Hue command allows control of hue, saturation, brightness and opacity. The HSB color scheme potentially allows for quantities to be displayed simultaneously, meaning that 6D correlation diagrams are possible. Can the saturation and brightness indices be put meaningfully to work?

I think the answer is probably yes, but my sense is that it will be tough to get a full return from all three color dimensions. In the diagram below, metallicity maps to hue (as before) and the V magnitude of the parent star maps to brightness. Only hues from 0.00 to 0.70 are used, to avoid the wrap-around. Saturation is left at 1.00 for all points:

Barfy colors are now in the lead, and some extra information is imparted. The hot Jupiters (in the lower left hand corner of the diagram) are noticeably darker than the eccentric giants. This is because increasingly, the hot Jupiters are being located by transit surveys, which look at much dimmer stars than does the RV method which surveys stars that are typically in the V=5-8 range. The extra color dimension is thus giving a sense of one of the biases in the diagram — Hot Jupiters are overrepresented because they’re easier to find.

What happens when one uses all three color dimensions? In the following diagram, the degree of color saturation is mapped to the mass of the parent star. With the first scaling that I tried, there’s not a whole lot of change from the previous plot. I think, though, that with more experimentation, the color saturation can be put to use. Note, too, that the dynamic range is reduced by the up-front demand for 70% transparency.

The diagrams really benefit from higher resolution. For example, looking at the hot Jupiters, there’s an interesting zone of avoidance at the lower left hand corner. The lower-mass planets are not populating the region that contains the hottest and most circular hot Jupiters. This might stem from a fundamental composition difference, although it’s also true that Neptune-mass planets don’t turn up yet in transit surveys.

As seen on AO5
greg posted in worlds on November 13th, 2008

Last night, I noticed Venus and Jupiter hanging low and bright about ten degrees apart in the deep blue twilight. Noctilucent cirrus clouds hinted that the full Moon had just risen on the other side of the sky. No matter how intricate the detail in a radial velocity curve, no matter how fine-grained the transit ingress, there’s something undeniably tantalizing and mysterious about the direct image. There’s a certain solidity to seeing with your own eyes.

The embargo just lifted, and by now, the news of the images of the planets orbiting HR 8799 and Fomalhaut are all over the media. NYTimes, check. Washington Post, check. Fox News, check.

I was very happy to see that the media coverage of these two amazing, largely independent discoveries ended up quite fair and balanced. I had been wondering whether perhaps HR8799 would get shouldered out of the limelight. There’s definitely something to be said for steppin’ into the ring with the HST Press Machine at your back, and a cool-looking picture of a planet orbiting (of all stars!) Fomalhaut. A star with a name like a rocket.

Fomalhaut, furthermore is Magnitude 1. HR8799 checks in with B=6.198 and V=5.964. “It’s up now, in the Great Square of Pegasus, slightly too dim to see with the naked eye. But your cat’s eyes are actually sensitive enough to see it! If you’re so inclined, you can make your cat go outside tonight and share in this historic discovery.”

I think it’s quite significant that these planets have been detected around stars that are more massive than the Sun. We already know from the radial velocity surveys (and specifically the targeted surveys of John Johnson and Bunei Sato) that higher-mass Jovian planet formation was more efficient around higher-mass stars than around stars of solar mass and below. Johnson and Sato surveyed “retired” A-type stars that are now turning into red giants, and which are cool enough to have the deep lines in their spectra that the RV-detection method requires. Johnson and Sato both independently found that these stars are frequently producing planets that are more massive than Jupiter in orbital periods of several hundred days.

Sato’s detection in early 2007 of a 7.6 Jupiter-mass planet orbiting Epsilon Tauri (2.7 solar masses) in the Hyades is probably a good example of the type of planet that’s showing up in these new images, and Eps Tau b provides good support for the case that this category of objects arose from gravitational instability. The Hyades were a tough environment for planet formation via core accretion, due to the intense UV radiation that caused the disks to lose gas quickly (see this oklo post).

Remnant debris disks would be expected around young stars that had massive enough disks to trigger gravitational instability. Also, in general, the more massive the star, the more massive the disk. And finally, if the planets formed via gravitational instability, one wouldn’t expect a bias toward high metallicity. If this idea is correct, as more of these planets are imaged, there shouldn’t be a metallicity correlation with the parent star.

Bruce Macintosh was kind enough to point me to some links that his team has set up. The images and movies are well worth a visit:

Travis and Christian put together a temporary holding pen at
http://www.photospheres.us/barman/HR8799/

My personal favorites are the “real” orbital motion one
http://www.photospheres.us/barman/HR8799/Movie00-HR8799-real-orbitalmotion.mov

and the movie showing the rotational imaging technique:
http://www.photospheres.us/barman/HR8799/Movie04-HR8799-adi.mov
(left panel is raw Keck images with the image derotator off, so artifacts
are fixed while stuff on the sky rotates; middle panel is image with a
weighted-moving-average PSF subtracted; rightmost is the cumulative derotated
image.)

Also a finding chart showing HR8799 and 51 Peg.

The HR8799 family portrait, with three planets zipping around on Keplerian orbits immediately brings to mind our own outer solar system. Ironically, however, if the GI formation hypothesis is correct, we’re actually observing planetary systems that have even less kinship to our own than do systems like HD 209458b and 51 Peg that harbor hot Jupiters (which oddball as they seem, probably formed via core accretion, just like Jupiter).

Barnard 681
greg posted in worlds on November 11th, 2008

The HST photo of the photoevaporating molecular clouds of M16 is the iconic go-to image, but it’s always struck me as veering toward flash over substance. The “pillars of creation” name combines with the visual cues to create the illusion that you’re looking at something in an up-down gravitational field.

I think my favorite astronomical image is the not-quite-so-famous photo of Barnard 68. Here, one gets a far more immediate and accurate sense of what one is actually seeing. A cold, black self-gravitating cloud, looming in the foreground, blotting out the stars. It’s easy to imagine a sped-up film which depicts the cloud boiling and writhing with its internal turbulence.

There’s a certain undeniable menace to the dark cloud, and not without reason. If we rewind the tape by 4.54 billion years, all the material in our own solar system would have looked not unlike Barnard 68. If viewed in time-lapse, the pre-solar dark cloud would have collapsed from inside out upon itself, leading to the formation of the Sun, the planets, and eventually, a vanguard of five delicately engineered probes heading tentatively out into the galaxy. There would have indeed been cause for long-term concern…

Creepy undertones aside, Barnard 68 is a great slide to show during talks about star and planet formation. If the Sun is a 0.2mm grain of sand in San Francisco, Barnard 68 is half a mile across and located roughly at the distance of Los Angeles. The dark cloud itself is the equivalent of grinding up one percent of three small grains of sand, and dispersing the resulting powder through a half-mile wide volume.

The last time I gave a talk, it occurred to me that I’d never had enough faith in common sense to actually question whether that last analogy is appropriate, and indeed nobody in an audience has ever called me on it. Is it really possible to grind up 3% of a sand grain so that it creates an opaque half-mile wide cloud? That sounds totally nuts!

Asteroid 99942 Apophis (Image Source).

The absolute finest that one could envision grinding up a sand grain, while still retaining it in some sense as powdered “sand”, would be to the level of individual silica (SiO2) molecules. A 0.2 mm grain contains roughly 6×10^17 silica molecules. There’d thus be ~2×10^16 molecules available to disperse through the half-mile-wide volume of our model for Barnard 68. Scaling up to the solar mass, this would imply a Barnard 68 chock full of kilometer-wide asteroids, whereas in reality, the dust in Barnard 68 is micron-sized, roughly the consistency of cigarette smoke.

If the metals in Barnard 68 were in the form of km-wide asteroids, the cloud would indeed be transparent — fewer than one in a billion of the photons from the background stars would be absorbed on their way through the cloud.

5381
greg posted in worlds on November 3rd, 2008

Image Source.

The month of October slipped by. No new oklo posts. Like seemingly everyone else, I’ve been in a state of continual distraction regarding the election. Instead of writing posts about planets, spare moments are spent scanning the news.

Sometimes, if you’re waking up in the middle of the night, there’s perspective in the knowledge that one can build a fully to-scale model of the Earth-Sun system by taking a grain of sand and holding it two arms lengths away from a dime. A real time simulation can then be put into effect by moving the sand grain through 6.92 degrees per week.

I do have a post nearly done in draft form, but my colleague, Prof. Jonathan Fortney, eliminated any chance that I’ll get it finished and posted before Nov. 5th, by introducing me to fivethirtyeight.com. Over there, you can get the latest polling data with a 10,000-trial Monte-Carlo sheen:

root N1
greg posted in worlds on September 25th, 2008

Jason Wright recently sent me an advance copy of a preprint from his group that sums up the state of knowledge of the 27 multiple exoplanet systems that are currently known to orbit ordinary stars. It’s really quite remarkable, in scanning through the table of planets, how alien the systems are, how, on the whole, they are so unlike the solar system.

We’re fast approaching the tenth anniversary of the discovery of the three planets orbiting Upsilon Andromedae. I vividly remember setting up integrations of the outer two orbits in that system just after it was announced, and watching the eccentricities of planets “c” and “d” cycle through their huge (compared to solar system) variations. At that time, I had never bothered to give secular theory the slightest consideration (aww, that stuff was all worked out in the 18th century). It was a revelation to watch the orbits shimmer and vibrate as the integrator ticked off the centuries at the rate of a million years an hour.

As the multiple-planet business enters its second decade, emphasis is shifting toward the detection of systems with ever-lower planet masses. Ups And packs at least two thousand Earth masses into the inner several AU surrounding the star. HD 40307, by contrast has planets that start at only four times the mass of Earth.

As the planetary masses go down, so to do the signal strengths. The Upsilon Andromedae periodogram practically wears its planets on its sleeve, whereas nowadays, the surveys are likely combing though forests of tantalizing yet ambiguous peaks. Detectability increases with the square root of the number of observations, which exerts pressure to spend more telescope time on fewer stars.

From the standpoint of someone who’s interested in planet-planet dynamics, systems like Gliese 876, with its incredible signal-to-noise are clearly the most valuable. From the perspective of someone who’s interested in planet formation and the statistics of the galactic census, the systems with low-mass planets are a bigger deal. A single statistic that captures the relative value of a multiple-planet system could be expressed as:

Where the sum inside the root is over the planets in the system, and the quantities are the planetary masses, M, the rms of the residuals to the fit, $\sigma$, and the radial velocity half-amplitudes, K. The statistic seems to do a reasonable job of aggregating signal-to-noise and the potential for dynamical interaction, while simultaneously placing emphasis on lower mass planets. Plugging in the numbers, the known multiple-planet systems stack up with the following ranking:

Interestingly, the ranking seems to capture the vagaries of the press release industry pretty well. The top six multiple planet systems have all seen their names appear in the New York Times, in some cases on the front page:

HD 40307:

Gliese 581:

Gliese 876:

HD 69830:

Mu Arae:

55 Cancri:

Newsworthiness appears to run out, however, when the list reaches the two-planet system orbiting HD 190360:

Amazon, however, has kindly sponsored a link that puts it up for sale:

Now that flipping houses is passé…

New Horizons0
greg posted in worlds on September 6th, 2008

Image Source.

Last May, Mark Marley sent me a link to the photograph shown above. It’s a Cassini image of Alpha Centauri A and B hanging just above the limb of Saturn. It provides an interesting bookend to the remarkable pictures that can be taken from Earth when Saturn and the Moon are close together in the sky. Mystery on the scientific horizon of the year 1610 has transformed itself into mystery on the horizons of today.

Image source.

It’s also a nice coincidence that the actual distance between the two components of Alpha Cen is similar to the distance between Earth and Saturn. Right now, Alpha Cen A and B are more than 20 AU apart, but within our lifetimes, they’ll close to nearly the Earth-Saturn distance as they reach the next periastron of their 80-year orbit in May 2035.

We’re fortunate that we’ve arrived on the scene as a technological society right at the moment when a stellar system as interesting as Alpha Cen is in the very near vicinity. During the last interglacial period, Alpha Cen did not rank among the brightest stars in the sky. A hundred thousand years from now, the Alpha Cen stars will no longer be among our very nearest stellar neighbors, and in a million years, they will have long since faded from naked-eye visibility. At the moment, though, Alpha Centauri is drawing nearer at 25 km/sec, a clip similar to the Earth’s orbital velocity around the Sun. It’s as if we’re on the free trial period of an interstellar mission…

And what of the status of the observational search? In the interim since the last oklo.org update, Debra Fischer obtained one year of NSF funding to begin high-cadence radial velocity observations of the Alpha Cen system with the CTIO 1.5m telescope in Chile. Debra, along with Javiera and a number of CTIO scientists have worked very hard to get the telescope and a spectrograph into condition for high-precision Doppler work. Many nights of Alpha Cen observations have now actually been carried out, and by all indications, the prospects look quite promising from an instrumental standpoint. The project will need long-term funding, though, since it will take of order 3-5 years of dedicated observation to reach any truly habitable worlds that are orbiting our nearest stellar neighbors.

De revolutionibus0
greg posted in worlds on September 1st, 2008

In preparing my talk for the Torun meeting, it seemed appropriate to take a careful look at the book that got the whole planetary systems business going — De revolutionibus orbium coelestium (On the Revolutions of Heavenly Spheres) by Copernicus.

Being not in possession of a classical education, that meant settling for an English translation, but it’s interesting to look at the original Latin editions (which are dramatically out of copyright, and hence available from the ether in the departure lounge at O’Hare if one is willing to fork out for a wi-fi connection). Here’s the frontispiece of Harvard’s edition:

The text translates to:

Diligent reader, in this work, which has just been created and published, you have the motions of the fixed stars and planets, as these motions have been reconstituted on the basis of ancient as well as recent observations, and have moreover been embellished by new and marvelous hypotheses. You also have most convenient tables from which you will be able to compute those motions with the utmost care for any time whatever. Therefore, buy, read and enjoy.

To a modern sensibility, the exhortation to buy the book seems to run at cross purposes with the warning just below (written in Greek for heightened effect):

Let no one untrained in geometry enter here.

Certainly, in trying to make sense of the text, it’s clear that the warning is no empty threat. The book, with its arduous descriptions of ephemerides is tough going. Section 17 of Book V presents a typical example:

Now it was made clear above that in the last of Ptolemy’s three observations Mars, by its mean movement as at 244.5 deg, and its anomaly of parallax was at 171 deg, 26′. Accordingly during the year between there was a movement of 5 deg 38′ besides the complete revolutions. Now for the 2nd year of Antoninus on the 12th day of Epiphi the 11 month by the Egyptian calendar 9 hours after mid-day, i.e. 3 equatorial hours before the following midnight, with respect to the Cracow meridian, to the year of Our Lord 1523 on the 8th day before the Kalends of March 7 hours before noon, there were 1384 Egyptian years 251 days 19 minutes [of a day]. During that time there were by the above calculation 5 deg 38′ and 648 complete revolutions of anomaly of parallax. Now the regular movement of the sun was held to be 257 1/2 deg. The subtraction from 257 1/2 deg of the 5 deg 38′ of the movement of parallax leaves 251 deg 52′ as the mean movement of Mars in longitude. And all that agrees approximately with what was set down just now.

By connecting observations from the Ptolemaic era with his own (and other contemporary) observations, Copernicus was able to achieve a great improvement in timing accuracy. Remarkably, his combination of timing data and positional measurements for solar system planets such as Mars give a signal-to-noise quite similar to the modern data that we currently have for transiting hot Jupiters such as HD 149026b. These extrasolar planets have been observed over hundreds of orbits with both ground-based photometry (for timing) and with radial velocities (for elucidating the orbital figure).

Given that the distances to the planet-bearing stars are millions of times larger than the distances to the solar system planets, this is a testament both to how far we’ve come in 500 years, and simultaneously, to the durability of the Copernican accomplishment.

The naming of Names5
greg posted in worlds on August 10th, 2008

Sometimes, when I give a talk, I’m asked why the extrasolar planets don’t have evocative names.

Names and labels carry a heavy freight and they get people worked up. The agonized IAU deliberations vis-à-vis Pluto’s status as a plutoid or a planet or a dwarf planet constituted by far the biggest planet news of 2006, dwarfing, for example, the discovery of the triple Neptune system orbiting HD 69830. It’s unlikely that New Horizons would have gotten its congressional travel papers in order had Pluto been a plutoid right from the start.

When new comets and asteroids are discovered, their names generally follow on fairly quickly. Comets are bestowed with the name of the discoverer(s), and as a result, Dr. Hale and Mr. Bopp are entwined together in immortality. With asteroids, the discoverer gets the naming rights (subject to certain IAU rules), resulting in both some cool choices, (99942) Apophis, (3040) Kozai, as well as a Kilroy-was-here sloop of John B’s: (6830) Johnbackus, (20307) Johnbarnes, (4525) Johnbauer, (15461) Johnbird, (12140) Johnbolton, (16901) Johnbrooks, (11652) Johnbrownlee, (26891) Johnbutler, etc. etc.

Galileo, in sighting the moons of Jupiter, made the first telescopic discovery of solar system objects. Ever on the eye for an angle, he tried to increase his odds of patronage by naming his new moons “The Medicean Stars” in reference to Cosimo II de’ Medici, fourth Grand Duke of Tuscany. It’s now generally agreed that Mr. Medici, whatever his merits, was rather dramatically undeserving of the following accolades:

Serenissimo Grand Duke, “scarcely have the immortal graces of your soul begun to shine forth on earth than bright stars offer themselves in the heavens, which, like tongues [longer lived than poets] will speak of and celebrate your most excellent virtues for all time.”

Later in the seventeenth century, when Giovanni Cassini discovered Saturn VIII, V, III, and IV, he tried the same tactic. Three hundred and twenty two years later, his prose reads like a purple toad:

In the Conclusion, the Discoverer considers that the Antient Astronomers, having translated the Names of their Heroes among the Starrs, those Names have continued down to us unchanged, notwithstanding the endeavour of following Ages to alter them; and that Galileo, after their Example, had honoured the House of the Medici with the discovery of the Satellites of Jupiter, made by him under the Protection of Cosmus II; which Starrs will be always known by the Name of Sidera Medicea. Wherefore he concludes that the Satellites of Saturn, being much more exalted and more difficult to discover, are not unworthy to bear the Name of Louis le Grand, under whose Reign and in whose Observatory the same have been detected, which therefore he calls Sidera Lodoicea, not doubting but to have perpetuated the Name of that King, by a Monument much more lasting than those of Brass and Marble, which shall be erected to his Memory. [1]

In order to forestall just these sorts of embarrassments, the current IAU naming convention specifies that, the names of individuals or events principally known for political or military activities are unsuitable until 100 years after the death of the individual or the occurrence of the event.

The Medicean Stars are neither medicean nor stars, and so it’s not surprising that the name failed to stick. In 1847, the names of the Sidera Lodoicea were finally standardized to Iapetus, Rhea, Tethys, and Dione, all of which just sound right. It’s remarkable that nearly two hundred years elapsed before the final names were assigned.

At present, there’s no IAU sanction for naming extrasolar planets. Sometimes astronomers give it a go anyway, as seen here in the abstract for astro-ph/0312382:

Three transits of the planet orbiting the solar type star HD209458 were observed in the far UV at the wavelength of the HI Ly-alpha line. The planet size at this wavelength is equal to 4.3 R_Jup, i.e. larger than the planet Roche radius (3.6 R_Jup). Absorbing hydrogen atoms were found to be blueshifted by up to -130 km/s, exceeding the planet escape velocity. This implies that hydrogen atoms are escaping this “hot Jupiter” planet. An escape flux of >~ 10^10g/s is needed to explain the observations. Taking into account the tidal forces and the temperature rise expected in the upper atmosphere, theoretical evaluations are in good agreement with the observed rate. Lifetime of planets closer to their star could be shorter than stellar lifetimes suggesting that this evaporating phenomenon may explain the lack of planets with very short orbital distance.

This evaporating planet could be represented by the Egyptian God “Osiris” cut into pieces and having lost one of them. This would give us a much easier way to name that planet and replace the unpleasant “HD209458b” name used so far.

The name Osiris doesn’t seem to have caught on, perhaps because (5×10^9)(3.17×10^7)(1×10^10) is a good deal less than (1.4×10^30). Also, I’d tend to disagree that HD 209458b is “unpleasant”. A sequence of letters and numbers carries no preconception, underscoring the fact that these worlds are distant, alien, and almost wholly unknown — K2 is colder and more inaccessible than Mt. McKinley, Vinson Massif or Everest.

Ray Bradbury, in several of his stories, tapped into the profound significance of names. In the 2035-2036 section of The Martian Chronicles, he wrote:

The old Martian names were names of water and air and hills. They were the names of snows that emptied south in the stone canals to fill the empty seas. And the names of sealed and buried sorcerers and towers and obelisks. And the rockets struck at the names like hammers, breaking away the marble into shale, shattering the crockery milestones that named the old towns, in the rubble of which great pylons were plunged with new names: Iron Town, Steel Town, Aluminum City, Electric Village, Corn Town, Grain Villa, Detroit II, all the mechanical names and the metal names from Earth.

I think we’ll eventually reach the extrasolar planets, and in so doing, we’ll find out what their true names are.

Molybdenum1
greg posted in worlds on June 29th, 2008

Download 1017 x 761 px version here.

This dry range is near Gabbs, Nevada.

I remember stopping at a bar in Gabbs on a Saturday night in October 1993. We were low on gas, having foolishly skipped a possibility to fill up at Walker Lake. We’d been driving all day. In the deserted gravel lot, the sky was freezing black and spangled with stars.

I drank a beer and talked to the only other patron — a grizzled Vietnam veteran who worked at the molybdenum mine. The word molybdenum sounded strange, exotic. In 1993, the price of molybdenum was in free fall, and in 1994, it would reach a low of $3,510 per metric ton ($1.59 per pound). The mine was laying off workers and was in danger of closing.

The gas station in Gabbs was closed. The bartender called the nearest possibility, the old Pony Express station Middlegate, 50 miles north. “You’re in luck, they’ve got gas.”

The current spot price for Molybdenum oxide is 33.50 dollars per pound, a less-noticed example from the many changes that make 1993 seem increasingly a part of a bygone millennium. Hundreds of extrasolar planets, e-mail inboxes that routinely receive hundreds of messages (mostly spam) per day, and this uneasily growing realization that the raw materials may be the deciding factor after all.

I wonder whether the extrasolar planets will ever have a flatly practical economic value. The scramble to detect new planets often feels like a land rush, but is there a real possibility that we’ll eventually pack up and go to these systems that are showing up in the correlation diagrams? Do the economics of interstellar travel ever work out?

In this context, it’s slightly disconcerting to remember that the molybdenum has already made the interstellar journey (see e.g. here). The most abundant Mo isotope is molybdenum-98, which constitutes 24.14% of Earth’s molybdenum. These atoms were produced both via the s-process, which takes place in red giant stars, and where a chain of slow neutron captures is interspersed with beta decays, and by the r-process, which occurs in supernovae.

The fact that the resources made the trip for free makes it seem a little more likely that we may well be able to get more, but only if we pay…

in situ?4
greg posted in worlds on June 17th, 2008

Man! Like everyone else over the past 24 hours, I’ve been thinking about that new crop of Superearths.

The conventional wisdom (over which I was waxing enthusiastic a mere 36 hours ago) holds that Mayor’s new population of planets are essentially failed giant planet cores which began forming at considerably larger radii in the protostellar disk and then experienced significant inward migration as they built themselves up. In this scenario, the Superearths arise from more or less the same sort of process (but with a different outcome) that formed the giant planets in our own solar system.

What’s struck me, however, is the odd resemblance between a multiple-planet system like HD 40307 and the regular satellite systems of the Jovian planets. In both cases, the characteristic orbital period is of order a week, and the system mass ratio (satellites-to-central-body) is of order 2 parts in 10,000.

In the Ward-Canup theory, the regular satellites of the Jovian planets are thought to have formed more or less in situ in gas-starved disks (see here for more discussion). If the new population of planets is somehow the result of an analogous formation process, then they really will be superEarths, as opposed to subNeptunes, and as a consequence, their transit depths will be small.

Disks2
greg posted in worlds on April 21st, 2008

A few nights ago, we were looking at the skies through a 10-inch telescope set up in our backyard. The neighbor’s security light made a mockery of any pretense of dark-sky observering, but nevertheless, there’s something remarkable about stepping outside and having your retina absorb light that’s been on the wing for 10 million years.

Using averted vision, I could just make out M81 and M82. They look like this:

On the Astronomy Picture of the Day, one sees a lot more detail:

With the aid of lurid false color, the sense of galactic catastrophe is unmistakable. M82, in particular, emanating distended neon-red lightning bolts, looks positively unwell. The two galaxies, of course, are in the process of merging, and over the next billion years, will convert their delicate dynamical structures into the frenzied agglomeration of orbits that constitutes an elliptical galaxy.

But I like the fact that through the telescope, it’s just two faint misty patches. Static. Unhurried. Completely calm. A billion years is an incredibly long time. The view gives a good illustration of Eisenhower’s remark that “the urgent is seldom important and the important is seldom urgent.”

Saturn, too, was high in the sky, and looked like this.

After seeing M81 in the Miocene, it’s slightly jarring to note that the light from Saturn had left the planet after dinner while I was doing the dishes.

With the low-power telescope view, it’s easy to see why Galileo was puzzled when he first saw Saturn under magnification. Huygens’ accomplishment in figuring out the true geometry of an inclined planet with rings suddenly seems much more impressive. And now, there’s spacecraft all the way out there, sending photo after incredible photo back to the Deep Space Network. I was very happy to hear that Cassini’s first mission extension was approved.

Image Source.

M81 and the rings of Saturn are separated by an enormous expanse of scale and time, but they are both excellent examples of disks whose detailed structures are created by a combination of external forces and self-gravity. The protostellar disk that gave rise to the solar system falls in this same category of object.

An important issue in the study of protostellar disks is the identification of when a disk is massive enough to experience the development of spiral instabilities. Stefano (in addition to all the work he’s been doing on the systemic project) has been doing a detailed study of this problem. He’s found that the presence of a gap in a self-gravitating disk makes the disk far more prone to spiral instabilities than it would otherwise be. Gaps are unavoidable if a massive planet is forming in the disk. The spiral instabilities generate mass and angular momentum transport that efficiently attempt to fill in the gap. This new phenomenon has potentially very important ramifications for our understanding of giant planet formation and protostellar disk evolution.

Stefano’s paper has been accepted for publication in the Astrophysical Journal Letters, and will be appearing on astro-ph very shortly. In the meantime, here’s an advance copy in .pdf format.

Also, be sure to check out the website that Stefano has set up to explain this research. He has some very cool animations of protostellar disks succumbing to catastrophic instabilities, and he provides a link to the slides for his recent FLASH seminar on his work. My personal favorite is the graphical rendering of the solution to the thorny integro-differential equation that has to be solved to determine the growth rates, the pattern speeds and the overall appearances of the unstable spiral modes:

It won’t last forever…10
greg posted in worlds on April 14th, 2008

In a nutshell, here’s the question: “What are the odds that the planets will experience a dramatic orbital instability before the Sun turns into a red giant and destroys the Earth?”

In a nutshell, here’s the answer: “About 1%.”

I’m very happy that it’s now possible to write a full follow-up report on last summer’s post about UCSC physics undergraduate Konstantin Batygin’s work on the long-term stability of the solar system.

Recapping last summer’s post:

The long-term stability of the planetary orbits has been a marquee-level question in astronomy for more than three centuries. Newton saw the ordered structure of the solar system as proof positive of a benign deity. In the late 1700s, the apparent clockwork regularity of interaction between Jupiter and Saturn helped to establish the long-standing concept of Laplacian determinism. In the late Nineteenth Century, Poincaré’s work on orbital dynamics provided the first major results in the study of chaotic systems and nonlinear dynamics, and began the tilt of the scientific worldview away from determinism and toward a probabalistic interpretation.

In recent years, it’s become fairly clear that the Solar System is dynamically unstable in the sense that if one waits long enough (and ignores drastic overall changes such as those wrought by the Sun’s evolution or by brushes with passing stars) the planets will eventually find themselves on crossing orbits, leading to close encounters, ejections and collisions.

Desktop PCs are now fast enough to integrate the eight planets into the future for time scales that exceed the Sun’s hydrogen burning lifetime. This makes it possible to explore future dynamical trajectories for the solar system. Over the long term, of course, the planetary orbits are chaotic, and so for durations longer than ~50 million years into the future, it becomes impossible to make a deterministic prediction for exactly where the planets will be. The butterfly effect implies that we can have no idea whether January 1, 100,000,000 AD will occur in the winter or in the summer. We can’t even say with complete certainty that Earth will be orbiting the Sun at all on that date.

We can, however, carry out numerical integrations of the planetary motions. If the integration is done to sufficient numerical accuracy, and starts with the current orbital configuration of the planets, then we have a possible future trajectory for the solar system. An ensemble of integrations, in which each instance is carried out with an unobservably tiny perturbation to the initial conditions, can give a statistical indication of the distribution of possible long-term outcomes.

Here’s a time series showing the variation in Earth’s eccentricity during a 20 billion year integration that Konstantin carried out. In this simulation, the Earth experiences a seemingly endless series of secular variations between e=0 and e=0.07 (with a very slight change in behavior at a time about 10 billion years from now). The boring, mildly chaotic variations in Earth’s orbit are mostly dictated by interactions with Venus:

Mercury, on the other hand, is quite a bit more high-strung:

These two plots suggest that the Solar System is “good to go” for the foreseeable future. Indeed, an analysis (published in Science in 1999) by Norm Murray and Matt Holman suggests that the four outer planets have a dynamical lifetime of order one hundred quadrillion years (ignoring, of course, effects of passing stars and the Sun’s evolution).

Work by Jacques Laskar, on the other hand, who is Laplace’s dynamical heir at the Bureau des Longitudes in Paris, suggests that the inner solar system might be on far less stable footing.

Laskar performed the following experiment (described in this 1996 paper, which is well worth reading). Using an extremely fast (but approximate) numerical code which incorporates more than 50,000 secular perturbation terms involving the eight planets, Laskar integrated the current configuration of the Solar System 2 billion years into negative time. He then made four “realizations” of the solar system in which Earth’s position was shifted by a mere 150 meters in different directions. These four nearly identical variations of the Solar System were each integrated backward in time for a further 500 million years. Due to the highly chaotic nature of the system, each of Laskar’s four simulations spent most of the computational time exploring entirely different dynamical paths within the Solar System’s allowed phase space.

When the four integrations were complete, Laskar examined the individual orbital histories and selected the trajectory in which Mercury’s eccentricity achieved its largest value. The Solar system configuration at the time of this greatest eccentricity excursion was then used as a starting condition for a second set of four individual 500-million year integrations. At the end of this second round of calculations a new set of starting conditions was determined by again selecting the configuration at which Mercury’s excursion was the largest.

Here’s a diagram that flowcharts (using positive time) the basic idea underlying Laskar’s bifurcation method:

After 18 rounds, which when pieced together yielded a 6 billion year integration, Laskar observed that Mercury’s eccentricity had increased to e>0.5. Mercury, and indeed the entire inner solar system, had gotten itself into extremely serious trouble. A secular integration scheme can’t handle close encounters, though, and so the final gory details were left to the imagination. Nevertheless, it was clear that by the end of Laskar’s simulation, Mercury was in line to suffer a close encounter with Venus, or a collision with the Sun, or an ejection from the Solar System. The 1996 Laskar integration was the first explicit demonstration of the Solar System’s long-term dynamical instability. In essence, it brought a 300-year quest to a dramatic head.

I read Laskar’s paper in 1999, shortly after the discovery of the Upsilon Andromedae planetary system spurred me into a crash-course study of orbital dynamics. His calculations seemed to raise some really interesting questions. What is the dynamical mechanism that destabilized the inner Solar System? Was the elevation of Mercury’s eccentricity a consequence of the secular perturbation approach that he applied? Would his bifurcation strategy find a similar result when used with direct numerical integration of the equations of motion?

Two years ago, I told Konstantin about Laskar’s experiment, and we decided to see if we could answer the questions that it raised. As a first step, Konstantin set about replicating Laskar’s simulation strategy with full numerical integrations. All told, this required over a year of computing, including a lot of effort to make sure that the buildup of numerical error was kept under control.

Our version of Laskar’s method works as follows (and is shown in the flow chart above). First, a direct integration spanning 500 million years, ~100 Earth Lyapunov times, is made using the current Solar System configuration as a starting point. Picking up at the integration’s endpoint, five solutions for 500 million years are computed. Four of these use initial conditions in which Earth’s position is shifted, while one uses the unaltered solution. Because initial uncertainties diverge exponentially with time, a shift of 150 meters in Earth’s position 500 million years from now corresponds to an initial error today of order 10^-42 meters — ten orders of magnitude smaller than the Planck scale. After the five bifurcated trajectories are computed, the solution in which Mercury attains the its highest eccentricity is preserved to the nearest whole million years, and five new trajectories are started.

Much to our amazement, the bifurcation strategy is capable of showing Mercury the door in a hurry. In our first complete experiment, only three Laskar steps were required in order to coax Mercury into a collision with Venus at a time 861.455 million years from now:

And it wasn’t only Mercury that ran into problems. At t=822 million years, shortly after Mercury’s entrance into a zone of severe chaos, Mars — rovers and all — was summarily ejected from the Solar System:

This is some pretty heavy stuff. We have a direct numerical solution of Newton’s equations in which the solar system goes unstable well before life on Earth is expected to perish. (Can GR save the day? Read the paper.)

So what’s the mechanism that causes the instability?

At first, we thought that the dynamics were stemming from an overlap of mean motion resonances, but we were able to show that isn’t the case. In the end, Konstantin used the technique of synthetic secular perturbation theory to demonstrate that the culprit is a linear secular resonance with Jupiter. In short, Mercury winds up in a situation where the resonant argument (omega_1 - omega_5) librates between +19.8 and -43.56 degrees for three million years. The result is a steady increase in Mercury’s eccentricity to a dangerously high value:

The evolution of Mercury’s orbit is driven both directly by Jupiter, and to a greater extent by Jupiter’s influence transmitted through Venus. It’s an amazing, scary possibility, and the full details are in the paper.

Needless to say, we were thrilled when the full picture came together. We wrote up our work and submitted it to the Astrophysical Journal in mid-January. I got in touch with the UCSC public affairs office with an eye toward issuing a press release once our paper cleared the refereeing process.

Then, to our total astonishment and dismay, we were scooped! It turns out that Jacques Laskar himself has also been working on the problem. On February 22nd, he posted an astro-ph preprint of a paper that will be appearing in Icarus. He beat us to the punch with a basic result that’s fully in line with what we found. Here’s his astro-ph abstract:

A statistical analysis is performed over more than 1001 different integrations of the secular equations of the Solar system over 5 Gyr. With this secular system, the probability of the eccentricity of Mercury to reach 0.6 in 5 Gyr is about 1 to 2 %. In order to compare with (Ito and Tanikawa, 2002), we have performed the same analysis without general relativity, and obtained even more orbits of large eccentricity for Mercury. We have performed as well a direct integration of the planetary orbits, without averaging, for a dynamical model that do not include the Moon or general relativity with 10 very close initial conditions over 3 Gyr. The statistics obtained with this reduced set are comparable to the statistics of the secular equations, and in particular we obtain two trajectories for which the eccentricity of Mercury increases beyond 0.8 in less than 1.3 Gyr and 2.8 Gyr respectively. These strong instabilities in the orbital motion of Mecury results from secular resonance beween the perihelion of Jupiter and Mercury that are facilitated by the absence of general relativity. The statistical analysis of the 1001 orbits of the secular equations also provides probability density functions (PDF) for the eccentricity and inclination of the terrestrial planets.

Rather ironically, Laskar did not use his bifurcation method to solve the problem. By sticking with his secular code, he’s able to get a big speedup over direct numerical integration, which allowed him to perform a suite of 1001 straight-line integrations of the secular equations. The resulting statistics of these allow him to place a 1-2% probability of Mercury going haywire within 5 billion years. (With general relativity included, this number is probably closer to 1%, although his integrations in the GR case haven’t finished yet.)

So sadly, no UCSC press release will be forthcoming. Priority of discovery goes to the Bureau of Longitudes, and our paper, which will be appearing in the Astrophysical Journal, will be providing dramatic confirmation of the mechanism by which the Solar System can come undone.

Our paper (Batygin, K. & Laughlin, G. 2008, Astrophysical Journal, In Press.) is available on astro-ph.

Hawaii1
greg posted in worlds on March 11th, 2008

Image Source.

Over the past two days, I got the opportunity to fly to Hawaii to give two talks for the Keck Observatory’s Evening With Astronomers series. The talks focused on extrasolar planets (here’s a link to the slides in Quicktime format, ~40MB , along with the audio files of (1) a planetary system in a 2:1 resonance, (2) an unstable planetary system, and (3) another unstable system). Both talks were on Kona coast of the Big Island, where, behind the palm trees, Mauna Kea looms up 13,796 feet in the hazy volcanic distance.

The landscape here resembles nothing so much as a habitable, terraformed Mars. Hardened ropes of lava run down to the water’s edge:

In the pre-dawn light this morning, the air was totally silent, and it was easy to imagine that I was actually on Mars, before the water was gone, when a Northern hemispheric ocean lapped up against the lava of the lowermost slopes of Elysium Mons:

Image Source.

In the last few years the Martian landscape has become much more familiar, as the Spirit and Opportunity rovers crawl across the surface and radio home their photographs:

At Kona, looking out toward the lava fields, the view is positively Martian, with the most immediate difference being a sky that is a hazy blue-white rather than a hazy salmon-white. Here, the Ala Loa trail recedes into the jagged distance of what could easily be Mars:

On Mars, however, one generally has a fairly reasonable sense of what the 360-degree panorama will look like even if only part of the horizon is in view. On Earth, the situation can be quite different. Here’s the view that one gets simply by turning and looking in the opposite direction down the Ala Loa trail:

(On a marginally related note, our Alpha Centauri ApJ paper is starting to pick up some news coverage. Here’s a link to a story by National Geographic News.)

And four point five billion years later…2
greg posted in worlds on March 4th, 2008

Image Source.

The last mile of the San Lorenzo river in Santa Cruz is strongly affected by the twice-daily ebb and flow of the tides.

It’s always startling to see the tidal bore, a solitary breaking wave that runs upstream at a ~8 minute per mile pace when the tide is coming in. The San Lorenzo bore is small, usually six to nine inches high, but dramatic nonetheless. In its wake, there’s a turbulent froth of whitewater, whose eddies eventually cascade into viscous dissipation, turning the kinetic energy of organized flow into a slight heating of the water. As the Moon recedes, the Earth spins down, and the bore expends itself in a swirl of eddies.

The energy that powers the bore was all imparted during the Moon-forming impact, in which a Mars-sized object collided with Earth, leaving the planet violently shaken and stirred and spinning crazily through days that were originally just a few hours long. Now, 4.5 billion years later, the bore running up the river is a distant echo of the impact that was large enough to cause Earth to glow with the temperature of a red dwarf star.

Adapted from: Source.

There’s a nice discussion of tidal bores in the 1899 popular-level book The Tides and Kindred Phenomena in the Solar System, by Sir G. H. Darwin (son of the naturalist). The book in its entirety can be downloaded from The Internet Archive.

The Moon-forming impact, which occurred somewhere between 10 and 100 million years after the collapse of the pre-solar molecular cloud core, essentially marked the end of terrestrial planet formation in our own solar system. From a dynamical standpoint, a system undergoes a lot of evolution during a time scale of 100 million orbits. By contrast, the Milky Way galaxy is only about 40 orbits old, and is still in an effectively pristine, dynamically unrelaxed configuration.

At Darwin’s time, the first photographs of spiral galaxies were appearing, and there’s a remarkably good photo of the Andromedae galaxy on page 339 of the book:

Darwin writes:

There is good reason for believing that the Nebular Hypothesis presents a true statement in outline of the origin of the solar system, and of the planetary subsystems, because photographs of nebulae have been taken recently in which we can almost see the process in action. Figure 40 is a reproduction of a remarkable photograph by Dr. Isaac Roberts of the great nebula in the constellation of Andromeda. In it we may see the lenticular nebula with its central condensation, the annulation of the outer portions, and even the condensations in the rings which will doubtless at some time form planets. This system is built on a colossal scale, compared with which our solar system is utterly insignificant. Other nebulae show the same thing, and although they are less striking we derive from them good grounds for accepting this theory of evolution as substantially true.

In 1899, the extragalactic distance scale hadn’t been established, and so Darwin thought that M31 was a lot closer than it actually is. In dynamical terms, he would have guessed that it’s many thousands of orbits old rather than only a few dozen. Nevertheless, it’s interesting to think about what will happen to an isolated spiral galaxy by the time it’s 10^18 years old…

Toward Alpha Cen B b24
greg posted in exoplanet detection, worlds on February 24th, 2008

Image Source.

Yesterday, I gave a talk at the JPL Exoplanet Science and Technology Fair, a one-day meeting that showcased the remarkably broad variety of extrasolar planet-related research being carried out at JPL. In keeping with the wide array of projects, the agenda was fast-paced and completely diverse, with talks on theory, observation, instrumentation, and mission planning.

The moment I walked into the auditorium, I was struck by the out-there title on one of the posters: The Ultimate Project: 500 Years Until Phase E, from Sven Grenander and Steve Kilston. Their poster (pdf version here) gives a thumbnail sketch of how a bona-fide journey to a nearby habitable planet might be accomplished. The audacious basic stats include: 1 million travelers, 100 million ton vessel, USD 50 trillion, and a launch date of 2500 CE.

Fifty trillion dollars, which is roughly equivalent to one year of the World GDP, seems surprisingly, perhaps even alarmingly cheap. The Ultimate Project has a website, and for always-current perspective on interstellar travel, it pays to read Paul Gilster’s Centauri Dreams weblog.

Interest in interstellar travel would ramp up if a truly Earth-like world were discovered around one of the Sun’s nearest stellar neighbors. Alpha Centauri, 4.36 light years distant, has the unique allure. Last year, I wrote a series of posts [1, 2, 3, 4] that explored the possibility that a habitable world might be orbiting Alpha Centauri B. In short, the current best-guess theory for planet formation predicts that there should be terrestrial planets orbiting both stars in the Alpha Cen binary. In the absence of non-gaussian stellar radial velocity noise sources, these planets would be straightforward to detect with a dedicated telescope capable of 3 m/s velocity precision.

Over the past year, we’ve done a detailed study that fleshes out the ideas in those original oklo posts. The work was led by UCSC graduate student Javiera Guedes and includes Eugenio, Erica Davis, myself, Elisa Quintana and Debra Fischer as co-authors. We’ve just had a paper accepted by the Astrophysical Journal that describes the research. Javiera will be posting the article to astro-ph in the next day or so, but in the meantime, here is a .pdf version.

Here’s a diagram that shows the sorts of planetary systems one should expect around Alpha Cen B. The higher metallicity of the star in comparison to the Sun leads to terrestrial planets that are somewhat more massive.

We’re envisioning an all-out Doppler RV campaign on the Alpha Cen System. If the stars present gaussian noise, then with 3 m/s, one can expect a very strong detection after collecting data for five years:

Here’s a link to an animation on Javiera’s project website which shows how a habitable planet can literally jump out of the periodogram.

I think the planets are there. The main question in my opinion is whether the stellar noise spectrum is sufficiently Gaussian. It’s worth a try to have a look…

two for one deals?5
greg posted in worlds on February 12th, 2008

Image Source.

The Gliese 876 system is remarkable for a number of reasons. It makes a mockery of the notion that the minimum-mass solar nebula has a universal validity. It harbors one of the lowest-mass extrasolar planets known (discovered by our own Eugenio Rivera). And of course, the outer two planets are famously caught in a 2:1 mean motion resonance, in which the inner 0.8 Jupiter-mass planet makes (on average) exactly two trips around the red dwarf for every one trip made by the outer 2.5 Jupiter-mass planet.

As users of the console know, the planet-planet interactions between the Gliese 876 planets are strong enough so that one needs a self-consistent dynamical fit to the system. Even on the timescale of a single outer planet orbit, the failure of the Keplerian model can be seen on a 450-pixel wide .gif image:

The following three frames are from a time-lapse .mpg animation of the Gliese 876 system over a period of roughly one hundred years:

Each frame strobes the orbital motion of the planets at 50 equally spaced intervals which subdivide the P~60 day period of the outer planet. Upon watching the movie, it’s clear that the apsidal lines of the outer two planets are swinging back and forth like a pendulum. This oscillation has an amplitude (or libration width) of 29 degrees, and acts like a fingerprint identifier of the Gliese 876 system.

The derangement of the orbits is reflected in their continual inability to maintain an exact 2:1 orbital commensurability. The first figure up above shows that when planet c has finished exactly two orbits, it has already managed to lap planet b, which was still dawdling down Boardwalk prior to passing GO.

Planet b, however, doesn’t always run slow. The gravitational perturbations between the two planets provide a second pendulum-like restoring action which prevents the bodies from straying from the average period ratio of 2:1, which, over the long term, is maintained exactly. The degree to which the orbits themselves librate, combined with the planets’ abilities to run either ahead or behind exact commensurability is captured by the resonant arguments of the configuration. These can be defined as,

where the lambdas are mean longitudes and the curly pi’s are the longitudes of periastron. The two resonant arguments capture the simultaneous libration of the mean motions and the apsidal lines. The smaller the arguments, the more tightly the system is in resonance.

In the Gliese 876 system, the resonant arguments are both librating with amplitudes of less than 30 degrees. This is evidence that a dissipative mechanism was at work during the formation of the system. Interestingly, however, when one looks at the other extrasolar planetary systems that are thought to be in 2:1 resonance, one finds that the libration amplitudes in every case are much larger. In fact, in the HD 73526 system and in the HD 128311 system, only one of the arguments is librating, while the other is circulating. In this state of affairs, the apsidal lines act like a pendulum that is swinging over the top. In addition, the orbital eccentricites are higher, and the sum of planet-planet activity is strikingly greater (see this animation of the evolution of the HD 128311 system).

A gas disk seems to be the most likely mechanism for pushing a planetary system into mean-motion resonance. Protoplanetary disks are likely, however to experience turbulent density fluctuations. These density fluctuations lead to stochastic gravitational torques, which provide a steady source of orbital perturbations to any planets that are embedded in a disk. For a reasonable spectrum of turbulent fluctuations, it turns out that it’s rather difficult to wind up with a planetary system that is as deeply in resonance as Gliese 876. The conclusion, then, is that Gliese 876-like configurations should be quite rare. Indeed, 2:1 resonances of every stripe should constitute only a minor fraction of planetary systems, and the majority that do exist should either large libration widths or only a single argument in resonance.

If you’re interested in more detail, we’ve submitted a paper that goes into much more detail (Adams, Laughlin & Bloch, ApJ, 2008 Submitted).

Messenger4
greg posted in worlds on January 20th, 2008

Image Source.

Messenger flew by Mercury last week, and photographed vast swaths of terrain that, until now, had never been seen. The new landscapes, as expected, are cratered, barren, and utterly moonlike. The galaxy could contain a hundred billion planets that would be hard, at first glance, to distinguish from Mercury, and within our cosmic horizon, there are probably of order as many Mercury-like worlds as there are sucrose molecules in a cube of sugar.

Image Source.

Nevertheless, we do gain something extraordinary whenever a new vista onto a terrestrial world is opened up. Galileo was the first to achieve this, when he turned his telescope to the Moon and saw its three-dimensional relief for the first time. Mariner 4 and Mariner 9 accomplished a similar feat for Mars. The Magellan spacecraft revealed the Venusian topography. And once Messenger has photographed the full surface of Mercury, there will be a profoundly significant interval before we get our next up-close view of an unmapped terrestrial planet. My guess is that it’ll be Alpha Centauri B b.

The Messenger website is well worth a visit. I was particularly struck by the movie that the spacecraft made of the Earth during the close fly by of March 2005. During the course of 24 hours, the spinning Earth recedes into the black velvet distance and space travel seems like the real thing.

Mercury’s orbit, with its 88 day period and its eccentricity of 0.2 could slip unnoticed into the distribution of known exoplanets. It’s vaguely comparable, for example, with the orbit of HD 37605 b. This Msini=2.3 Mjup gas giant has an apoastron distance similar to Mercury’s, but dives much closer to its star during periastron.

We’ve been interested in HD 37605 b lately because its orbit dips in and out of the insolation zone where water clouds are expected to exist. At the far point of the 55 day orbit, it should be possible for white clouds to form out of a clear steamy atmosphere. At close approach, the clouds are turning to steam.

Jonathan Langton’s models for this planet show persistent polar vortices, which sequester cooler air, and which may remain cloudy even during the hot days surrounding periastron. The vortices are tenaciously long-lived, and tracer particles seeded into the vortices leak out only slowly. It would be interesting to know what sort of chemistry is brewing in the steamy hothouse environment of trapped and noxious air.

Sir, I have no need of that hypothesis!2
greg posted in worlds on January 15th, 2008

Image Source.

On the UCSC Science Library shelves, we have an 1828 edition of Pierre Simon de Laplace’s Oeuvres that includes the five-volume Mécanique Céleste. At moments like this, it’s great to have a camera on one’s cellphone:

Image Source.

Laplace’s identification of the 5:2 near-resonance between Jupiter and Saturn allowed him to augment the exisiting second-order Laplace-Lagrange secular analysis to produce a theory of planetary motion that was in extraordinary agreement with the observations of the late eighteenth century. His success in explaining the so-called Great Inequality was likely a contributing factor in the development the concept of Laplacian determinism, of a clockwork universe.

In 1802, during William Herschel’s visit to Paris, Herschel and Laplace had a meeting with Napoleon, who, like Thomas Jefferson, appears to have been not much taken with a system of the world created and dictated by natural law:

The first Consul then asked a few questions relating to Astronomy and the construction of the heavens to which I made such answers as seemed to give him great satisfaction. He also addressed himself to Mr. Laplace on the same subject, and held a considerable argument with him in which he differed from that eminent mathematician. The difference was occasioned by an exclamation of the first Consul, who asked in a tone of exclamation or admiration (when we were speaking of the extent of the sidereal heavens): ‘And who is the author of all this!’ Mons. De la Place wished to shew that a chain of natural causes would account for the construction and preservation of the wonderful system. This the first Consul rather opposed.

[Source: Herschel’s diary of his visit to Paris in 1802, as found in C. Lubbock’s _The Herschel Chronicle_, p. 310, see here for a nice background.]

I like the extrasolar planet game because it’s simultaneously up-to-the-minute and steeped in tradition. With systems like Gliese 876, we’re approaching roughly the same effective degree of refinement in our detection of planet-planet orbital perturbations that was possible in the late eighteenth century for Jupiter and Saturn. As a result, someone like Laplace, were he to materialize (see today’s NYT) in the Interdisciplinary Sciences Building here at UCSC, could roll up his french cuffs and immediately begin contributing publishable work. The same would certainly not be true if one of his equally luminous scientific contemporaries, say Antoine Lavoisier, were to suddenly walk in to a modern-day chemistry lab.

Will be making an effort to post more frequently. Thanks for your continued readership and participation as oklo.org heads into its third year.

6 Gigabytes. Two Stars. One Planet.6
greg posted in exoplanet detection, worlds on December 14th, 2007

Image Source.

Another long gap between posts. I’m starting to dig out from under my stack, however, and there’ll soon be some very interesting items to report.

As mentioned briefly in the previous post, our Spitzer observations of HD 80606 did indeed occur as scheduled. Approximately 7,800 8-micron 256×256 px IRAC images of the field containing HD 80606 and its binary companion HD 80607 were obtained during the 30-hour interval surrounding the periastron passage. On Nov. 22nd, the data (totaling a staggering 6 GB) was down-linked to the waiting Earth-based radio telescopes of NASA’s Deep Space Network. By Dec 4th, the data had cleared the Spitzer Science Center’s internal pipeline.

We’re living in a remarkable age. When I was in high school, I specifically remember standing out the backyard in the winter, scrutinizing the relatively sparse fields of stars in Ursa Major with my new 20×80 binoculars, and wondering whether any of them had planets. Now, a quarter century on, it’s possible to write and electronically submit a planetary observation proposal on a laptop computer, and then, less than a year later, 6 GB of data from a planet orbiting one of the stars visible in my binoculars literally rains down from the sky.

It will likely take a month or so before we’re finished with the analysis and the interpretation of the data. The IRAC instrument produces a gradually increasing sensitivity with time (known to the cognescenti as “the ramp”). This leads to a raw photometric light curve that slopes upward during the first hours of observation. For example, here’s the raw photometry from our Gliese 436 observations that Spitzer made last Summer. The ramp dominates the time series (although the secondary eclipse can also be seen):

The ramp differs in height, shape, and duration from case to case, but it is a well understood instrumental effect, and so its presence can be modeled out. Drake Deming is a world expert on this procedure, and so the data is in very capable hands. Once the ramp is gone, we’ll have a 2800-point 30 hour time series for both HD 80606 and HD 80607. We’ll be able to immediately see whether a secondary transit occurred (1 in 6.66 chance), and with more work, we’ll be able to measure how fast the atmosphere heats up during the periastron passage. Jonathan Langton is running a set of hydrodynamical simulations with different optical and infrared opacities, and we’ll be able to use these to get a full interpretation of the light curve.

In another exciting development, Joe Lazio, Paul Shankland, David Blank and collaborators were able to successfully observe HD 80606 using the VLA during the Nov. 19-20 periastron encounter! It’s not hard to imagine that there might be very interesting aurora-like effects that occur during the planet’s harrowing periastron passage. If so, the planet might have broadcasted significant power on the decameter band. Rest assured that when that when their analysis is ready, we’ll have all the details here at oklo.org.

55 Cancri - A tough nut to crack.5
greg posted in exoplanet detection, worlds on November 13th, 2007

Image Source.

As soon as the new data sets for 55 Cancri from the Keck and Lick Observatories were made public last week, they were added to the downloadable systemic console and to the systemic backend. The newly released radial velocities can be combined with existing published data from both ELODIE and HET.

Just as we’d hoped, the systemic backend users got right down to brass tacks. As anyone who has gone up against 55 Cnc knows, it is the Gangkhar Puensum of radial velocity data sets. There are four telescopes, hundreds of velocities, a nearly twenty year baseline, and a 2.8 day inner periodicity. Keplerian models, furthermore, can’t provide fully definitive fits to the data. Planet-planet gravitational perturbations need to be taken into account to fully resolve the system.

Eugenio has specified a number of different incarnations of the data set. It’s generally thought that fits to partial data sets will be useful for building up to a final definitive fit. Here’s a snapshot of the current situation on the backend:

The “55cancriup_4datasets” aggregate contains all of the published data for all four telescopes. This is therefore the dataset that is most in need of being fully understood. The best fit so far has been provided by Mike Hall, who submitted on Nov. 9th. After I wrote to congratulate him, he replied,

Thanks Greg, [...] It actually slipped into place very easily. About 13-30 minutes of adding planets and polishing with simple Keplerian, then 25 iterations overnight with Hermite 4th Order.

The problem is that it seemed like I was getting sucked into a very deep chi^2 minimum, so getting alternative fits may be tricky!

Here’s a detail from his fit which illustrates the degree of difference between the Keplerian and the full dynamical model:

and here’s a thumbnail of the inner configuration of the system. It’s basically a self-consistent version of the best 5-Keplerian fit.

Mike’s fit has a reduced chi-square of 7.72. This would require a Gaussian stellar jitter of 6.53 m/s in order to drop the reduced chi-square to unity. Yet 55 Cancri is an old, inherently quiet star, and so I think it’s possible, even likely, that there is still a considerable improvement to be had. It’s just not clear how to make the breakthrough happen.

This situation is thus what we’ve been hoping for all along with the systemic collaboration: A world-famous star, a high-quality highly complex published data set, a tough unsolved computational problem, and the promise of a fascinating dynamical insight if the problem can be solved.

I’ll end with two comments posted by the frontline crew (Eric Diaz, Mike Hall, Petej, and Chris Thiessen) that I found quite striking. These are part of a very interesting discussion that’s going on right now inside the backend.

When something is this difficult to solve using the ordinary approaches, I start to look to improbable and difficult solutions. In the case of 55C, my hunch is that it’s a system where the integration is necessary, but not sufficient to build a correct solution. I think that the parameter space of solutions is so chaotic that the L-M minimization doesn’t explore it well, or that the inclination of the system is significant enough to skew the planet-to-planet interactions in the console, or both. Trojans or horseshoe orbits would fit these conditions. Perhaps other resonant or eccentric orbits would as well.

I think the high chi square results and flat periodograms after fitting the known planets also point to a 1:1 resonant solution or significant inclination. I just don’t think there’s enough K left to fit another significant planet unless it’s highly interactive with the others.

I’m going to keep working on this system in the hopes that we can find a solution (and because it’s really, really fun), but I suspect that a satisfactory answer won’t be found without a systematic search of the parameter space including inclination.

– Chris

“Nature is not stranger than we imagine but stranger than we can imagine.” Or words to that effect, I can’t remember who said that but in all probability this system shall have more questions answered about it (or not as is often the case!) by direct imaging e.g. such as by the Terrestrial Planet Finder (TPF) mission to show what is really happening (if it is ever launched). The 55 Cancri system is listed as 63 on the top TPF 100 target stars.

In the meantime, we struggle on… I don’t think I can add anything else to what Eric and everyone else has said…

– Petej

Jonathan Langton’s new paper (available now!)1
greg posted in worlds on November 5th, 2007

Image Source.

The Spitzer telescope recently observed HAT-P-2b (data not yet analyzed) and the Nov. 19-20th encounter with HD 80606b is coming right up. No better time, then, to go out on a limb with our predictions of what will be seen. Our latest paper (Langton & Laughlin 2007) has been accepted by the Astrophysical Journal, and will be posted to astro-ph shortly. In the meantime, here’s a .pdf file containing the full paper. We’re happy with the way it came out, and we’re working hard to push the models to the next level.

From the conclusion:

A short-period Jovian planet on an eccentric orbit likely presents one of the Galaxy’s most thrilling sights. One can imagine, for example, how HD 86060 b appears during the interval surrounding its hair-rising encounter with its parent star. The blast of periastron heating drives global shock waves that reverberate several times around the globe. From Earth’s line of sight, the hours and days following periastron are characterized by a gradually dimming crescent of reflected starlight, accompanied by planet-wide vortical storms that fade like swirling embers as the planet recedes from the star. It’s remarkable that we now have the ability to watch this scene (albeit at one-pixel and two-frequency resolution) from a vantage several hundred light years away.